Presburger arithmetic
Encyclopedia
Presburger arithmetic is the first-order theory of the natural number
s with addition
, named in honor of Mojżesz Presburger
, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely. The axioms include a schema of induction.
Presburger arithmetic is much weaker than Peano arithmetic, which includes both addition and multiplication operations. Unlike Peano arithmetic, Presburger arithmetic is a decidable theory
. This means it is possible to effectively determine, for any sentence in the language of Presburger arithmetic, whether that sentence is provable from the axioms of Presburger arithmetic. The asymptotic running-time computational complexity
of this decision problem
is doubly exponential, however, as shown by Fischer and Rabin (1974).
(5) is an axiom schema
of induction
, representing infinitely many axioms. Since the axioms in the schema in (5) cannot be replaced by any finite number of axioms, Presburger arithmetic is not finitely axiomatizable.
Presburger arithmetic cannot formalize concepts such as divisibility or prime number
. Generally, any number concept leading to multiplication cannot be defined in Presburger arithmetic, since that leads to incompleteness and undecidability. However, it can formulate individual instances of divisibility; for example, it proves "for all x, there exists y : (y + y = x) ∨ (y + y + 1 = x)". This states that every number is either even or odd.
proved Presburger arithmetic to be:
The decidability of Presburger arithmetic can be shown using quantifier elimination
, supplemented by reasoning about arithmetical congruence (Enderton 2001, p. 188).
Peano arithmetic, which is Presburger arithmetic augmented with multiplication, cannot be decidable, as a consequence of the negative answer to the Entscheidungsproblem
. By Gödel's incompleteness theorem, Peano arithmetic is incomplete and its consistency is not internally provable.
The decision problem for Presburger arithmetic is an interesting example in computational complexity theory
and computation
. Let n be the length of a statement in Presburger arithmetic. Then Fischer and Rabin
(1974) proved that any decision algorithm for Presburger arithmetic has a worst-case runtime of at least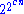
, for some constant c>0. Hence, the decision problem for Presburger arithmetic is an example of a decision problem that has been proved to require more than exponential run time. Fischer and Rabin also proved that for any reasonable axiomatization (defined precisely in their paper), there exist theorems of length n which have doubly exponential length proofs. Intuitively, this means there are computational limits on what can be proven by computer programs. Fischer and Rabin's work also implies that Presburger arithmetic can be used to define formulas which correctly calculate any algorithm as long as the inputs are less than relatively large bounds. The bounds can be increased, but only by using new formulas. On the other hand, a triply exponential upper bound on a decision procedure for Presburger Arithmetic was proved by Oppen (1978).
proof assistant system features a tactic for Presburger arithmetic.) The double exponential complexity of the theory makes it infeasible to use the theorem provers on complicated formulas, but this behavior occurs only in the presence of nested quantifiers: Oppen and Nelson (1980) describe an automatic theorem prover which uses the simplex algorithm
on an extended Presburger arithmetic without nested quantifiers. The simplex algorithm has exponential worst-case running time, but displays considerably better efficiency for typical real-life instances. Exponential running time is only observed for specially constructed cases. This makes a simplex-based approach practical in a working system.
Presburger arithmetic can be extended to include multiplication by constants, since multiplication is repeated addition. Most array subscript calculations then fall within the region of decidable problems. This approach is the basis of at least five proof of correctness systems for computer programs, beginning with the Stanford Pascal Verifier in the late 1970s and continuing though to Microsoft's Spec#
system of 2005.
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s with addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, named in honor of Mojżesz Presburger
Mojzesz Presburger
Mojżesz Presburger was a Polish Jewish mathematician, logician, and philosopher. He was a student of Alfred Tarski and is known for, among other things, having invented Presburger arithmetic as a student in 1929....
, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely. The axioms include a schema of induction.
Presburger arithmetic is much weaker than Peano arithmetic, which includes both addition and multiplication operations. Unlike Peano arithmetic, Presburger arithmetic is a decidable theory
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. This means it is possible to effectively determine, for any sentence in the language of Presburger arithmetic, whether that sentence is provable from the axioms of Presburger arithmetic. The asymptotic running-time computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of this decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
is doubly exponential, however, as shown by Fischer and Rabin (1974).
Overview
The language of Presburger arithmetic contains constants 0 and 1 and a binary function +, interpreted as addition. In this language, the axioms of Presburger arithmetic are the universal closures of the following:- ¬(0 = x + 1)
- x + 1 = y + 1 → x = y
- x + 0 = x
- (x + y) + 1 = x + (y + 1)
- Let P(x) be a first-order formulaFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
in the language of Presburger arithmetic with a free variable x (and possibly other free variables). Then the following formula is an axiom:
-
- (P(0) ∧ ∀x(P(x) → P(x + 1))) → P(y).
(5) is an axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, representing infinitely many axioms. Since the axioms in the schema in (5) cannot be replaced by any finite number of axioms, Presburger arithmetic is not finitely axiomatizable.
Presburger arithmetic cannot formalize concepts such as divisibility or prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Generally, any number concept leading to multiplication cannot be defined in Presburger arithmetic, since that leads to incompleteness and undecidability. However, it can formulate individual instances of divisibility; for example, it proves "for all x, there exists y : (y + y = x) ∨ (y + y + 1 = x)". This states that every number is either even or odd.
Properties
Mojżesz PresburgerMojzesz Presburger
Mojżesz Presburger was a Polish Jewish mathematician, logician, and philosopher. He was a student of Alfred Tarski and is known for, among other things, having invented Presburger arithmetic as a student in 1929....
proved Presburger arithmetic to be:
- consistentConsistency proofIn logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
: There is no statement in Presburger arithmetic which can be deduced from the axioms such that its negation can also be deduced. - completeCompletenessIn general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
: For each statement in Presburger arithmetic, either it is possible to deduce it from the axioms or it is possible to deduce its negation. - decidableDecidability (logic)In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
: There exists an algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which decides whether any given statement in Presburger arithmetic is true or false.
The decidability of Presburger arithmetic can be shown using quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
, supplemented by reasoning about arithmetical congruence (Enderton 2001, p. 188).
Peano arithmetic, which is Presburger arithmetic augmented with multiplication, cannot be decidable, as a consequence of the negative answer to the Entscheidungsproblem
Entscheidungsproblem
In mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...
. By Gödel's incompleteness theorem, Peano arithmetic is incomplete and its consistency is not internally provable.
The decision problem for Presburger arithmetic is an interesting example in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
and computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
. Let n be the length of a statement in Presburger arithmetic. Then Fischer and Rabin
Michael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
(1974) proved that any decision algorithm for Presburger arithmetic has a worst-case runtime of at least
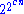, for some constant c>0. Hence, the decision problem for Presburger arithmetic is an example of a decision problem that has been proved to require more than exponential run time. Fischer and Rabin also proved that for any reasonable axiomatization (defined precisely in their paper), there exist theorems of length n which have doubly exponential length proofs. Intuitively, this means there are computational limits on what can be proven by computer programs. Fischer and Rabin's work also implies that Presburger arithmetic can be used to define formulas which correctly calculate any algorithm as long as the inputs are less than relatively large bounds. The bounds can be increased, but only by using new formulas. On the other hand, a triply exponential upper bound on a decision procedure for Presburger Arithmetic was proved by Oppen (1978).Applications
Because Presburger arithmetic is decidable, automatic theorem provers for Presburger arithmetic exist. (For example, the CoqCoq
In computer science, Coq is an interactive theorem prover. It allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification...
proof assistant system features a tactic for Presburger arithmetic.) The double exponential complexity of the theory makes it infeasible to use the theorem provers on complicated formulas, but this behavior occurs only in the presence of nested quantifiers: Oppen and Nelson (1980) describe an automatic theorem prover which uses the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
on an extended Presburger arithmetic without nested quantifiers. The simplex algorithm has exponential worst-case running time, but displays considerably better efficiency for typical real-life instances. Exponential running time is only observed for specially constructed cases. This makes a simplex-based approach practical in a working system.
Presburger arithmetic can be extended to include multiplication by constants, since multiplication is repeated addition. Most array subscript calculations then fall within the region of decidable problems. This approach is the basis of at least five proof of correctness systems for computer programs, beginning with the Stanford Pascal Verifier in the late 1970s and continuing though to Microsoft's Spec#
Spec sharp
Spec# is a programming language with specification language features that extends the capabilities of the C# programming language with Eiffel-like contracts, including object invariants, preconditions and postconditions. Like ESC/Java, it includes a static checking tool based on a theorem prover...
system of 2005.
External links
- online prover A Java applet proves or disproves arbitrary formulas of Presburger arithmetic (In German)
- http://www.philipp.ruemmer.org/princess.shtml A complete Theorem Prover for Presburger Arithmetic by Philipp Rümmer