Odd graph
Encyclopedia
In the mathematical
field of graph theory
, the odd graphs On are a family of symmetric graph
s with high odd girth, defined from certain set systems. They include and generalize the Petersen graph
.
KG(2n − 1,n − 1).
O2 is a triangle, while O3 is the familiar Petersen graph
.
The generalized odd graphs include the odd graphs and the folded cube graph
s, and are defined as distance-regular graph
s with diameter n − 1 and odd girth 2n − 1 for some n.
Odd graphs have been studied for their applications in chemical graph theory
, in modeling the shifts of carbonium ion
s. They have also been proposed as a network topology
in parallel computing
.
The notation On for these graphs was introduced by Norman Biggs in 1972. Biggs and Anthony Gardiner explain the name of odd graphs in an unpublished manuscript from 1974: each edge of an odd graph can be assigned the unique element of X which is the "odd man out
", i.e., not a member of either subset associated with the vertices incident to that edge.
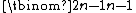vertices and 
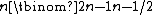edges. Therefore, the number of vertices for n = 1, 2,... is
Every odd graph is 3-arc-transitive
: every directed three-edge path in an odd graph can be transformed into every other such path by a symmetry of the graph.
Odd graphs are distance transitive
, hence distance regular
. As distance-regular graphs, they are uniquely defined by their intersection array: no other distance-regular graphs can have the same parameters as an odd graph. However, despite their high degree of symmetry, the odd graphs On for n > 2 are never Cayley graph
s.
Odd graphs with n ≥ 3 have girth six; however, although they are not bipartite graph
s, their odd cycles are much longer. Specifically, the odd graph On has odd girth 2n − 1. If a n-regular graph has diameter n − 1 and odd girth 2n − 1, and has only n distinct eigenvalues, it must be distance-regular. Distance-regular graphs with diameter n − 1 and odd girth 2n − 1 are known as the generalized odd graphs, and include the folded cube graph
s as well as the odd graphs themselves.
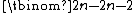vertices correspond to sets that contain x. Because all these sets contain x, they are not disjoint, and form an independent set
of On. That is, On has 2n − 1 different independent sets of size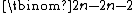
. It follows from the Erdős–Ko–Rado theorem
that these are the maximum independent sets of On. that is, the independence number of On is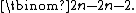
Further, every maximum independent set must have this form, so On has exactly 2n − 1 maximum independent sets.
If I is a maximum independent set, formed by the sets that contain x, then the complement
of I is the set of vertices that do not contain x. This complementary set induces a matching in G. Each vertex of the independent set is adjacent to n vertices of the matching, and each vertex of the matching is adjacent to n − 1 vertices of the independent set. Because of this decomposition, and because odd graphs are not bipartite, they have chromatic number three: the vertices of the maximum independent set can be assigned a single color, and two more colors suffice to color the complementary matching.
of the odd graph On is either n or n + 1, and in the case of the Petersen graph O3 it is n + 1. When n is a power of two, the number of vertices in the graph is odd, from which it again follows that the number of edge colors is n + 1. However, O5, O6, and O7 can each be edge-colored with n colors.
Biggs explains this problem with the following story: eleven soccer players in the fictional town of Croam wish to form up pairs of five-man teams
(with an odd man out to serve as referee) in all 1386 possible ways, and they wish to schedule the games between each pair in such a way that the six games for each team are played on six different days of the week, with Sundays off for all teams. Is it possible to do so? In this story, each game represents an edge of O6, each weekday is represented by a color, and a 6-color edge coloring of O6 provides a solution to the players' scheduling problem.
The Lovász conjecture
implies that every odd graph has a Hamiltonian path and that every odd graph On with n ≥ 4 has a Hamiltonian cycle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the odd graphs On are a family of symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
s with high odd girth, defined from certain set systems. They include and generalize the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
.
Definition and examples
The odd graph On has one vertex for each of the (n − 1)-element subsets of a (2n − 1)-element set. Two vertices are connected by an edge if and only if the corresponding subsets are disjoint. That is, On is a Kneser graphKneser graph
In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
KG(2n − 1,n − 1).
O2 is a triangle, while O3 is the familiar Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
.
The generalized odd graphs include the odd graphs and the folded cube graph
Folded cube graph
In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.-Construction:...
s, and are defined as distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
s with diameter n − 1 and odd girth 2n − 1 for some n.
History and applications
Although the Petersen graph has been known since 1898, its definition as an odd graph dates to the work of , who also studied the odd graph O4.Odd graphs have been studied for their applications in chemical graph theory
Chemical graph theory
Chemical graph theory is the topology branch of mathematical chemistry which applies graph theory to mathematical modelling of chemical phenomena....
, in modeling the shifts of carbonium ion
Carbonium ion
A carbonium ion is a carbocation of the penta- or tetracoordinated nonclassical type such as an ion of the type R5C+.- Methanium:The parent compound methanium or CH5+ is protonated methane and a superacid. This ion exists as a reactive intermediate in the interstellar medium and can be produced in...
s. They have also been proposed as a network topology
Network topology
Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....
in parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
.
The notation On for these graphs was introduced by Norman Biggs in 1972. Biggs and Anthony Gardiner explain the name of odd graphs in an unpublished manuscript from 1974: each edge of an odd graph can be assigned the unique element of X which is the "odd man out
Odd Man Out
Odd Man Out is a 1947 Anglo-Irish film noir directed by Carol Reed, starring James Mason, and is based on a novel of the same name by F. L. Green.-Plot:The film's opening intertitle reads:...
", i.e., not a member of either subset associated with the vertices incident to that edge.
Properties
The odd graph On is regular of degree n. It has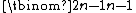 vertices and 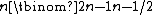edges. Therefore, the number of vertices for n = 1, 2,... is
- 1, 3, 10, 35, 126, 462, 1716, 6435 .
Distance and symmetry
If two vertices in On correspond to sets that differ from each other by the removal of k elements from one set and the addition of k different elements, then they may be reached from each other in 2k steps, each pair of which performs a single addition and removal. If 2k < n, this is a shortest path; otherwise, it is shorter to find a path of this type from the first set to a set complementary to the second, and then reach the second set in one more step. Therefore, the diameter of On is n − 1.Every odd graph is 3-arc-transitive
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
: every directed three-edge path in an odd graph can be transformed into every other such path by a symmetry of the graph.
Odd graphs are distance transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
, hence distance regular
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
. As distance-regular graphs, they are uniquely defined by their intersection array: no other distance-regular graphs can have the same parameters as an odd graph. However, despite their high degree of symmetry, the odd graphs On for n > 2 are never Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s.
Odd graphs with n ≥ 3 have girth six; however, although they are not bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s, their odd cycles are much longer. Specifically, the odd graph On has odd girth 2n − 1. If a n-regular graph has diameter n − 1 and odd girth 2n − 1, and has only n distinct eigenvalues, it must be distance-regular. Distance-regular graphs with diameter n − 1 and odd girth 2n − 1 are known as the generalized odd graphs, and include the folded cube graph
Folded cube graph
In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.-Construction:...
s as well as the odd graphs themselves.
Independent sets and vertex coloring
Let On be an odd graph defined from the subsets of a (2n − 1)-element set X, and let x be any member of X. Then, among the vertices of On, exactly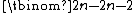 vertices correspond to sets that contain x. Because all these sets contain x, they are not disjoint, and form an independent setIndependent set
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
of On. That is, On has 2n − 1 different independent sets of size
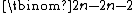. It follows from the Erdős–Ko–Rado theoremErdos–Ko–Rado theorem
In combinatorics, the Erdős–Ko–Rado theorem of Paul Erdős, Chao Ko, and Richard Rado is a theorem on hypergraphs, specifically, on uniform hypergraphs of rank r.The theorem is as follows...
that these are the maximum independent sets of On. that is, the independence number of On is
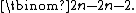Further, every maximum independent set must have this form, so On has exactly 2n − 1 maximum independent sets.If I is a maximum independent set, formed by the sets that contain x, then the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of I is the set of vertices that do not contain x. This complementary set induces a matching in G. Each vertex of the independent set is adjacent to n vertices of the matching, and each vertex of the matching is adjacent to n − 1 vertices of the independent set. Because of this decomposition, and because odd graphs are not bipartite, they have chromatic number three: the vertices of the maximum independent set can be assigned a single color, and two more colors suffice to color the complementary matching.
Edge coloring
By Vizing's theorem, the number of colors needed to color the edgesEdge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
of the odd graph On is either n or n + 1, and in the case of the Petersen graph O3 it is n + 1. When n is a power of two, the number of vertices in the graph is odd, from which it again follows that the number of edge colors is n + 1. However, O5, O6, and O7 can each be edge-colored with n colors.
Biggs explains this problem with the following story: eleven soccer players in the fictional town of Croam wish to form up pairs of five-man teams
Five-a-side football
thumb|240px|alt=Men playing football on artificial grass pitch.|Five-a-side game on astroturf pitch.Five-a-side football is a variation of association football in which each team fields five players , rather than the usual eleven on each team. Other differences from football include a smaller...
(with an odd man out to serve as referee) in all 1386 possible ways, and they wish to schedule the games between each pair in such a way that the six games for each team are played on six different days of the week, with Sundays off for all teams. Is it possible to do so? In this story, each game represents an edge of O6, each weekday is represented by a color, and a 6-color edge coloring of O6 provides a solution to the players' scheduling problem.
Hamiltonicity
The Petersen graph O3 is a well known non-Hamiltonian graph, but O4 through O14 have been shown to contain Hamiltonian cycles. More strongly, combining the Hamiltonian cycle and edge coloring problems, it is possible to partition the edges of On (for n = 4, 5, 6, 7) into floor(n/2) Hamiltonian cycles; when n is odd, the leftover edges form a perfect matching. For n = 8, the odd number of vertices in On prevents an 8-color edge coloring from existing, but does not rule out the possibility of a partition into four Hamiltonian cycles.The Lovász conjecture
Lovász conjecture
In graph theory, the Lovász conjecture is a classical problem on Hamiltonian paths in graphs. It says:The original article of Lovász stated the result in the opposite, butthis version became standard...
implies that every odd graph has a Hamiltonian path and that every odd graph On with n ≥ 4 has a Hamiltonian cycle.