Object theory
Encyclopedia
Object theory is a theory in philosophy
and mathematical logic
concerning objects and the statements that can be made about objects.
in classical mathematics can be regarded as a simple and elegant systematizing scheme, by which a variety of (presumably) true real statements, previously appearing as heterogeneous and unrelated, and often previously unknown, are comprised as consequences of the ideal theorems in the theory... ." (Kleene 1952:57 quoting von Neumann 1947, Einstein 1944)
A further specification of the objects results in a model or representation of the abstract system, "i.e. a system of objects which satisfy the relationships of the abstract system and have some further status as well" (ibid).
A model of this little system would occur when we assign, for example the familiar natural numbers { 0, 1, 2, 3 }, to the symbols { ←, ↑, →, ↓ }, i.e. in this manner: → = 0, ↑ = 1, ← = 2, ↓ = 3 . Here, the symbol ∫ indicates the "successor function" (often written as an apostrophe ' to distinguish it from +) operating on a collection of only 4 objects, thus 0' = 1, 1' = 2, 2' = 3, 3' = 0.
Unlike the ∫ example above, the following creates an unbounded number of objects. The fact that O is a set, and □ is an element of O, and ■ is an operation, must be specified at the outset; this is being done in the language of the metatheory
(see below):
Kurt Godel 1931 virtually constructed the entire proof of his incompleteness theorems (actually he proved Theorem IV and sketched a proof of Theorem XI) by use of this tactic, proceeding from his axioms using substitution, concatenation and deduction of modus ponens to produce a collection of 45 "definitions" (derivations or theorems more accurately) from the axioms.
A more familiar tactic is perhaps the design of subroutines that are given names, e.g. in Excel the subroutine " =INT(A1)" that returns to the cell where it is typed (e.g. cell B1) the integer it finds in cell A1.
tape with its fixed "head" located on the left-end square; the system's relation is equivalent to: "To the left end, tack on a new square □, right-shift the tape, then print ■ on the new square". Another model is the natural numbers as created by the "successor" function. Because the objects in the two systems e.g. ( □, ■□, ■■□, ■■■□ ... ) and (0, 0', 0, 0, ...) can be put into a 1-1 correspondence, the systems are said to be (simply) isomorphic (meaning "same shape"). Yet another isomorphic model is the little sequence of instructions for a counter machine
e.g. "Do the following in sequence: (1) Dig a hole. (2) Into the hole, throw a pebble. (3) Go to step 2."
As long as their objects can be placed in one-to-one correspondence ("while preserving the relationships") models can be considered "equivalent" no matter how their objects are generated (e.g. genetically or axiomatically):
Once the step has been taken to write down the symbols 3 2 1 0 one after another on a piece of paper (writing the new symbol on the left this time), or writing ∫∫∫※∫∫※∫※※ in a similar manner, then putting them in 1-1 correspondence with the Turing-tape symbols seems obvious. Digging holes one after the other, starting with a hole at "the origin", then a hole to its left with one pebble in it, then a hole to its left with two pebbles in it, ad infinitum, raises practical questions, but in the abstract it too can be seen to be conducive to the same 1-1 correspondence.
However, nothing in particular in the definition of genetic versus axiomatic methods clears this up—these are issues to be discussed in the metatheory. The mathematician or scientist is to be held responsible for sloppy specifications. Breger cautions that axiomatic methods are susceptible to tacit knowledge, in particular, the sort that involves "know-how of a human being" (Breger 2000:227).
or "formal theory" consists of "objects" in a structure:
exists outside the formalized object theory—the meaningless symbols and relations and (well-formed-) strings of symbols. The metatheory comments on (describes, interprets, illustrates) these meaningless objects using "intuitive" notions and "ordinary language". Like the object theory, the metatheory should be disciplined, perhaps even quasi-formal itself, but in general the interpretations of objects and rules are intuitive rather than formal. Kleene requires that the methods of a metatheory (at least for the purposes of metamathematics
) be finite, conceivable, and performable; these methods cannot appeal to the completed infinite. "Proofs of existence shall give, at least implicitly, a method for constructing the object which is being proved to exist." (p. 64)
Kleene summarizes this as follows: "In the full picture there will be three separate and distinct "theories""
He goes on to say that object theory (b) is not a "theory" in the conventional sense, but rather is "a system of symbols and of objects built from symbols (described from (c))".
). This algorithm, in the extreme, might require (or be) a Turing machine
or Turing-equivalent machine that "parses" the symbol-string as presented as "data" on its tape; before a universal Turing machine
can execute an instruction on its tape, it must parse the symbols to determine the exact nature of the instruction and/or datum encoded there. In simpler cases a finite state machine
or a pushdown automaton
can do the job. Enderton describes the use of "trees" to determine whether or not a logic formula (in particular a string of symbols with parentheses) is well formed. Alonzo Church
1934 describes the construction of "formulas" (again: sequences of symbols) as written in his λ-calculus by use of a recursive
description of how to start a formula and then build on the starting-symbol using concatenation and substitution.
Example: Church specified his λ-calculus as follows (the following is simplified version leaving out notions of free- and bound-variable). This example shows how an object theory begins with a specification of an object system of symbols and relations (in particular by use of concatenation of symbols):
Declare the symbols: {, }, , λ, [, ] plus an infinite number of variables a, b, c, ..., x, ...
Define formula: a sequence of symbols
Define the notion of "well-formed formula" (wff) recursively starting with the "basis" (3.i):
Define various abbreviations:
Define the notion of "substitution" of formula N for variable x throughout M (Church 1936)
In the next example, the undefined symbols will be { ※, ↀ, ∫ }. The axioms will describe their behaviors.
After (i) a definition of "string S" -- an object that is a symbol ※ or concatenated symbols ※, ↀ or ∫, and (ii) a definition of "well-formed" strings -- (basis) ※ and ↀS, ∫S where S is any string, come the axioms:
So what might be the (intended) interpretation of these symbols, definitions, and axioms?
If we define ※ as "0", ∫ as "successor", and ↀ as "predecessor" then ↀ※ => ※ indicates "proper subtraction" (sometimes designated by the symbol ∸, where "predecessor" subtracts a unit from a number, thus 0 ∸1 = 0). The string " ↀ∫n => n " indicates that if first the successor is applied to an arbitrary object n and then the predecessor ↀ is applied to ∫n, the original n results."
Is this set of axioms "adequate"? The proper answer would be a question: "Adequate to describe what, in particular?" "The axioms determine to which systems, defined from outside the theory, the theory applies." (Kleene 1952:27). In other words, the axioms may be sufficient for one system but not for another.
In fact, it is easy to see that this axiom set is not a very good one—in fact, it is inconsistent (that is, it yields inconsistent outcomes, no matter what its interpretation):
Observe also that the axiom set does not specify that ∫n ≠ n. Or, excepting the case n = ※, ↀn ≠ n. If we were to include these two axioms we would need to describe the intuitive notions "equals" symbolized by = and not-equals symbolized by ≠.
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
concerning objects and the statements that can be made about objects.
An informal theory
"A theoryTheory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
in classical mathematics can be regarded as a simple and elegant systematizing scheme, by which a variety of (presumably) true real statements, previously appearing as heterogeneous and unrelated, and often previously unknown, are comprised as consequences of the ideal theorems in the theory... ." (Kleene 1952:57 quoting von Neumann 1947, Einstein 1944)
Objects
In some cases "objects" can be concretely thought of as symbols and strings of symbols, here illustrated by a string of four symbols " ←←↑↓←→←↓" as composed from the 4-symbol alphabet { ←, ↑, →, ↓ } . When they are "known only through the relationships of the system [in which they appear], the system is [said to be] abstract ... what the objects are, in any respect other than how they fit into the structure, is left unspecified." (Kleene 1952:25)A further specification of the objects results in a model or representation of the abstract system, "i.e. a system of objects which satisfy the relationships of the abstract system and have some further status as well" (ibid).
A system
A system, in its general sense, is a collection of objects O = {o1, o2, ... on, ... } and (a specification of) the relationship r or relationships r1, r2, ... rn between the objects:- Example: Given a simple system = { { ←, ↑, →, ↓ }, ∫ } for a very simple relationship between the objects as signified by the symbol ∫ :
- ∫→ => ↑, ∫↑ => ←, ∫← => ↓, ∫↓ => →
A model of this little system would occur when we assign, for example the familiar natural numbers { 0, 1, 2, 3 }, to the symbols { ←, ↑, →, ↓ }, i.e. in this manner: → = 0, ↑ = 1, ← = 2, ↓ = 3 . Here, the symbol ∫ indicates the "successor function" (often written as an apostrophe ' to distinguish it from +) operating on a collection of only 4 objects, thus 0' = 1, 1' = 2, 2' = 3, 3' = 0.
- Or, we might specify that ∫ represents 90-degree counter-clockwise rotations of a simple object → .
The genetic versus axiomatic method
The following is an example of the genetic or constructive method of making objects in a system, the other being the axiomatic or postulational method. Kleene states that a genetic method is intended to "generate" all the objects of the system and thereby "determine the abstract structure of the system completely" and uniquely (and thus define the system categorically). If axioms rather than a genetic method is used, such axiom-sets are said to be categorical.Unlike the ∫ example above, the following creates an unbounded number of objects. The fact that O is a set, and □ is an element of O, and ■ is an operation, must be specified at the outset; this is being done in the language of the metatheory
Metatheory
A metatheory or meta-theory is a theory whose subject matter is some other theory. In other words it is a theory about a theory. Statements made in the metatheory about the theory are called metatheorems....
(see below):
- Given the system ( O, □, ■ ): O = { □, ■□, ■■□, ■■■□, ■■■■□, ■■■■■□, ..., ■n□, etc. }
Abbreviations
The object ■n□ demonstrates the use of "abbreviation", a way to simplify the denoting of objects, and consequently discussions about them, once they have been created "officially". Done correctly the definition would proceed as follows:-
-
- ■□ ≡ ■1□, ■■□ ≡ ■2□, ■■■□ ≡ ■3□, etc, where the notions of ≡ ("defined as") and "number" are presupposed to be understood intuitively in the metatheory.
-
Kurt Godel 1931 virtually constructed the entire proof of his incompleteness theorems (actually he proved Theorem IV and sketched a proof of Theorem XI) by use of this tactic, proceeding from his axioms using substitution, concatenation and deduction of modus ponens to produce a collection of 45 "definitions" (derivations or theorems more accurately) from the axioms.
A more familiar tactic is perhaps the design of subroutines that are given names, e.g. in Excel the subroutine " =INT(A1)" that returns to the cell where it is typed (e.g. cell B1) the integer it finds in cell A1.
Models
A model of the above example is a left-ended Post-Turing machinePost-Turing machine
A Post–Turing machine is a "program formulation" of an especially simple type of Turing machine, comprising a variant of Emil Post's Turing-equivalent model of computation described below. A Post–Turing machine is a "program formulation" of an especially simple type of Turing machine, comprising a...
tape with its fixed "head" located on the left-end square; the system's relation is equivalent to: "To the left end, tack on a new square □, right-shift the tape, then print ■ on the new square". Another model is the natural numbers as created by the "successor" function. Because the objects in the two systems e.g. ( □, ■□, ■■□, ■■■□ ... ) and (0, 0', 0, 0, ...) can be put into a 1-1 correspondence, the systems are said to be (simply) isomorphic (meaning "same shape"). Yet another isomorphic model is the little sequence of instructions for a counter machine
Counter machine
A counter machine is an abstract machine used in formal logic and theoretical computer science to model computation. It is the most primitive of the four types of register machines...
e.g. "Do the following in sequence: (1) Dig a hole. (2) Into the hole, throw a pebble. (3) Go to step 2."
As long as their objects can be placed in one-to-one correspondence ("while preserving the relationships") models can be considered "equivalent" no matter how their objects are generated (e.g. genetically or axiomatically):
- "Any two simply isomorphic systems constitute representations [models] of the same abstract system, which is obtained by abstracting from either of them, i.e. by leaving out of account all relationships and properties except the ones to be considered for the abstract system." (Kleene 1935:25)
Tacit assumptions, tacit knowledge
An alert reader may have noticed that writing symbols □, ■□, ■■□, ■■■□, etc. by concatenating a marked square, i.e. ■, to an existing string is different than writing the completed symbols one after another on a Turing-machine tape. Another entirely possible scenario would be to generate the symbol-strings one after another on different sections of tape e.g. after three symbols: ■■■□■■□■□□. The proof that these two possibilities are different is easy: they require different "programs". But in a sense both versions create the same objects; in the second case the objects are preserved on the tape. In the same way, if a person were to write 0, then erase it, write 1 in the same place, then erase it, write 2, erase it, ad infinitum, the person is generating the same objects as if they were writing down 0 1 2 3 ... writing one symbol after another to the right on the paper.Once the step has been taken to write down the symbols 3 2 1 0 one after another on a piece of paper (writing the new symbol on the left this time), or writing ∫∫∫※∫∫※∫※※ in a similar manner, then putting them in 1-1 correspondence with the Turing-tape symbols seems obvious. Digging holes one after the other, starting with a hole at "the origin", then a hole to its left with one pebble in it, then a hole to its left with two pebbles in it, ad infinitum, raises practical questions, but in the abstract it too can be seen to be conducive to the same 1-1 correspondence.
However, nothing in particular in the definition of genetic versus axiomatic methods clears this up—these are issues to be discussed in the metatheory. The mathematician or scientist is to be held responsible for sloppy specifications. Breger cautions that axiomatic methods are susceptible to tacit knowledge, in particular, the sort that involves "know-how of a human being" (Breger 2000:227).
A formal system
In general, in mathematics a formal systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
or "formal theory" consists of "objects" in a structure:
- The symbols to be concatenated (adjoined),
- The formation-rules (completely specified, i.e. formal rules of syntaxSyntaxIn linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
) that dictate how the symbols and the assemblies of symbols are to be formed into assemblies (e.g. sequences) of symbols (called terms, formulas, sentences, propositions, theorems, etc) so that they are in "well-formed" patterns (e.g. can a symbol be concatenated at its left end only, at its right end only, or both ends simultaneously? Can a collection of symbols be substituted for (put in place of) one or more symbols that may appear anywhere in the target symbol-string?), - Well-formed "propositions" (called "theorems" or assertions or sentences) assembled per the formation rules,
- A few axiomAxiomIn traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s that are stated up front and may include "undefinable notions" (examples: "set", "element", "belonging" in set theory; "0" and " ' " (successor) in number theory), - At least one rule of deductive inference (e.g. modus ponensModus ponensIn classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
) that allow one to pass from one or more of the axioms and/or propositions to another proposition.
Informal theory, object theory, and metatheory
A metatheoryMetatheory
A metatheory or meta-theory is a theory whose subject matter is some other theory. In other words it is a theory about a theory. Statements made in the metatheory about the theory are called metatheorems....
exists outside the formalized object theory—the meaningless symbols and relations and (well-formed-) strings of symbols. The metatheory comments on (describes, interprets, illustrates) these meaningless objects using "intuitive" notions and "ordinary language". Like the object theory, the metatheory should be disciplined, perhaps even quasi-formal itself, but in general the interpretations of objects and rules are intuitive rather than formal. Kleene requires that the methods of a metatheory (at least for the purposes of metamathematics
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
) be finite, conceivable, and performable; these methods cannot appeal to the completed infinite. "Proofs of existence shall give, at least implicitly, a method for constructing the object which is being proved to exist." (p. 64)
Kleene summarizes this as follows: "In the full picture there will be three separate and distinct "theories""
- "(a) the informal theory of which the formal system constitutes a formalization
- "(b) the formal system or object theory, and
- "(c) the metatheory, in which the formal system is described and studied" (p. 65)
He goes on to say that object theory (b) is not a "theory" in the conventional sense, but rather is "a system of symbols and of objects built from symbols (described from (c))".
Well-formed objects
If a collection of objects (symbols and symbol-sequences) is to be considered "well-formed", an algorithm must exist to determine, by halting with a "yes" or "no" answer, whether or not the object is well-formed (in mathematics a wff abbreviates well-formed formulaWell-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
). This algorithm, in the extreme, might require (or be) a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
or Turing-equivalent machine that "parses" the symbol-string as presented as "data" on its tape; before a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
can execute an instruction on its tape, it must parse the symbols to determine the exact nature of the instruction and/or datum encoded there. In simpler cases a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
or a pushdown automaton
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
can do the job. Enderton describes the use of "trees" to determine whether or not a logic formula (in particular a string of symbols with parentheses) is well formed. Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
1934 describes the construction of "formulas" (again: sequences of symbols) as written in his λ-calculus by use of a recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
description of how to start a formula and then build on the starting-symbol using concatenation and substitution.
Example: Church specified his λ-calculus as follows (the following is simplified version leaving out notions of free- and bound-variable). This example shows how an object theory begins with a specification of an object system of symbols and relations (in particular by use of concatenation of symbols):
Declare the symbols: {, }, , λ, [, ] plus an infinite number of variables a, b, c, ..., x, ...
Define formula: a sequence of symbols
Define the notion of "well-formed formula" (wff) recursively starting with the "basis" (3.i):
- (3.1) (basis) A variable x is a wff
- (3.2) If F and X are wffs, then {F}(X) is a wff; if x occurs in F or X then it is said to be a variable in {F}(X).
- (3.3) If M is well-formed and x occurs in M then λx[M] is a wff.
Define various abbreviations:
- {F}[X] abbreviates to F(X) if F is a single symbol
-
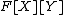abbreviates to {F}(X,Y) or F(X,Y) if F is a single symbol - λx1λx2[...λxn[M]...] abbreviates to λx1x2...xn•M
- λab•a(b) abbreviates to 1
- λab•a(a(b)) abbreviates to 2, etc.
Define the notion of "substitution" of formula N for variable x throughout M (Church 1936)
Undefined (primitive) objects
Certain objects may be "undefined" or "primitive" and receive definition (in the terms of their behaviors) by the introduction of the axioms.In the next example, the undefined symbols will be { ※, ↀ, ∫ }. The axioms will describe their behaviors.
Axioms
Kleene observes that the axioms are made up of two sets of symbols: (i) the undefined or primitive objects and those that are previously known. In the following example, it is previously known in the following system ( O, ※, ↀ, ∫ ) that O constitutes a set of objects (the "domain"), ※ is an object in the domain, ↀ and ∫ are symbols for relations between the objects, => indicates the "IF THEN" logical operator, ε is the symbol that indicates "is an element of the set O", and "n" will be used to indicate an arbitrary element of set-of-objects O.After (i) a definition of "string S" -- an object that is a symbol ※ or concatenated symbols ※, ↀ or ∫, and (ii) a definition of "well-formed" strings -- (basis) ※ and ↀS, ∫S where S is any string, come the axioms:
- ↀ※ => ※, in words: "IF ↀ is applied to object ※ THEN object ※ results."
- ∫n ε O, in words "IF ∫ is applied to arbitrary object "n" in O THEN this object ∫n is an element of O".
- ↀn ε O, "IF ↀ is applied to arbitrary object "n" in O THEN this object ↀn is an element of O".
- ↀ∫n => n, "IF ↀ is applied to object ∫n THEN object n results."
- ∫ↀn => n, "IF ∫ is applied to object ↀn THEN object ※ results."
So what might be the (intended) interpretation of these symbols, definitions, and axioms?
If we define ※ as "0", ∫ as "successor", and ↀ as "predecessor" then ↀ※ => ※ indicates "proper subtraction" (sometimes designated by the symbol ∸, where "predecessor" subtracts a unit from a number, thus 0 ∸1 = 0). The string " ↀ∫n => n " indicates that if first the successor is applied to an arbitrary object n and then the predecessor ↀ is applied to ∫n, the original n results."
Is this set of axioms "adequate"? The proper answer would be a question: "Adequate to describe what, in particular?" "The axioms determine to which systems, defined from outside the theory, the theory applies." (Kleene 1952:27). In other words, the axioms may be sufficient for one system but not for another.
In fact, it is easy to see that this axiom set is not a very good one—in fact, it is inconsistent (that is, it yields inconsistent outcomes, no matter what its interpretation):
- Example: Define ※ as 0, ∫※ as 1, and ↀ1 = 0. From the first axiom, ↀ※ = 0, so ∫ↀ※ = ∫0 = 1. But the last axiom specifies that for any arbitrary n including ※ = 0, ∫ↀn => n, so this axiom stipulates that ∫ↀ0 => 0, not 1.
Observe also that the axiom set does not specify that ∫n ≠ n. Or, excepting the case n = ※, ↀn ≠ n. If we were to include these two axioms we would need to describe the intuitive notions "equals" symbolized by = and not-equals symbolized by ≠.
External links
- The Theory of Abstract Objects at the Stanford Metaphysical Research Lab.