Normalization (statistics)
Encyclopedia
In one usage in statistics
, normalization is the process of isolating statistical error
in repeated measured data. A normalization is sometimes based on a property. Quantile normalization
, for instance, is normalization based on the magnitude (quantile
) of the measures.
In another usage in statistics, normalization refers to the division of multiple sets of data by a common variable in order to negate that variable's effect on the data, thus allowing underlying characteristics of the data sets to be compared: this allows data on different scales to be compared, by bringing them to a common scale. In terms of levels of measurement, these ratios only make sense for ratio measurements (where ratios of measurements are meaningful), not interval measurements (where only distances are meaningful, but not ratios).
Parametric normalization frequently uses pivotal quantities
– functions whose sampling distribution
does not depend on the parameters – and particularly ancillary statistic
s – pivotal quantities that can be computed from observations, without knowing parameters.
Note that some other ratios, such as the variance-to-mean ratio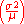
, are also done for normalization, but are not nondimensional: the units do not cancel, and thus the ratio has units, and are not scale invariant.
data to enable differentiation between real (biological) variations in gene expression levels and variations due to the measurement process.
In microarray
analysis, normalization refers to the process of identifying and removing the systematic effects, and bringing the data from different microarrays onto a common scale.
, combining images to a common scale is called image registration
, in the sense of "aligning different images". For example, stitching together images in a panorama or combining pictures from different angles.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, normalization is the process of isolating statistical error
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
in repeated measured data. A normalization is sometimes based on a property. Quantile normalization
Quantile normalization
In statistics, quantile normalization is a technique for making two distributions identical in statistical properties. To quantile-normalize a test distribution to a reference distribution of the same length, sort the test distribution and sort the reference distribution...
, for instance, is normalization based on the magnitude (quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
) of the measures.
In another usage in statistics, normalization refers to the division of multiple sets of data by a common variable in order to negate that variable's effect on the data, thus allowing underlying characteristics of the data sets to be compared: this allows data on different scales to be compared, by bringing them to a common scale. In terms of levels of measurement, these ratios only make sense for ratio measurements (where ratios of measurements are meaningful), not interval measurements (where only distances are meaningful, but not ratios).
Parametric normalization frequently uses pivotal quantities
Pivotal quantity
In statistics, a pivotal quantity or pivot is a function of observations and unobservable parameters whose probability distribution does not depend on unknown parameters....
– functions whose sampling distribution
Sampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
does not depend on the parameters – and particularly ancillary statistic
Ancillary statistic
In statistics, an ancillary statistic is a statistic whose sampling distribution does not depend on which of the probability distributions among those being considered is the distribution of the statistical population from which the data were taken...
s – pivotal quantities that can be computed from observations, without knowing parameters.
Examples
There are various normalizations in statistics – nondimensional ratios of errors, residuals, means and standard deviations, which are hence scale invariant – some of which may be summarized as follows. Note that in terms of levels of measurement, these ratios only make sense for ratio measurements (where ratios of measurements are meaningful), not interval measurements (where only distances are meaningful, but not ratios). See also :Category:Statistical ratios.| Name | Formula | Use |
|---|---|---|
| Standard score Standard score In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation... |
 |
Normalizing errors when population parameters are known. |
| Student's t-statistic Student's t-statistic In statistics, the t-statistic is a ratio of the departure of an estimated parameter from its notional value and its standard error. It is used in hypothesis testing, for example in the Student's t-test, in the augmented Dickey–Fuller test, and in bootstrapping.-Definition:Let \scriptstyle\hat\beta... |
 |
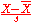Normalizing residuals when population parameters are unknown (estimated). |
| Studentized residual Studentized residual In statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard... |
 |
Normalizing residuals when parameters are estimated, particularly across different data points in regression analysis Regression analysis In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables... . |
| Standardized moment |  |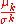
Normalizing moments, using the standard deviation  as a measure of scale. |
| Coefficient of variation Coefficient of variation In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is... |
 |
Normalizing dispersion, using the mean  as a measure of scale, particularly for positive distribution such as the exponential distributionExponential distribution In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e... and Poisson distribution Poisson distribution In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since... . |
Note that some other ratios, such as the variance-to-mean ratio
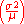, are also done for normalization, but are not nondimensional: the units do not cancel, and thus the ratio has units, and are not scale invariant.Applications
In an experimental context, normalizations are used to standardise microarrayDNA microarray
A DNA microarray is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome...
data to enable differentiation between real (biological) variations in gene expression levels and variations due to the measurement process.
In microarray
DNA microarray
A DNA microarray is a collection of microscopic DNA spots attached to a solid surface. Scientists use DNA microarrays to measure the expression levels of large numbers of genes simultaneously or to genotype multiple regions of a genome...
analysis, normalization refers to the process of identifying and removing the systematic effects, and bringing the data from different microarrays onto a common scale.
Related processes
In computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, combining images to a common scale is called image registration
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
, in the sense of "aligning different images". For example, stitching together images in a panorama or combining pictures from different angles.
Examples
- Standard scoreStandard scoreIn statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...
- Studentized residualStudentized residualIn statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...
- Standardized moment,
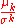
- Coefficient of variationCoefficient of variationIn probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
,
Analogs
- Image registrationImage registrationImage registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
, moving data in computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
to a common scale - NondimensionalizationNondimensionalizationNondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
in physics