
Quantile
Encyclopedia
Quantiles are points taken at regular intervals from the cumulative distribution function
(CDF) of a random variable
. Dividing ordered data into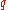 essentially equal-sized data subsets is the motivation for
essentially equal-sized data subsets is the motivation for 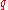 -quantiles; the quantiles are the data values marking the boundaries between consecutive subsets. Put another way, the
-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets. Put another way, the 
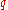 -quantile for a random variable is the value
-quantile for a random variable is the value  such that the probability that the random variable will be less than
such that the probability that the random variable will be less than  is at most
is at most 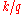 and the probability that the random variable will be more than
and the probability that the random variable will be more than  is at most
is at most  . There are
. There are 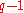 of the
of the 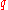 -quantiles, one for each integer
-quantiles, one for each integer 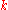 satisfying
satisfying 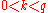 .
.
More generally, one can consider the quantile function
for any distribution. This is defined for real variables between zero and one and is mathematically the inverse of the cumulative distribution function.
 th
th 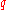 -quantile is the data value where the cumulative distribution function crosses
-quantile is the data value where the cumulative distribution function crosses 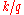 . That
. That  is a
is a 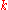 th
th  -quantile for a variable
-quantile for a variable  if
if
and
For a finite population of values indexed 1,...,
values indexed 1,..., from lowest to highest, the
from lowest to highest, the 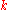 th
th 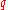 -quantile of this population can be computed via the value of
-quantile of this population can be computed via the value of 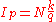 . If
. If 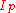 is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the
is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the 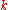 th
th 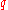 -quantile. On the other hand, if
-quantile. On the other hand, if 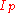 is an integer then any number from the data value at that index to the data value of the next can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating the quantiles).
is an integer then any number from the data value at that index to the data value of the next can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating the quantiles).
If, instead of using integers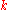 and
and  , the “
, the “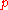 -quantile” is based on a real number
-quantile” is based on a real number
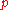 with
with 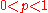 , then
, then  replaces
replaces 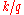 in the above formulae. Some software programs (including Microsoft Excel
in the above formulae. Some software programs (including Microsoft Excel
) regard the minimum and maximum as the 0th and 100th percentile, respectively; however, such terminology is an extension beyond traditional statistics definitions.
If a distribution is symmetric, then the median is the mean (so long as the latter exists). But, in general, the median and the mean differ. For instance, with a random variable that has an exponential distribution
, any particular sample of this random variable will have roughly a 63% chance of being less than the mean. This is because the exponential distribution has a long tail for positive values but is zero for negative numbers.
Quantiles are useful measures because they are less susceptible to long-tailed distributions and outliers. Empirically, if the data being analyzed are not actually distributed according to an assumed distribution, or if there are other potential sources for outliers that are far removed from the mean, then quantiles may be more useful descriptive statistics than means and other moment-related statistics.
Closely related is the subject of least absolute deviations
, a method of regression that is more robust to outliers than is least squares, in which the sum of the absolute value of the observed errors is used in place of the squared error. The connection is that the mean is the single estimate of a distribution that minimizes expected squared error while the median minimizes expected absolute error. Least absolute deviations
shares the ability to be relatively insensitive to large deviations in outlying observations, although even better methods of robust regression
are available.
The quantiles of a random variable are preserved under increasing transformations, in the sense that, for example, if is the median of a random variable
is the median of a random variable  , then
, then  is the median of
is the median of 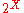 , unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, below, for examples of such interpolation.) Quantiles can also be used in cases where only ordinal
, unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, below, for examples of such interpolation.) Quantiles can also be used in cases where only ordinal
data are available.
the quantiles. The most comprehensive breadth of methods is available in the R programming language
, which includes nine sample quantile methods. SAS includes five sample quantile methods, STATA
includes two, and Microsoft Excel
includes one.
In effect, the methods compute Qp, the estimate for the kth q-quantile, where p = k / q, from a sample of size N by computing a real valued index h. When h is an integer, the hth smallest of the N values, xh, is the quantile estimate. Otherwise a rounding or interpolation scheme is used to compute the quantile estimate from h, x⌊h⌋, and x⌈h⌉. (For notation, see floor and ceiling functions).
Estimate types include:
Note that R-3 and R-4 do not give h = (N + 1) / 2 when p = 1/2.
Monte Carlo simulations show that method R-5 is the preferred method for continuous data.
The standard error
of a quantile estimate can in general be estimated via the bootstrap. The Maritz-Jarrett method can also be used. Note that a Bayesian approach to quantile estimation (along with a credible interval
) fails with an improper prior and a proper prior is required.
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(CDF) of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. Dividing ordered data into
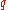 essentially equal-sized data subsets is the motivation for
essentially equal-sized data subsets is the motivation for 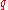 -quantiles; the quantiles are the data values marking the boundaries between consecutive subsets. Put another way, the
-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets. Put another way, the 
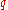 -quantile for a random variable is the value
-quantile for a random variable is the value  such that the probability that the random variable will be less than
such that the probability that the random variable will be less than  is at most
is at most 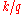 and the probability that the random variable will be more than
and the probability that the random variable will be more than  is at most
is at most  . There are
. There are 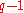 of the
of the 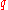 -quantiles, one for each integer
-quantiles, one for each integer 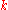 satisfying
satisfying 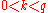 .
.Specialized quantiles
Some q-quantiles have special names:- The 2-quantile is called the medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
- The 3-quantiles are called tertiles or terciles → T
- The 4-quantiles are called quartileQuartileIn descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled...
s → Q - The 5-quantiles are called quintileQuintileQuintile may refer to:*Income quintiles, a division of households by income into five quantiles*Quintiles, a biotechnology research company based in the United States...
s → QU - The 6-quantiles are called sextiles → S
- The 10-quantiles are called decileDecile* In descriptive statistics, any of the nine values that divide the sorted data into ten equal parts, so that each part represents 1/10 of the sample or population* In astrology, an aspect of 36 degrees-See also:*Percentile*Quantile*Quartile*Summary statistics...
s → D - The 12-quantiles are called duo-deciles → Dd
- The 20-quantiles are called vigintiles → V
- The 100-quantiles are called percentilePercentileIn statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
s → P - The 1000-quantiles are called permillePermilleA per mil or per mille is a tenth of a percent or one part per thousand. It is written with the sign ‰ , which looks like a percent sign with an extra zero at the end...
s → Pr
More generally, one can consider the quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
for any distribution. This is defined for real variables between zero and one and is mathematically the inverse of the cumulative distribution function.
Quantiles of a population
For a population of discrete values or for a continuous population density, the th
th 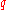 -quantile is the data value where the cumulative distribution function crosses
-quantile is the data value where the cumulative distribution function crosses 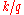 . That
. That  is a
is a 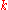 th
th  -quantile for a variable
-quantile for a variable  if
if
-
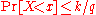 (or, equivalently,
(or, equivalently, 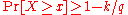 )
)
and
-
 (or, equivalently,
(or, equivalently, 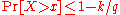 ).
).
For a finite population of
 values indexed 1,...,
values indexed 1,..., from lowest to highest, the
from lowest to highest, the 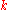 th
th 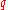 -quantile of this population can be computed via the value of
-quantile of this population can be computed via the value of 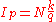 . If
. If 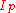 is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the
is not an integer, then round up to the next integer to get the appropriate index; the corresponding data value is the 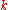 th
th 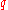 -quantile. On the other hand, if
-quantile. On the other hand, if 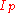 is an integer then any number from the data value at that index to the data value of the next can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating the quantiles).
is an integer then any number from the data value at that index to the data value of the next can be taken as the quantile, and it is conventional (though arbitrary) to take the average of those two values (see Estimating the quantiles).If, instead of using integers
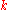 and
and  , the “
, the “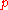 -quantile” is based on a real number
-quantile” is based on a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
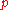 with
with 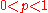 , then
, then  replaces
replaces 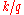 in the above formulae. Some software programs (including Microsoft Excel
in the above formulae. Some software programs (including Microsoft ExcelMicrosoft Excel
Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
) regard the minimum and maximum as the 0th and 100th percentile, respectively; however, such terminology is an extension beyond traditional statistics definitions.
Even-sized population
Consider an ordered population of 10 data values {3, 6, 7, 8, 8, 10, 13, 15, 16, 20}.- The rank of the first quartile is 10×(1/4) = 2.5, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7.
- The rank of the second quartile (same as the median) is 10×(2/4) = 5, which is an integer, while the number of values (10) is an even number, so the average of both the fifth and sixth values is taken—that is (8+10)/2 = 9, though any value from 8 through to 10 could be taken to be the median.
- The rank of the third quartile is 10×(3/4) = 7.5, which rounds up to 8. The eighth value in the population is 15.
Odd-sized population
Consider an ordered population of 11 data values {3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20}.- The first quartile is determined by 11×(1/4) = 2.75, which rounds up to 3, meaning that 3 is the rank in the population (from least to greatest values) at which approximately 1/4 of the values are less than the value of the first quartile. The third value in the population is 7.
- The second quartile value (same as the median) is determined by 11×(2/4) = 5.5, which rounds up to 6. Therefore 6 is the rank in the population (from least to greatest values) at which approximately 2/4 of the values are less than the value of the second quartile (or median). The sixth value in the population is 9.
- The third quartile value for the original example above is determined by 11×(3/4) = 8.25, which rounds up to 9. The ninth value in the population is 15.
Discussion
Standardized test results are commonly misinterpreted as a student scoring "in the 80th percentile," for example, as if the 80th percentile is an interval to score "in," which it is not; one can score "at" some percentile, or between two percentiles, but not "in" some percentile. Perhaps by this example it is meant that the student scores between the 80th and 81st percentiles.If a distribution is symmetric, then the median is the mean (so long as the latter exists). But, in general, the median and the mean differ. For instance, with a random variable that has an exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, any particular sample of this random variable will have roughly a 63% chance of being less than the mean. This is because the exponential distribution has a long tail for positive values but is zero for negative numbers.
Quantiles are useful measures because they are less susceptible to long-tailed distributions and outliers. Empirically, if the data being analyzed are not actually distributed according to an assumed distribution, or if there are other potential sources for outliers that are far removed from the mean, then quantiles may be more useful descriptive statistics than means and other moment-related statistics.
Closely related is the subject of least absolute deviations
Least absolute deviations
Least absolute deviations , also known as Least Absolute Errors , Least Absolute Value , or the L1 norm problem, is a mathematical optimization technique similar to the popular least squares technique that attempts to find a function which closely approximates a set of data...
, a method of regression that is more robust to outliers than is least squares, in which the sum of the absolute value of the observed errors is used in place of the squared error. The connection is that the mean is the single estimate of a distribution that minimizes expected squared error while the median minimizes expected absolute error. Least absolute deviations
Least absolute deviations
Least absolute deviations , also known as Least Absolute Errors , Least Absolute Value , or the L1 norm problem, is a mathematical optimization technique similar to the popular least squares technique that attempts to find a function which closely approximates a set of data...
shares the ability to be relatively insensitive to large deviations in outlying observations, although even better methods of robust regression
Robust regression
In robust statistics, robust regression is a form of regression analysis designed to circumvent some limitations of traditional parametric and non-parametric methods. Regression analysis seeks to find the effect of one or more independent variables upon a dependent variable...
are available.
The quantiles of a random variable are preserved under increasing transformations, in the sense that, for example, if
 is the median of a random variable
is the median of a random variable  , then
, then  is the median of
is the median of 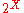 , unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, below, for examples of such interpolation.) Quantiles can also be used in cases where only ordinal
, unless an arbitrary choice has been made from a range of values to specify a particular quantile. (See quantile estimation, below, for examples of such interpolation.) Quantiles can also be used in cases where only ordinalOrdinal
Ordinal may refer to:* Ordinal number , a word representing the rank of a number* Ordinal scale, ranking things that are not necessarily numbers* Ordinal indicator, the sign adjacent to a numeral denoting that it is an ordinal number...
data are available.
Estimating the quantiles of a population
There are several methods for estimatingEstimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
the quantiles. The most comprehensive breadth of methods is available in the R programming language
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, which includes nine sample quantile methods. SAS includes five sample quantile methods, STATA
Stata
Stata is a general-purpose statistical software package created in 1985 by StataCorp. It is used by many businesses and academic institutions around the world...
includes two, and Microsoft Excel
Microsoft Excel
Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
includes one.
In effect, the methods compute Qp, the estimate for the kth q-quantile, where p = k / q, from a sample of size N by computing a real valued index h. When h is an integer, the hth smallest of the N values, xh, is the quantile estimate. Otherwise a rounding or interpolation scheme is used to compute the quantile estimate from h, x⌊h⌋, and x⌈h⌉. (For notation, see floor and ceiling functions).
Estimate types include:
| Type | h | Qp | Notes |
|---|---|---|---|
| R-1, SAS-3 |  |
 |
Inverse of empirical distribution function. When p = 0, use x1. |
| R-2, SAS-5 |  |
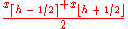 |
The same as R-1, but with averaging at discontinuities. When p = 0, x1. When p = 1, use xN. |
| R-3, SAS-2 | 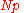 |
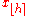 |
The observation numbered closest to Np. Here, ⌊ h ⌉ indicates rounding to the nearest integer, choosing the even integer in the case of a tie. When , use x1. |
| R-4, SAS-1 | 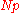 |
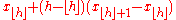 |
Linear interpolation of the empirical distribution function. When , use x1. When p = 1, use xN. |
| R-5 |  |
 |
Piecewise linear function where the knots are the values midway through the steps of the empirical distribution function. When , use x1. When , use xN. |
| R-6, SAS-4 |  |
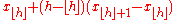 |
Linear interpolation of the expectations for the order statistics for the uniform distribution on [0,1]. When , use x1. When , use xN. |
| R-7, Excel |  |
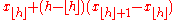 |
Linear interpolation of the modes for the order statistics for the uniform distribution on [0,1]. When p = 1, use xN. |
| R-8 | 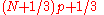 |
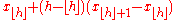 |
Linear interpolation of the approximate medians for order statistics. When , use x1. When , use xN. |
| R-9 | 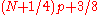 |
 |
The resulting quantile estimates are approximately unbiased for the expected order statistics if x is normally distributed. When , use x1. When , use xN. |
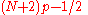 |
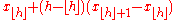 |
If h were rounded, this would give the order statistic with the least expected square deviation relative to p. When , use x1. When , use xN. |
Note that R-3 and R-4 do not give h = (N + 1) / 2 when p = 1/2.
Monte Carlo simulations show that method R-5 is the preferred method for continuous data.
The standard error
Standard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
of a quantile estimate can in general be estimated via the bootstrap. The Maritz-Jarrett method can also be used. Note that a Bayesian approach to quantile estimation (along with a credible interval
Credible interval
In Bayesian statistics, a credible interval is an interval in the domain of a posterior probability distribution used for interval estimation. The generalisation to multivariate problems is the credible region...
) fails with an improper prior and a proper prior is required.
See also
- Summary statisticsSummary statisticsIn descriptive statistics, summary statistics are used to summarize a set of observations, in order to communicate the largest amount as simply as possible...
- Descriptive statisticsDescriptive statisticsDescriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
- QuartileQuartileIn descriptive statistics, the quartiles of a set of values are the three points that divide the data set into four equal groups, each representing a fourth of the population being sampled...
- Q-Q plotQ-Q plotIn statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
- Quantile functionQuantile functionIn probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
- Quantile normalizationQuantile normalizationIn statistics, quantile normalization is a technique for making two distributions identical in statistical properties. To quantile-normalize a test distribution to a reference distribution of the same length, sort the test distribution and sort the reference distribution...
- Quantile regressionQuantile regressionQuantile regression is a type of regression analysis used in statistics. Whereas the method of least squares results in estimates that approximate the conditional mean of the response variable given certain values of the predictor variables, quantile regression results in estimates approximating...

