Noether inequality
Encyclopedia
In mathematics, the Noether inequality, named after Max Noether
, is a property of compact
minimal complex surfaces that restricts the topological type of the underlying topological 4-manifold
. It holds more generally for minimal projective surfaces of general type over an algebraically closed field.
projective surface of general type
defined over an algebraically closed field
(or a smooth minimal compact complex surface of general type) with canonical divisor K = −c1(X), and let pg = h0(K) be the dimension of the space of holomorphic two forms, then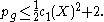
For complex surfaces, an alternative formulation expresses this inequality in terms of topological invariants of the underlying real oriented four manifold. Since a surface of general type is a Kähler surface, the dimension of the maximal positive subspace in intersection form on the second cohomology is given by b+ = 1 + 2pg. Moreover by the Hirzebruch signature theorem c12 (X) = 2e + 3σ, where e = c2(X) is the topological Euler characteristic
and σ = b+ − b− is the signature of the intersection form
. Therefore the Noether inequality can also be expressed as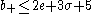
or equivalently using e = 2 – 2 b1 + b+ + b-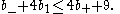
Combining the Noether inequality with the Noether formula 12χ=c12+c2 gives
where q is the irregularity of a surface
, which leads to
a slightly weaker inequality, which is also often called the Noether inequality: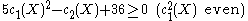
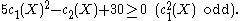
Surfaces where equality holds (i.e. on the Noether line) are called Horikawa surfaces.
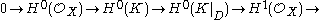
so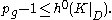
Assume that D is smooth. By the adjunction formula D has a canonical linebundle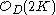
, therefore 
is a special divisor
and the Clifford inequality applies, which gives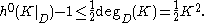
In general, essentially the same argument applies using a more general version of the Clifford inequality for local complete intersections with a dualising line bundle and 1 dimensional sections in the trivial line bundle. These conditions are satisfied for the curve D by the adjunction formula and the fact that D is numerically connected.
Max Noether
Max Noether was a German mathematician who worked on algebraic geometry and the theory of algebraic functions. He has been called "one of the finest mathematicians of the nineteenth century".-Biography:...
, is a property of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
minimal complex surfaces that restricts the topological type of the underlying topological 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
. It holds more generally for minimal projective surfaces of general type over an algebraically closed field.
Formulation of the inequality
Let X be a smooth minimalMinimal model (birational geometry)
In algebraic geometry, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible...
projective surface of general type
Surface of general type
In algebraic geometry, a surface of general type is an algebraic surface with Kodaira dimension 2. Because of Chow's theorem any compact complex manifold of dimension 2 and with Kodaira dimension 2 will actually be an algebraic surface, and in some sense most surfaces are in this...
defined over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
(or a smooth minimal compact complex surface of general type) with canonical divisor K = −c1(X), and let pg = h0(K) be the dimension of the space of holomorphic two forms, then
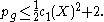
For complex surfaces, an alternative formulation expresses this inequality in terms of topological invariants of the underlying real oriented four manifold. Since a surface of general type is a Kähler surface, the dimension of the maximal positive subspace in intersection form on the second cohomology is given by b+ = 1 + 2pg. Moreover by the Hirzebruch signature theorem c12 (X) = 2e + 3σ, where e = c2(X) is the topological Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
and σ = b+ − b− is the signature of the intersection form
Intersection form
Intersection form may refer to:*Intersection theory *intersection form...
. Therefore the Noether inequality can also be expressed as
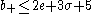
or equivalently using e = 2 – 2 b1 + b+ + b-
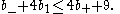
Combining the Noether inequality with the Noether formula 12χ=c12+c2 gives
where q is the irregularity of a surface
Irregularity of a surface
In mathematics, the irregularity of a complex surface X is the Hodge number h0,1= dim H1, usually denoted by q . The irregularity of an algebraic surface is sometimes defined to be this Hodge number, and sometimes defined to be the dimension of the Picard variety , which is the same in...
, which leads to
a slightly weaker inequality, which is also often called the Noether inequality:
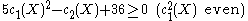
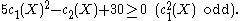
Surfaces where equality holds (i.e. on the Noether line) are called Horikawa surfaces.
Proof sketch
It follows from the minimal general type condition that K2 > 0. We may thus assume that pg > 1, since the inequality is otherwise automatic. In particular, we may assume there is an effective divisor D representing K. We then have an exact sequence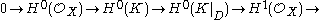so
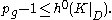
Assume that D is smooth. By the adjunction formula D has a canonical linebundle
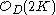, therefore is a special divisorSpecial divisor
In mathematics, in the theory of algebraic curves, certain divisors on a curve C are particular, in the sense of determining more compatible functions than would be predicted. These are the special divisors...
and the Clifford inequality applies, which gives
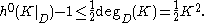
In general, essentially the same argument applies using a more general version of the Clifford inequality for local complete intersections with a dualising line bundle and 1 dimensional sections in the trivial line bundle. These conditions are satisfied for the curve D by the adjunction formula and the fact that D is numerically connected.