Minimal model (birational geometry)
Encyclopedia
In algebraic geometry
, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible. The subject has its origins in the classical birational geometry of surfaces studied by the Italian school
, and is currently an active research area within algebraic geometry.
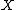for which any birational morphism
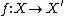is an isomorphism
.
In the modern formulation, the goal of the theory is as follows. Suppose we are given a projective variety
, which for simplicity is assumed nonsingular. There are two cases:
The question of nonsingularity of the varieties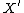
and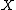 
appearing above is an important one. It seems natural to hope that if we start with smooth 
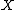, then we can always find a minimal model or Fano fibre space inside the category of smooth varieties. However, this is not true, and so it becomes necessary to consider singular varieties also. The singularities that appear are called terminal singularities.
essentially describes the process of constructing a minimal model of any smooth surface. The theorem states that any nontrivial birational morphism f:X→Y must contract a −1-curve to a smooth point, and conversely any such curve can be smoothly contracted. Here a −1-curve is a smooth rational curve C with self-intersection C.C = −1. Any such curve must have K.C=−1 which shows that if the canonical class is nef then the surface has no −1-curves.
Castelnuovo's theorem implies that to construct a minimal model for a smooth surface, we simply contract all the −1-curves on the surface, and the resulting variety Y is either a (unique) minimal model with K nef, or a ruled surface (which is the same as a 2-dimensional Fano fiber space, and is either a projective plane or a ruled surface over a curve). In the second case, the ruled surface birational to X is not unique, though there is a unique one isomorphic to the product of the projective line and a curve.
which are not birational to any smooth variety 
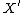with nef canonical class. The major conceptual advance of the 1970s and early 1980s was that the construction of minimal models is still feasible, provided one is careful about the types of singularities which occur. (For example, we want to decide if 
is nef, so intersection numbers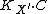 
must be defined. Hence, at the very least, our varieties must have 
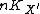Cartier for some positive integer 
.)
The first key result is the Cone theorem
of Mori
, describing the structure of the cone of curves of
. Briefly, the theorem shows that starting with 
, one can inductively construct a sequence of varieties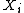 
, each of which is 'closer' than the previous one to having 
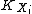nef. However, the process may encounter difficulties: at some point the variety 
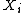may become 'too singular'. The conjectural solution to this problem is the flip
, a kind of codimension-2 surgery operation on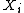
. It is not clear that the required flips exist, nor that they always terminate (that is, that one reaches a minimal model 
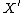in finitely many steps.) showed that flips exist in the 3-dimensional case; much recent work has focused on existence and termination problems in higher dimensions.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible. The subject has its origins in the classical birational geometry of surfaces studied by the Italian school
Italian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
, and is currently an active research area within algebraic geometry.
Outline
The basic idea of the theory is to simplify the birational classification of varieties by finding, in each birational equivalence class, a variety which is "as simple as possible". The precise meaning of this phrase has evolved with the development of the subject; originally for surfaces, it meant finding a smooth variety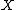 for which any birational morphismRegular map
Regular map may refer to:* a regular map , in algebraic geometry, an everywhere-defined, polynomial function of algebraic varieties.* a regular map , a symmetric 2-cell embedding of a graph into a closed surface....
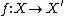is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
In the modern formulation, the goal of the theory is as follows. Suppose we are given a projective variety
, which for simplicity is assumed nonsingular. There are two cases:
- If
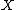has Kodaira dimensionKodaira dimensionIn algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
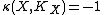, we want to find a variety 
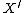birational to 
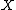, and a morphism 
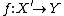to a projective variety 
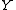such that 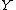dim 
< dim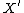
, with the anticanonical class 
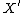of a general fibre 
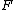being ampleAmple line bundleIn algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
. Such a morphism is called a Fano fibre space. - If
is at least 0, we want to find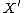 
birational to 
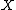, with the canonical class 
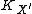nefNumerically effectiveA line bundle on an algebraic variety is said to be nef , if the degree of the restriction to any algebraic curve of the variety is non-negative.In particular, every ample line bundle is nef....
. In this case,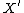
is a minimal model for 
.
The question of nonsingularity of the varieties
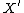and 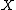appearing above is an important one. It seems natural to hope that if we start with smooth 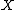, then we can always find a minimal model or Fano fibre space inside the category of smooth varieties. However, this is not true, and so it becomes necessary to consider singular varieties also. The singularities that appear are called terminal singularities.Minimal models of surfaces
Every irreducible complex algebraic curve is birational to a unique smooth projective curve, so the theory for curves is trivial. The case of surfaces was first investigated by the geometers of the Italian school around 1900; the contraction theorem of CastelnuovoGuido Castelnuovo
Guido Castelnuovo was an Italian mathematician. His father, Enrico Castelnuovo, was a novelist and campaigner for the unification of Italy...
essentially describes the process of constructing a minimal model of any smooth surface. The theorem states that any nontrivial birational morphism f:X→Y must contract a −1-curve to a smooth point, and conversely any such curve can be smoothly contracted. Here a −1-curve is a smooth rational curve C with self-intersection C.C = −1. Any such curve must have K.C=−1 which shows that if the canonical class is nef then the surface has no −1-curves.
Castelnuovo's theorem implies that to construct a minimal model for a smooth surface, we simply contract all the −1-curves on the surface, and the resulting variety Y is either a (unique) minimal model with K nef, or a ruled surface (which is the same as a 2-dimensional Fano fiber space, and is either a projective plane or a ruled surface over a curve). In the second case, the ruled surface birational to X is not unique, though there is a unique one isomorphic to the product of the projective line and a curve.
Higher-dimensional minimal models
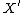In dimensions greater than 2, the theory becomes far more involved. In particular, there exist smooth varieties which are not birational to any smooth variety with nef canonical class. The major conceptual advance of the 1970s and early 1980s was that the construction of minimal models is still feasible, provided one is careful about the types of singularities which occur. (For example, we want to decide if is nef, so intersection numbers 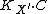must be defined. Hence, at the very least, our varieties must have 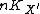Cartier for some positive integer .)The first key result is the Cone theorem
Cone of curves
In mathematics, the cone of curves of an algebraic variety X is a combinatorial invariant of much importance to the birational geometry of X.-Definition:Let X be a proper variety...
of Mori
Shigefumi Mori
-References:*Heisuke Hironaka, Fields Medallists Lectures, Michael F. Atiyah , Daniel Iagolnitzer ; World Scientific Publishing, 2007. ISBN 9810231172...
, describing the structure of the cone of curves of
. Briefly, the theorem shows that starting with , one can inductively construct a sequence of varieties 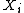, each of which is 'closer' than the previous one to having 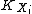nef. However, the process may encounter difficulties: at some point the variety 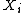may become 'too singular'. The conjectural solution to this problem is the flipFlip (algebraic geometry)
In algebraic geometry, flips and flops are codimension-2 surgery operations arising in the minimal model program, given by blowing up along a relative canonical ring. In dimension 3 flips are used to construct minimal models, and any two birationally equivalent minimal models are connected by...
, a kind of codimension-2 surgery operation on
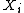. It is not clear that the required flips exist, nor that they always terminate (that is, that one reaches a minimal model 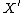in finitely many steps.) showed that flips exist in the 3-dimensional case; much recent work has focused on existence and termination problems in higher dimensions.