
Nakamura number
Encyclopedia
In cooperative game theory
and social choice theory
, the Nakamura number measures the degree of rationality
of preference aggregation rules (collective decision rules), such as voting rules.
It is an indicator of the extent to which an aggregation rule can yield well-defined choices.
In contrast,
The larger the Nakamura number a rule has, the greater the number of alternatives the rule can rationally deal with.
For example, since (except in the case of four individuals (voters)) the Nakamura number of majority rule is three,
the rule can deal with up to two alternatives rationally (without causing a paradox).
The number is named after Kenjiro Nakamura (1947–1979), a Japanese game theorist who proved the above fact
that the rationality of collective choice critically depends on the number of alternatives.
to which a Nakamura number will be assigned.
Suppose the set of individuals consists of individuals 1, 2, 3, 4, and 5.
Behind majority rule is the following collection of ("decisive") coalitions (subsets of individuals) having at least three members:
A Nakamura number can be assigned to such collections, which we call simple games.
More precisely, a simple game is just an arbitrary collection of coalitions;
the coalitions belonging to the collection are said to be winning; the others losing.
If all the (at least three, in the example above) members of a winning coalition prefer alternative x to alternative y,
then the society (of five individuals, in the example above) will adopt the same ranking (social preference).
The Nakamura number of a simple game is defined as the minimum number of winning coalitions with empty intersection
.
(By intersecting this number of winning coalitions, one can sometimes obtain an empty set.
But by intersecting less than this number, one can never obtain an empty set.)
The Nakamura number of the simple game above is three, for example,
since the intersection of any two winning coalitions contains at least one individual
but the intersection of the following three winning coalitions is empty: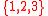 ,
, 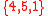 ,
, 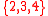 .
.
Nakamura's theorem (1979) gives the following necessary (also sufficient if the set of alternatives is finite) condition for a simple game to have a nonempty "core" (the set of socially "best" alternatives) for all profiles of individual preferences:
the number of alternatives is less than the Nakamura number of the simple game.
Here, the core of a simple game with respect to the profile of preferences is the set of all alternatives
such that there is no alternative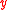
that every individual in a winning coalition prefers to ; that is, the set of maximal elements of the social preference.
; that is, the set of maximal elements of the social preference.
For the majority game example above, the theorem implies that the core will be empty (no alternative will be deemed "best") for some profile,
if there are three or more alternatives.
Variants of Nakamura's theorem exist that provide a condition for the core to be nonempty
(i) for all profiles of acyclic preferences;
(ii) for all profiles of transitive preferences; and
(iii) for all profiles of linear orders.
There is a different kind of variant (Kumabe and Mihara, 2011),
which dispenses with acyclicity, the weak requirement of rationality.
The variant gives a condition for the core to be nonempty for all profiles of preferences that have maximal elements.
For ranking alternatives, there is a very well known result called "Arrow's impossibility theorem
" in social choice theory,
which points out the difficulty for a group of individuals in ranking three or more alternatives.
For choosing from a set of alternatives (instead of ranking them), Nakamura's theorem is more relevant.
An interesting question is how large the Nakamura number can be.
It has been shown that for a (finite or) algorithmically computable simple game that has no veto player
(an individual that belongs to every winning coalition)
to have a Nakamura number greater than three, the game has to be non-strong.
This means that there is a losing (i.e., not winning) coalition whose complement is also losing.
This in turn implies that nonemptyness of the core is assured for a set of three or more alternatives
only if the core may contain several alternatives that cannot be strictly ranked.
 be a (finite or infinite) nonempty set of individuals.
be a (finite or infinite) nonempty set of individuals.
The subsets of are called coalitions.
are called coalitions.
A simple game (voting game) is a collection of coalitions.
of coalitions.
(Equivalently, it is a coalitional game that assigns either 1 or 0 to each coalition.)
We assume that is nonempty and does not contain an empty set.
is nonempty and does not contain an empty set.
The coalitions belonging to are winning; the others are losing.
are winning; the others are losing.
A simple game is monotonic if
is monotonic if  and
and 
imply .
.
It is proper if implies
implies  .
.
It is strong if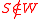 imples
imples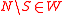 .
.
A veto player (vetoer) is an individual that belongs to all winning coalitions.
A simple game is nonweak if it has no veto player.
It is finite if there is a finite set (called a carrier) such that for all coalitions
such that for all coalitions 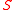 ,
,
we have iff
iff 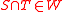 .
.
Let be a (finite or infinite) set of alternatives, whose cardinal number
be a (finite or infinite) set of alternatives, whose cardinal number
(the number of elements)
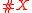 is at least two.
is at least two.
A (strict) preference is an asymmetric relation on
on  :
:
if (read "
(read " is preferred to
is preferred to  "),
"),
then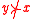 .
.
We say that a preference is acyclic (does not contain cycles) if
is acyclic (does not contain cycles) if
for any finite number of alternatives ,
,
whenever ,
,  ,…,
,…, 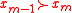 ,
,
we have . Note that acyclic relations are asymmetric, hence preferences.
. Note that acyclic relations are asymmetric, hence preferences.
A profile is a list of individual preferences
of individual preferences 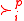 .
.
Here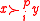 means that individual
means that individual  prefers alternative
prefers alternative 
to at profile
at profile 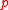 .
.
A simple game with ordinal preferences is a pair consisting
consisting
of a simple game and a profile
and a profile 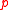 .
.
Given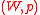 , a dominance (social preference) relation
, a dominance (social preference) relation 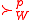 is defined
is defined
on by
by  if and only if there is a winning coalition
if and only if there is a winning coalition 
satisfying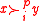 for all
for all 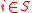 .
.
The core of
of 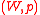 is the set of alternatives undominated by
is the set of alternatives undominated by 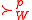
(the set of maximal elements of with respect to
with respect to 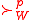 ):
): if and only if there is no
if and only if there is no 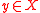 such that
such that 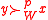 .
.
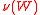 of a simple game
of a simple game  is the size (cardinal number)
is the size (cardinal number)
of the smallest collection of winning coalitions with empty intersection: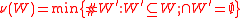
if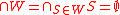 (no veto player);
(no veto player);
otherwise, (greater than any cardinal number).
(greater than any cardinal number).
it is easy to prove that if is a simple game without a veto player, then
is a simple game without a veto player, then 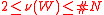 .
.
Examples for finitely many individuals (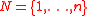 ) (see Austen-Smith and Banks (1999), Lemma 3.2).
) (see Austen-Smith and Banks (1999), Lemma 3.2).
Let be a simple game that is monotonic and proper.
be a simple game that is monotonic and proper.
Examples for at most countably many individuals (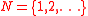 ).
).
Kumabe and Mihara (2008) comprehensively study the restrictions that various properties
(monotonicity, properness, strongness, nonweakness, and finiteness) for simple games
impose on their Nakamura number (the Table "Possible Nakamura Numbers" below summarizes the results).
In particular, they show that an algorithmically computable simple
game
without a veto player has a Nakamura number greater than 3 only if it is proper and nonstrong.
Let be a simple game. Then the core
be a simple game. Then the core  is nonempty for all profiles
is nonempty for all profiles 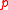 of acyclic preferences if and only if
of acyclic preferences if and only if  is finite and
is finite and 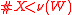 .
.
Remarks
Cooperative game
In game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
and social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
, the Nakamura number measures the degree of rationality
of preference aggregation rules (collective decision rules), such as voting rules.
It is an indicator of the extent to which an aggregation rule can yield well-defined choices.
- If the number of alternatives (candidates; options) to choose from is less than this number, then the rule in question will identify "best" alternatives without any problem.
In contrast,
- if the number of alternatives is greater than or equal to this number, the rule will fail to identify "best" alternatives for some pattern of voting (i.e., for some profile (tupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
) of individual preferences), because a voting paradoxVoting paradoxThe voting paradox is a situation noted by the Marquis de Condorcet in the late 18th century, in which collective preferences can be cyclic , even if the preferences of individual voters are not. This is paradoxical, because it means that majority wishes can be in conflict with each other...
will arise (a cycle generated such as alternative socially preferred to alternative
socially preferred to alternative 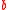 ,
, 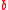 to
to  , and
, and  to
to  ).
).
The larger the Nakamura number a rule has, the greater the number of alternatives the rule can rationally deal with.
For example, since (except in the case of four individuals (voters)) the Nakamura number of majority rule is three,
the rule can deal with up to two alternatives rationally (without causing a paradox).
The number is named after Kenjiro Nakamura (1947–1979), a Japanese game theorist who proved the above fact
that the rationality of collective choice critically depends on the number of alternatives.
Overview
To introduce a precise definition of the Nakamura number, we give an example of a "game" (underlying the rule in question)to which a Nakamura number will be assigned.
Suppose the set of individuals consists of individuals 1, 2, 3, 4, and 5.
Behind majority rule is the following collection of ("decisive") coalitions (subsets of individuals) having at least three members:
- { {1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5} }
A Nakamura number can be assigned to such collections, which we call simple games.
More precisely, a simple game is just an arbitrary collection of coalitions;
the coalitions belonging to the collection are said to be winning; the others losing.
If all the (at least three, in the example above) members of a winning coalition prefer alternative x to alternative y,
then the society (of five individuals, in the example above) will adopt the same ranking (social preference).
The Nakamura number of a simple game is defined as the minimum number of winning coalitions with empty intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
(By intersecting this number of winning coalitions, one can sometimes obtain an empty set.
But by intersecting less than this number, one can never obtain an empty set.)
The Nakamura number of the simple game above is three, for example,
since the intersection of any two winning coalitions contains at least one individual
but the intersection of the following three winning coalitions is empty:
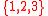 ,
, 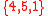 ,
, 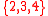 .
.Nakamura's theorem (1979) gives the following necessary (also sufficient if the set of alternatives is finite) condition for a simple game to have a nonempty "core" (the set of socially "best" alternatives) for all profiles of individual preferences:
the number of alternatives is less than the Nakamura number of the simple game.
Here, the core of a simple game with respect to the profile of preferences is the set of all alternatives

such that there is no alternative
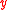
that every individual in a winning coalition prefers to
 ; that is, the set of maximal elements of the social preference.
; that is, the set of maximal elements of the social preference.For the majority game example above, the theorem implies that the core will be empty (no alternative will be deemed "best") for some profile,
if there are three or more alternatives.
Variants of Nakamura's theorem exist that provide a condition for the core to be nonempty
(i) for all profiles of acyclic preferences;
(ii) for all profiles of transitive preferences; and
(iii) for all profiles of linear orders.
There is a different kind of variant (Kumabe and Mihara, 2011),
which dispenses with acyclicity, the weak requirement of rationality.
The variant gives a condition for the core to be nonempty for all profiles of preferences that have maximal elements.
For ranking alternatives, there is a very well known result called "Arrow's impossibility theorem
Arrow's impossibility theorem
In social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
" in social choice theory,
which points out the difficulty for a group of individuals in ranking three or more alternatives.
For choosing from a set of alternatives (instead of ranking them), Nakamura's theorem is more relevant.
An interesting question is how large the Nakamura number can be.
It has been shown that for a (finite or) algorithmically computable simple game that has no veto player
(an individual that belongs to every winning coalition)
to have a Nakamura number greater than three, the game has to be non-strong.
This means that there is a losing (i.e., not winning) coalition whose complement is also losing.
This in turn implies that nonemptyness of the core is assured for a set of three or more alternatives
only if the core may contain several alternatives that cannot be strictly ranked.
Framework
Let be a (finite or infinite) nonempty set of individuals.
be a (finite or infinite) nonempty set of individuals.The subsets of
 are called coalitions.
are called coalitions.A simple game (voting game) is a collection
 of coalitions.
of coalitions.(Equivalently, it is a coalitional game that assigns either 1 or 0 to each coalition.)
We assume that
 is nonempty and does not contain an empty set.
is nonempty and does not contain an empty set.The coalitions belonging to
 are winning; the others are losing.
are winning; the others are losing.A simple game
 is monotonic if
is monotonic if  and
and 
imply
 .
.It is proper if
 implies
implies  .
.It is strong if
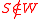 imples
imples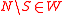 .
.A veto player (vetoer) is an individual that belongs to all winning coalitions.
A simple game is nonweak if it has no veto player.
It is finite if there is a finite set (called a carrier)
 such that for all coalitions
such that for all coalitions 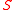 ,
,we have
 iff
iff 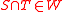 .
.Let
 be a (finite or infinite) set of alternatives, whose cardinal number
be a (finite or infinite) set of alternatives, whose cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
(the number of elements)
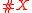 is at least two.
is at least two.A (strict) preference is an asymmetric relation
 on
on  :
:if
 (read "
(read " is preferred to
is preferred to  "),
"),then
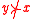 .
.We say that a preference
 is acyclic (does not contain cycles) if
is acyclic (does not contain cycles) iffor any finite number of alternatives
 ,
,whenever
 ,
,  ,…,
,…, 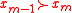 ,
,we have
 . Note that acyclic relations are asymmetric, hence preferences.
. Note that acyclic relations are asymmetric, hence preferences.A profile is a list
 of individual preferences
of individual preferences 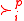 .
.Here
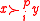 means that individual
means that individual  prefers alternative
prefers alternative 
to
 at profile
at profile 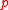 .
.A simple game with ordinal preferences is a pair
 consisting
consistingof a simple game
 and a profile
and a profile 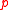 .
.Given
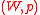 , a dominance (social preference) relation
, a dominance (social preference) relation 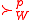 is defined
is definedon
 by
by  if and only if there is a winning coalition
if and only if there is a winning coalition 
satisfying
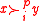 for all
for all 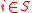 .
.The core
 of
of 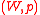 is the set of alternatives undominated by
is the set of alternatives undominated by 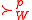
(the set of maximal elements of
 with respect to
with respect to 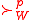 ):
): if and only if there is no
if and only if there is no 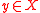 such that
such that 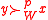 .
.The Nakamura number: the definition and examples
The Nakamura number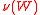 of a simple game
of a simple game  is the size (cardinal number)
is the size (cardinal number)of the smallest collection of winning coalitions with empty intersection:
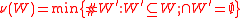
if
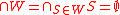 (no veto player);
(no veto player);otherwise,
 (greater than any cardinal number).
(greater than any cardinal number).it is easy to prove that if
 is a simple game without a veto player, then
is a simple game without a veto player, then 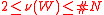 .
.Examples for finitely many individuals (
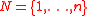 ) (see Austen-Smith and Banks (1999), Lemma 3.2).
) (see Austen-Smith and Banks (1999), Lemma 3.2).Let
 be a simple game that is monotonic and proper.
be a simple game that is monotonic and proper.
- If
 is strong and without a veto player, then
is strong and without a veto player, then 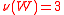 .
. - If
 is the majority game (i.e., a coalition is wining if and only if it consists of more than half of individuals), then
is the majority game (i.e., a coalition is wining if and only if it consists of more than half of individuals), then 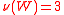 if
if 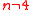 ;
; 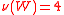 if
if  .
. - If
 is a
is a 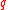 -rule (i.e., a coalition is winning if and only if it consists of at least
-rule (i.e., a coalition is winning if and only if it consists of at least 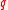 individuals) with
individuals) with 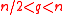 , then
, then 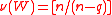 , where
, where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to  .
.
Examples for at most countably many individuals (
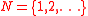 ).
).Kumabe and Mihara (2008) comprehensively study the restrictions that various properties
(monotonicity, properness, strongness, nonweakness, and finiteness) for simple games
impose on their Nakamura number (the Table "Possible Nakamura Numbers" below summarizes the results).
In particular, they show that an algorithmically computable simple
game
without a veto player has a Nakamura number greater than 3 only if it is proper and nonstrong.
| Type | Finite games | Infinite games |
|---|---|---|
| 1111 | 3 | 3 |
| 1110 | +∞ | none |
| 1101 | ≥3 | ≥3 |
| 1100 | +∞ | +∞ |
| 1011 | 2 | 2 |
| 1010 | none | none |
| 1001 | 2 | 2 |
| 1000 | none | none |
| 0111 | 2 | 2 |
| 0110 | none | none |
| 0101 | ≥2 | ≥2 |
| 0100 | +∞ | +∞ |
| 0011 | 2 | 2 |
| 0010 | none | none |
| 0001 | 2 | 2 |
| 0000 | none | none |
Nakamura's theorem for acyclic preferences
Nakamura's theorem (Nakamura, 1979, Theorems 2.3 and 2.5).Let
 be a simple game. Then the core
be a simple game. Then the core  is nonempty for all profiles
is nonempty for all profiles 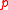 of acyclic preferences if and only if
of acyclic preferences if and only if  is finite and
is finite and 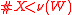 .
.Remarks
- Nakamura's theorem is often cited in the following form, without reference to the core (e.g., Austen-Smith and Banks, 1999, Theorem 3.2): The dominance relation
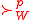 is acyclic for all profiles
is acyclic for all profiles 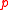 of acyclic preferences if and only if
of acyclic preferences if and only if 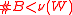 for all finite
for all finite  (Nakamura 1979, Theorem 3.1).
(Nakamura 1979, Theorem 3.1).
- The statement of the theorem remains valid if we replace "for all profiles
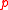 of acyclic preferences" by "for all profiles
of acyclic preferences" by "for all profiles 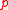 of negatively transitive preferences" or by "for all profiles
of negatively transitive preferences" or by "for all profiles 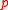 of linearly ordered (i.e., transitive and total) preferences".
of linearly ordered (i.e., transitive and total) preferences".
- The theorem can be extended to
 -simple games. Here, the collection
-simple games. Here, the collection  of coalitions is an arbitrary Boolean algebra of subsets of
of coalitions is an arbitrary Boolean algebra of subsets of  , such as the
, such as the  -algebra of Lebesgue measurableLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
-algebra of Lebesgue measurableLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
sets. A -simple game is a subcollection of
-simple game is a subcollection of  . Profiles are suitably restricted to measurable ones: a profile
. Profiles are suitably restricted to measurable ones: a profile 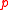 is measurable if for all
is measurable if for all 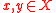 , we have
, we have 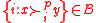 .
.
A variant of Nakamura's theorem for preferences that may contain cycles
In this section, we discard the usual assumption of acyclic preferences.
Instead, we restrict preferences to those having a maximal element on a given agenda (opportunity set that a group of individuals are confronted with),
a subset of some underlying set of alternatives.
(This weak restriction on preferences might be of some interest from the viewpoint of behavioral economics.)
Accordingly, it is appropriate to think of as an agenda here.
as an agenda here.
An alternative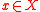 is a maximal element with respect to
is a maximal element with respect to 
(i.e.,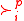 has a maximal element
has a maximal element  ) if there is no
) if there is no 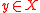 such that
such that 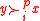 . If a preference is acyclic over the underlying set of alternatives, then it has a maximal element on every finite subset
. If a preference is acyclic over the underlying set of alternatives, then it has a maximal element on every finite subset  .
.
We introduce a strengthening of the core before stating the variant of Nakamura's theorem.
An alternative can be in the core
can be in the core  even if there is a winning coalition of individuals
even if there is a winning coalition of individuals  that are "dissatisfied" with
that are "dissatisfied" with 
(i.e., each prefers some
prefers some 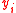 to
to  ).
).
The following solution excludes such an :
:
- An alternative
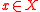 is in the core
is in the core 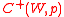 without majority dissatisfaction if there is no winning coalition
without majority dissatisfaction if there is no winning coalition  such that for all
such that for all  ,
,  is non-maximal (there exists some
is non-maximal (there exists some 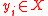 satisfying
satisfying  ).
).
It is easy to prove that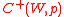 depends only on the set of maximal elements of each individual and is included in the union of such sets.
depends only on the set of maximal elements of each individual and is included in the union of such sets.
Moreover, for each profile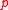 , we have
, we have 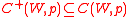 .
.
A variant of Nakamura's theorem (Kumabe and Mihara, Theorem 2).
Let be a simple game. Then the following three statements are equivalent:
be a simple game. Then the following three statements are equivalent:
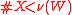 ;
;- the core
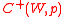 without majority dissatisfaction is nonempty for all profiles
without majority dissatisfaction is nonempty for all profiles 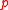 of preferences that have a maximal element;
of preferences that have a maximal element; - the core
 is nonempty for all profiles
is nonempty for all profiles 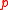 of preferences that have a maximal element.
of preferences that have a maximal element.
Remarks
- Unlike Nakamura's original theorem,
 being finite is not a necessary condition for
being finite is not a necessary condition for 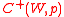 or
or  to be nonempty for all profiles
to be nonempty for all profiles 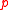 . Even if an agenda
. Even if an agenda  has infinitely many alternatives, there is an element in the cores for appropriate profiles, as long as the inequality
has infinitely many alternatives, there is an element in the cores for appropriate profiles, as long as the inequality 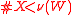 is satisfied.
is satisfied.
- The statement of the theorem remains valid if we replace "for all profiles
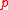 of preferences that have a maximal element" in statements 2 and 3 by "for all profiles
of preferences that have a maximal element" in statements 2 and 3 by "for all profiles 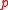 of preferences that have exactly one maximal element" or "for all profiles
of preferences that have exactly one maximal element" or "for all profiles 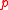 of linearly ordered preferences that have a maximal element" (Kumabe and Mihara, Proposition 1).
of linearly ordered preferences that have a maximal element" (Kumabe and Mihara, Proposition 1).
- Like Nakamura's theorem for acyclic preferences, this theorem can be extended to
 -simple games. The theorem can be extended even further (1 and 2 are equivalent; they imply 3) to collections
-simple games. The theorem can be extended even further (1 and 2 are equivalent; they imply 3) to collections  of winning sets by extending the notion of the Nakamura number.
of winning sets by extending the notion of the Nakamura number.
- The theorem can be extended to

