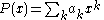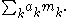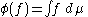Moment problem
Encyclopedia
In mathematics
, a moment problem arises as the result of trying to invert the mapping that takes a measure
μ to the sequences of moment
s
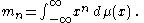
More generally, one may consider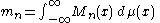
for an arbitrary sequence of functions Mn.
, and M is in the sequence { xn : n = 0, 1, 2, ... } In this form the question appears in probability theory
, asking whether there is a probability measure
having specified mean
, variance
and so on, and whether it is unique.
There are three named classical moment problems: the Hamburger moment problem in which the support
of μ is allowed to be the whole real line; the Stieltjes moment problem, for[0, +∞) ; and the Hausdorff moment problem for a bounded interval, which without loss of generality
may be taken as [0, 1].
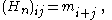
should be positive semi-definite
. A condition of similar form is necessary and sufficient for the existence of a measure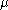
supported on a given interval [a, b].
One way to prove these results is to consider the linear functional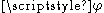
that sends a polynomial
to
If mkn are the moments of some measure μ supported on [a, b], then evidently
Vice versa, if holds, one can apply the M. Riesz extension theorem
and extend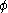
to a functional on the space of continuous functions with compact support C0([a, b]), so that
such that ƒ ≥ 0 on [a, b].
By the Riesz representation theorem, holds iff there exists a measure μ supported on [a, b], such that
for every ƒ ∈ C0([a, b]).
Thus the existence of the measure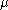
is equivalent to . Using a representation theorem for positive polynomials on [a, b], one can reformulate as a condition on Hankel matrices.
See Refs. 1–3. for more details.
s are dense
under the uniform norm in the space of continuous functions on [0, 1]. For the problem on an infinite interval, uniqueness is a more delicate question; see Carleman's condition
, Krein's condition and Ref. 2.
. See also: Chebyshev–Markov–Stieltjes inequalities and Ref. 3.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a moment problem arises as the result of trying to invert the mapping that takes a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
μ to the sequences of moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s
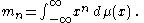
More generally, one may consider
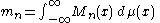
for an arbitrary sequence of functions Mn.
Introduction
In the classical setting, μ is a measure on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, and M is in the sequence { xn : n = 0, 1, 2, ... } In this form the question appears in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, asking whether there is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
having specified mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and so on, and whether it is unique.
There are three named classical moment problems: the Hamburger moment problem in which the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of μ is allowed to be the whole real line; the Stieltjes moment problem, for
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
may be taken as [0, 1].
Existence
A sequence of numbers mn is the sequence of moments of a measure μ if and only if a certain positivity condition is fulfilled; namely, the Hankel matrices Hn,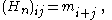should be positive semi-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. A condition of similar form is necessary and sufficient for the existence of a measure
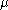supported on a given interval [a, b].One way to prove these results is to consider the linear functional
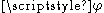that sends a polynomial
to
If mkn are the moments of some measure μ supported on [a, b], then evidently
Vice versa, if holds, one can apply the M. Riesz extension theorem
M. Riesz extension theorem
The M. Riesz extension theorem is a theorem in mathematics, proved by Marcel Riesz during his study of the problem of moments.-Formulation:Let E be a real vector space, F ⊂ E a vector subspace, and let K ⊂ E be a convex cone.A linear functional ...
and extend
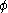to a functional on the space of continuous functions with compact support C0([a, b]), so thatsuch that ƒ ≥ 0 on [a, b].
By the Riesz representation theorem, holds iff there exists a measure μ supported on [a, b], such that
for every ƒ ∈ C0([a, b]).
Thus the existence of the measure
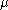is equivalent to . Using a representation theorem for positive polynomials on [a, b], one can reformulate as a condition on Hankel matrices.See Refs. 1–3. for more details.
Uniqueness (or determinacy)
The uniqueness of μ in the Hausdorff moment problem follows from the Weierstrass approximation theorem, which states that polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s are dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
under the uniform norm in the space of continuous functions on [0, 1]. For the problem on an infinite interval, uniqueness is a more delicate question; see Carleman's condition
Carleman's condition
In mathematics, Carleman's condition is a sufficient condition for the determinacy of the moment problem.-Hamburger moment problem:For the Hamburger moment problem, the theorem, proved by Torsten Carleman, states the following:...
, Krein's condition and Ref. 2.
Variations
An important variation is the truncated moment problem, which studies the properties of measures with fixed first k moments (for a finite k). Results on the truncated moment problem have numerous applications to extremal problems, optimisation and limit theorems in probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. See also: Chebyshev–Markov–Stieltjes inequalities and Ref. 3.