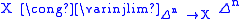Simplicial set
Encyclopedia
In mathematics
, a simplicial set is a construction in categorical
homotopy theory which is a purely algebraic model of the notion of a "well-behaved
" topological space. Historically, this model arose from earlier work in combinatorial topology
and in particular from the notion of simplicial complex
es.
s which can be built up (or faithfully represented up to homotopy) from simplices
and their incidence relations. This is similar to the approach of CW complex
es to modeling topological spaces, with the crucial difference that simplicial sets are purely algebraic and do not carry any actual topology (this will become clear in the formal definition).
To get back to actual topological spaces, there is a geometric realization functor
available which takes values in the category of compactly generated Hausdorff spaces. Most classical results on CW complexes in homotopy theory have analogous versions for simplicial sets which generalize these results. While algebraic topologists largely continue to prefer CW complexes, there is a growing contingent of researchers interested in using simplicial sets for applications in algebraic geometry
where CW complexes do not naturally exist.
, a simplicial set X is a contravariant functor
where Δ denotes the simplex category whose objects are finite strings of ordinal numbers of the form
(or in other words non-empty totally ordered finite sets) and whose morphisms are order-preserving functions between them, and Set is the category of small sets
.
It is common to define simplicial sets as a covariant functor from the opposite category
, as
This definition is clearly equivalent to the one immediately above.
Alternatively, one can think of a simplicial set as a simplicial object (see below) in the category Set, but this is only different language for the definition just given. If we use a covariant functor X instead of a contravariant one, we arrive at the definition of a cosimplicial set.
Simplicial sets form a category usually denoted sSet or just S whose objects are simplicial sets and whose morphisms are natural transformations between them. There is a corresponding category for cosimplicial sets as well, denoted by cSet.
These definitions arise from the relationship of the conditions imposed on the face maps and degeneracy maps to the category Δ.
The face maps
di :
n
→
n − 1
are given by
The degeneracy maps
si :
n
→
n + 1
are given by
By definition, these maps satisfy the following simplicial identities:
The simplicial category Δ has as its morphisms the monotonic non-decreasing functions. Since the morphisms are generated by those that 'skip' or 'add' a single element, the detailed relations written out above underlie the topological applications. It can be shown that these relations suffice.
The geometric realization |Δn| is just defined to be the standard topological n-simplex in general position given by
By the Yoneda lemma
, the n-simplices of a simplicial set X are classified by natural transformations in hom(Δn, X). The n-simplices of X are then collectively denoted by Xn. Furthermore, there is a simplex category, denoted by
whose objects are maps Δn → X and whose morphisms are natural transformations Δn → Δm over X arising from maps n → m in Δ. The following isomorphism shows that a simplicial set X is a colimit of its simplices:
where the colimit is taken over the simplex category of X.
This larger category is used as the target of the functor because, in particular, a product of simplicial sets
is realized as a product
of the corresponding topological spaces, where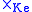
denotes the Kelley space product. To define the realization functor, we first define it on n-simplices Δn as the corresponding topological n-simplex |Δn|. The definition then naturally extends to any simplicial set X by setting
where the colimit is taken over the n-simplex category of X. The geometric realization is functorial on S.
of "probing" a target topological space with standard topological n-simplices. Furthermore, the singular functor S is right adjoint to the geometric realization functor described above, i.e.:
for any simplicial set X and any topological space Y.
s to be Kan fibration
s. A map of simplicial sets is defined to be a weak equivalence
if the geometric realization is a weak equivalence of spaces. A map of simplicial sets is defined to be a cofibration
if it is a monomorphism
of simplicial sets. It is a difficult theorem of Daniel Quillen that the category of simplicial sets with these classes of morphisms satisfies the axioms for a proper closed simplicial model category
.
A key turning point of the theory is that the realization of a Kan fibration is a Serre fibration of spaces. With the model structure in place, a homotopy theory of simplicial sets can be developed using standard homotopical
abstract nonsense
. Furthermore, the geometric realization and singular functors give a Quillen equivalence
of closed model categories inducing an equivalence of homotopy categories
between the homotopy category for simplicial sets and the usual homotopy category of CW complexes with homotopy classes of maps between them. It is part of the general
definition of a Quillen adjunction that the right adjoint functor (in this case, the singular set functor) carries fibrations (resp. trivial fibrations) to fibrations (resp. trivial fibrations).
or equivalently a covariant functor
When C is the category of sets
, we are just talking about simplicial sets. Letting C be the category of groups
or category of abelian groups
, we obtain the categories sGrp of simplicial group
s and sAb of simplicial abelian group
s, respectively.
Simplicial groups and simplicial abelian groups also carry closed model structures induced by that of the underlying simplicial sets.
The homotopy groups of simplicial abelian groups can be computed by making use of the Dold-Kan correspondence which yields an equivalence of categories between simplicial abelian groups and bounded chain complex
es and is given by functors
and
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a simplicial set is a construction in categorical
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
homotopy theory which is a purely algebraic model of the notion of a "well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
" topological space. Historically, this model arose from earlier work in combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
and in particular from the notion of simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es.
Motivation
A simplicial set is a categorical (that is, purely algebraic) model capturing those topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s which can be built up (or faithfully represented up to homotopy) from simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
and their incidence relations. This is similar to the approach of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es to modeling topological spaces, with the crucial difference that simplicial sets are purely algebraic and do not carry any actual topology (this will become clear in the formal definition).
To get back to actual topological spaces, there is a geometric realization functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
available which takes values in the category of compactly generated Hausdorff spaces. Most classical results on CW complexes in homotopy theory have analogous versions for simplicial sets which generalize these results. While algebraic topologists largely continue to prefer CW complexes, there is a growing contingent of researchers interested in using simplicial sets for applications in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
where CW complexes do not naturally exist.
Formal definition
Using the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a simplicial set X is a contravariant functor
- X: Δ → Set
where Δ denotes the simplex category whose objects are finite strings of ordinal numbers of the form
- n = 0 → 1 → ... → n
(or in other words non-empty totally ordered finite sets) and whose morphisms are order-preserving functions between them, and Set is the category of small sets
Small set (category theory)
In category theory, a small set is one in a fixed universe of sets . Thus, the category of small sets is the category of all sets one cares to consider...
.
It is common to define simplicial sets as a covariant functor from the opposite category
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
, as
- X: Δop → Set
This definition is clearly equivalent to the one immediately above.
Alternatively, one can think of a simplicial set as a simplicial object (see below) in the category Set, but this is only different language for the definition just given. If we use a covariant functor X instead of a contravariant one, we arrive at the definition of a cosimplicial set.
Simplicial sets form a category usually denoted sSet or just S whose objects are simplicial sets and whose morphisms are natural transformations between them. There is a corresponding category for cosimplicial sets as well, denoted by cSet.
These definitions arise from the relationship of the conditions imposed on the face maps and degeneracy maps to the category Δ.
Face and degeneracy maps
In Δop, there are two particularly important classes of maps called face maps and degeneracy maps which capture the underlying combinatorial structure of simplicial sets.The face maps
di :
n
→
n − 1
are given by
- di (0 → … → n) = (0 → … → i − 1 → i + 1 → … → n).
The degeneracy maps
si :
n
→
n + 1
are given by
- si (0 → … → n) = (0 → … → i − 1 → i → i → i + 1 → … → n).
By definition, these maps satisfy the following simplicial identities:
- di dj = dj−1 di if i < j
- di sj = sj−1 di if i < j
- dj sj = id = dj+1 sj
- di sj = sj di−1 if i > j + 1
- si sj = sj+1 si if i ≤ j.
The simplicial category Δ has as its morphisms the monotonic non-decreasing functions. Since the morphisms are generated by those that 'skip' or 'add' a single element, the detailed relations written out above underlie the topological applications. It can be shown that these relations suffice.
The standard n-simplex and the simplex category
Categorically, the standard n-simplex, denoted Δn, is the functor hom(-, n) where n denotes the string 0 → 1 → ... → n of the first (n + 1) nonnegative integers and the homset is taken in the category Δ. In many texts, it is written instead as hom(n,-) where the homset is understood to be in the opposite category Δop.The geometric realization |Δn| is just defined to be the standard topological n-simplex in general position given by
By the Yoneda lemma
Yoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
, the n-simplices of a simplicial set X are classified by natural transformations in hom(Δn, X). The n-simplices of X are then collectively denoted by Xn. Furthermore, there is a simplex category, denoted by
whose objects are maps Δn → X and whose morphisms are natural transformations Δn → Δm over X arising from maps n → m in Δ. The following isomorphism shows that a simplicial set X is a colimit of its simplices:
where the colimit is taken over the simplex category of X.
Geometric realization
There is a functor |•|: S → CGHaus called the geometric realization taking a simplicial set X to its corresponding realization in the category of compactly-generated Hausdorff topological spaces.This larger category is used as the target of the functor because, in particular, a product of simplicial sets
is realized as a product
of the corresponding topological spaces, where
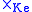denotes the Kelley space product. To define the realization functor, we first define it on n-simplices Δn as the corresponding topological n-simplex |Δn|. The definition then naturally extends to any simplicial set X by setting- |X| = limΔn → X |Δn|
where the colimit is taken over the n-simplex category of X. The geometric realization is functorial on S.
Singular set for a space
The singular set of a topological space Y is the simplicial set defined by S(Y): n → hom(|Δn|, Y) for each object n ∈ Δ, with the obvious functoriality condition on the morphisms. This definition is analogous to a standard idea in singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of "probing" a target topological space with standard topological n-simplices. Furthermore, the singular functor S is right adjoint to the geometric realization functor described above, i.e.:
- homTop(|X|, Y) ≅ homS(X, SY)
for any simplicial set X and any topological space Y.
Homotopy theory of simplicial sets
In the category of simplicial sets one can define fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s to be Kan fibration
Kan fibration
In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial sets. Kan fibrations are the fibrations of the standard model category for simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant objects in this model category...
s. A map of simplicial sets is defined to be a weak equivalence
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
if the geometric realization is a weak equivalence of spaces. A map of simplicial sets is defined to be a cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
if it is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
of simplicial sets. It is a difficult theorem of Daniel Quillen that the category of simplicial sets with these classes of morphisms satisfies the axioms for a proper closed simplicial model category
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
.
A key turning point of the theory is that the realization of a Kan fibration is a Serre fibration of spaces. With the model structure in place, a homotopy theory of simplicial sets can be developed using standard homotopical
Homotopical algebra
In mathematics, homotopical algebra is a collection of concepts comprising the nonabelian aspects of homological algebra as well as possibly the abelian aspects as special cases...
abstract nonsense
Abstract nonsense
In mathematics, abstract nonsense, general abstract nonsense, and general nonsense are terms used facetiously by some mathematicians to describe certain kinds of arguments and methods related to category theory. roughly speaking, category theory is the study of the general form of mathematical...
. Furthermore, the geometric realization and singular functors give a Quillen equivalence
Quillen adjunction
In homotopy theory, a branch of mathematics, a Quillen adjunction between two closed model categories C and D is a special kind of adjunction between categories that induces an adjunction between the homotopy categories Ho and Ho via the total derived functor construction...
of closed model categories inducing an equivalence of homotopy categories
- |•|: Ho(S) ↔ Ho(Top) : S
between the homotopy category for simplicial sets and the usual homotopy category of CW complexes with homotopy classes of maps between them. It is part of the general
definition of a Quillen adjunction that the right adjoint functor (in this case, the singular set functor) carries fibrations (resp. trivial fibrations) to fibrations (resp. trivial fibrations).
Simplicial objects
A simplicial object X in a category C is a contravariant functor- X: Δ → C
or equivalently a covariant functor
- X: Δop → C
When C is the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, we are just talking about simplicial sets. Letting C be the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
or category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, we obtain the categories sGrp of simplicial group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s and sAb of simplicial abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, respectively.
Simplicial groups and simplicial abelian groups also carry closed model structures induced by that of the underlying simplicial sets.
The homotopy groups of simplicial abelian groups can be computed by making use of the Dold-Kan correspondence which yields an equivalence of categories between simplicial abelian groups and bounded chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es and is given by functors
- N: sAb → Ch+
and
- Γ: Ch+ → sAb.
External links
- Dylan G.L. Allegretti, Simplicial Sets and van Kampen's Theorem (An elementary introduction to simplicial sets).