Minimax estimator
Encyclopedia
In statistical decision theory
, where we are faced with the problem of estimating a deterministic parameter (vector) from observations an estimator
(estimation rule) is called minimax
if its maximal risk
is minimal among all estimators of . In a sense this means that is an estimator which performs best in the worst possible case allowed in the problem.
) parameter from noisy or corrupt data related through the conditional probability distribution . Our goal is to find a "good" estimator for estimating the parameter , which minimizes some given risk function
. Here the risk function is the expectation
of some loss function
with respect to . A popular example for a loss function is the squared error loss , and the risk function for this loss is the mean squared error
(MSE). Unfortunately in general the risk cannot be minimized, since it depends on the unknown parameter itself (If we knew what was the actual value of , we wouldn't need to estimate it). Therefore additional criteria for finding an optimal estimator in some sense are required. One such criterion is the minimax criteria.
with respect to a prior least favorable distribution of . To demonstrate this notion denote the average risk of the Bayes estimator with respect to a prior distribution as NEWLINE
falls on "heads" or "tails". In this case the Bayes estimator with respect to a Beta-distributed prior, is NEWLINE
prior, with increasing support and also with respect to a zero mean normal prior with increasing variance. So neither the resulting ML estimator is unique minimax not the least favorable prior is unique. Example 2: Consider the problem of estimating the mean of dimensional Gaussian random vector, . The Maximum likelihood
(ML) estimator for in this case is simply , and it risk is NEWLINE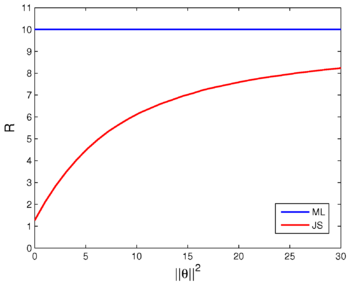 The risk is constant, but the ML estimator is actually not a Bayes estimator, so the Corollary of Theorem 1 does not apply. However, the ML estimator is the limit of the Bayes estimators with respect to the prior sequence , and, hence, indeed minimax according to Theorem 2 . Nonetheless, minimaxity does not always imply admissibility
The risk is constant, but the ML estimator is actually not a Bayes estimator, so the Corollary of Theorem 1 does not apply. However, the ML estimator is the limit of the Bayes estimators with respect to the prior sequence , and, hence, indeed minimax according to Theorem 2 . Nonetheless, minimaxity does not always imply admissibility
. In fact in this example, the ML estimator is known to be inadmissible (not admissible) whenever . The famous James–Stein estimator dominates the ML whenever . Though both estimators have the same risk when , and they are both minimax, the James–Stein estimator has smaller risk for any finite . This fact is illustrated in the following figure.
is known to be minimax whenever . The analytical expression for this estimator is where , is the modified Bessel function
of the first kind of order n.
is an approach to solve optimization problems under uncertainty in the knowledge of underlying parameters,. For instance, the MMSE Bayesian estimation of a parameter requires the knowledge of parameter correlation function. If the knowledge of this correlation function is not perfectly available, a popular minimax robust optimization approach is to define a set characterizing the uncertainty about the correlation function, and then pursuing a minimax optimization over the uncertainty set and the estimator respectively. Similar minimax optimizations can be pursued to make estimators robust to certain imprecisely known parameters. For instance, a recent study dealing with such techniques in the area of signal processing can be found in . In R. Fandom Noubiap and W. Seidel (2001) an algorithm for calculating a Gamma-minimax decision rule has been developed, when Gamma is given by a finite number of generalized moment conditions. Such a decision rule minimizes the maximum of the integrals of the risk function with respect to all distributions in Gamma. Gamma-minimax decision rules are of interest in robustness studies in Bayesian statistics.
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, where we are faced with the problem of estimating a deterministic parameter (vector) from observations an estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
(estimation rule) is called minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
if its maximal risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
is minimal among all estimators of . In a sense this means that is an estimator which performs best in the worst possible case allowed in the problem.
Problem setup
Consider the problem of estimating a deterministic (not BayesianBayes estimator
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...
) parameter from noisy or corrupt data related through the conditional probability distribution . Our goal is to find a "good" estimator for estimating the parameter , which minimizes some given risk function
Risk function
In decision theory and estimation theory, the risk function R of a decision rule, δ, is the expected value of a loss function L:...
. Here the risk function is the expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of some loss function
Loss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
with respect to . A popular example for a loss function is the squared error loss , and the risk function for this loss is the mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
(MSE). Unfortunately in general the risk cannot be minimized, since it depends on the unknown parameter itself (If we knew what was the actual value of , we wouldn't need to estimate it). Therefore additional criteria for finding an optimal estimator in some sense are required. One such criterion is the minimax criteria.
Definition
Definition : An estimator is called minimax with respect to a risk function if it achieves the smallest maximum risk among all estimators, meaning it satisfies NEWLINE- NEWLINE
Least favorable distribution
Logically, an estimator is minimax when it is the best in the worst case. Continuing this logic, a minimax estimator should be a Bayes estimatorBayes estimator
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...
with respect to a prior least favorable distribution of . To demonstrate this notion denote the average risk of the Bayes estimator with respect to a prior distribution as NEWLINE
- NEWLINE
- NEWLINE
- is minimax. NEWLINE
- If is a unique Bayes estimator, it is also the unique minimax estimator. NEWLINE
- is least favorable.
Fair coin
In probability theory and statistics, a sequence of independent Bernoulli trials with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin...
falls on "heads" or "tails". In this case the Bayes estimator with respect to a Beta-distributed prior, is NEWLINE
- NEWLINE
- NEWLINE
- NEWLINE
- is minimax. NEWLINE
- The sequence is least favorable.
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
prior, with increasing support and also with respect to a zero mean normal prior with increasing variance. So neither the resulting ML estimator is unique minimax not the least favorable prior is unique. Example 2: Consider the problem of estimating the mean of dimensional Gaussian random vector, . The Maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
(ML) estimator for in this case is simply , and it risk is NEWLINE
- NEWLINE

Admissible decision rule
In statistical decision theory, an admissible decision rule is a rule for making a decision such that there isn't any other rule that is always "better" than it, in a specific sense defined below....
. In fact in this example, the ML estimator is known to be inadmissible (not admissible) whenever . The famous James–Stein estimator dominates the ML whenever . Though both estimators have the same risk when , and they are both minimax, the James–Stein estimator has smaller risk for any finite . This fact is illustrated in the following figure.
Some examples
In general it is difficult, often even impossible to determine the minimax estimator. Nonetheless, in many cases a minimax estimator has been determined. Example 3, Bounded Normal Mean: When estimating the Mean of a Normal Vector , where it is known that . The Bayes estimator with respect to a prior which is uniformly distributed on the edge of the bounding sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is known to be minimax whenever . The analytical expression for this estimator is where , is the modified Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind of order n.
Relationship to Robust Optimization
Robust optimizationRobust optimization
Robust optimization is a field of optimization theory that deals with optimization problems where robustness is sought against uncertainty and/or variability in the value of a parameter of the problem.- History :...
is an approach to solve optimization problems under uncertainty in the knowledge of underlying parameters,. For instance, the MMSE Bayesian estimation of a parameter requires the knowledge of parameter correlation function. If the knowledge of this correlation function is not perfectly available, a popular minimax robust optimization approach is to define a set characterizing the uncertainty about the correlation function, and then pursuing a minimax optimization over the uncertainty set and the estimator respectively. Similar minimax optimizations can be pursued to make estimators robust to certain imprecisely known parameters. For instance, a recent study dealing with such techniques in the area of signal processing can be found in . In R. Fandom Noubiap and W. Seidel (2001) an algorithm for calculating a Gamma-minimax decision rule has been developed, when Gamma is given by a finite number of generalized moment conditions. Such a decision rule minimizes the maximum of the integrals of the risk function with respect to all distributions in Gamma. Gamma-minimax decision rules are of interest in robustness studies in Bayesian statistics.

