
Mean squared error
Encyclopedia
In statistics
, the mean squared error (MSE) of an estimator
is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function
, corresponding to the expected value of the squared error loss or quadratic loss. MSE measures the average
of the squares of the "errors." The error is the amount by which the value implied by the estimator differs from the quantity to be estimated. The difference occurs because of randomness
or because the estimator doesn't account for information
that could produce a more accurate estimate.
The MSE is the second moment
(about the origin) of the error, and thus incorporates both the variance
of the estimator and its bias
. For an unbiased estimator, the MSE is the variance. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation
, taking the square root of MSE yields the root mean square error or root mean square deviation
(RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard deviation
.
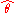 with respect to the estimated parameter
with respect to the estimated parameter 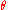 is defined as
is defined as

The MSE is equal to the sum of the variance
and the squared bias
of the estimator
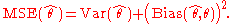
The MSE thus assesses the quality of an estimator in terms of its variation and unbiasedness. Note that the MSE is not equivalent to the expected value of the absolute error.
Since MSE is an expectation, it is not a random variable. It may be a function of the unknown parameter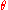 , but it does not depend on any random quantities. However, when MSE is computed for a particular estimator of
, but it does not depend on any random quantities. However, when MSE is computed for a particular estimator of 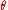 the true value of which is not known, it will be subject to estimation error. In a Bayesian sense, this means that there are cases in which it may be treated as a random variable.
the true value of which is not known, it will be subject to estimation error. In a Bayesian sense, this means that there are cases in which it may be treated as a random variable.
divided by the number of degrees of freedom
. This is an observed quantity given a particular sample (and hence is sample-dependent), whereas the definition above is a function of the parameters of the probability distribution of an unknown parameter. For more details, see errors and residuals in statistics
.
Also in regression analysis, "mean squared error", often referred to as "out-of-sample mean squared error", can refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is an observed quantity, and it varies by sample and by out-of-sample test space.
 . The usual estimator for the mean is the sample average
. The usual estimator for the mean is the sample average
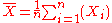
which has an expected value of μ (so it is unbiased) and a mean square error of

For a Gaussian distribution this is the best unbiased estimator (that is, it has the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution
.
The usual estimator for the variance is
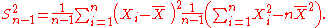
This is unbiased (its expected value is ), and its MSE is
), and its MSE is
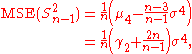
where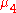 is the fourth central moment
is the fourth central moment
of the distribution or population and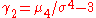 is the excess kurtosis.
is the excess kurtosis.
However, one can use other estimators for which are proportional to
which are proportional to 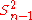 , and an appropriate choice can always give a lower mean square error. If we define
, and an appropriate choice can always give a lower mean square error. If we define
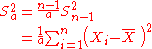
then the MSE is
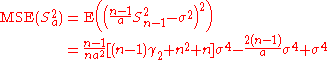
This is minimized when
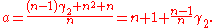
For a Gaussian distribution, where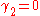 , this means the MSE is minimized when dividing the sum by
, this means the MSE is minimized when dividing the sum by  , whereas for a Bernoulli distribution with p = 1/2 (a coin flip),
, whereas for a Bernoulli distribution with p = 1/2 (a coin flip), 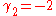 , the MSE is minimized for
, the MSE is minimized for 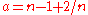 . (Note that this particular case of the Bernoulli distribution has the lowest possible excess kurtosis; this can be proved by Jensen's inequality
. (Note that this particular case of the Bernoulli distribution has the lowest possible excess kurtosis; this can be proved by Jensen's inequality
as follows. The fourth central moment
is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is -2, achieved, for instance, by a Bernoulli with p=1/2.) So no matter what the kurtosis, we get a "better" estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit. Even among unbiased estimators, if the distribution is not Gaussian the best (minimum mean square error) estimator of the variance may not be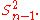
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.
Note that:
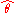 predicts observations of the parameter
predicts observations of the parameter  with perfect accuracy, is the ideal, but is practically never possible.
with perfect accuracy, is the ideal, but is practically never possible.
Values of MSE may be used for comparative purposes. Two or more statistical model
s may be compared using their MSEs as a measure of how well they explain a given set of observations: The unbiased model with the smallest MSE is generally interpreted as best explaining the variability in the observations and is called the best unbiased estimator or MVUE (Minimum Variance Unbiased Estimator).
Both linear regression
techniques such as analysis of variance
estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance
of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
MSE is also used in several stepwise regression
techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
s in statistics, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss
, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds. The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression
, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism
The use of mean squared error without question has been criticized by the decision theorist
James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.
Like variance
, mean squared error has the disadvantage of heavily weighting outliers. This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error
, or those based on the median
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the mean squared error (MSE) of an estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function
Risk function
In decision theory and estimation theory, the risk function R of a decision rule, δ, is the expected value of a loss function L:...
, corresponding to the expected value of the squared error loss or quadratic loss. MSE measures the average
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the squares of the "errors." The error is the amount by which the value implied by the estimator differs from the quantity to be estimated. The difference occurs because of randomness
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
or because the estimator doesn't account for information
Omitted-variable bias
In statistics, omitted-variable bias occurs when a model is created which incorrectly leaves out one or more important causal factors. The 'bias' is created when the model compensates for the missing factor by over- or under-estimating one of the other factors.More specifically, OVB is the bias...
that could produce a more accurate estimate.
The MSE is the second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
(about the origin) of the error, and thus incorporates both the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the estimator and its bias
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
. For an unbiased estimator, the MSE is the variance. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, taking the square root of MSE yields the root mean square error or root mean square deviation
Root mean square deviation
The root-mean-square deviation is the measure of the average distance between the atoms of superimposed proteins...
(RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
Definition and basic properties
The MSE of an estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
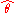 with respect to the estimated parameter
with respect to the estimated parameter 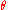 is defined as
is defined as
The MSE is equal to the sum of the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and the squared bias
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
of the estimator
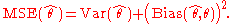
The MSE thus assesses the quality of an estimator in terms of its variation and unbiasedness. Note that the MSE is not equivalent to the expected value of the absolute error.
Since MSE is an expectation, it is not a random variable. It may be a function of the unknown parameter
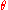 , but it does not depend on any random quantities. However, when MSE is computed for a particular estimator of
, but it does not depend on any random quantities. However, when MSE is computed for a particular estimator of 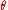 the true value of which is not known, it will be subject to estimation error. In a Bayesian sense, this means that there are cases in which it may be treated as a random variable.
the true value of which is not known, it will be subject to estimation error. In a Bayesian sense, this means that there are cases in which it may be treated as a random variable.Alternative usages
In regression analysis, the term mean squared error is sometimes used to refer to the estimate of error variance: residual sum of squaresResidual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
divided by the number of degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
. This is an observed quantity given a particular sample (and hence is sample-dependent), whereas the definition above is a function of the parameters of the probability distribution of an unknown parameter. For more details, see errors and residuals in statistics
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
.
Also in regression analysis, "mean squared error", often referred to as "out-of-sample mean squared error", can refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is an observed quantity, and it varies by sample and by out-of-sample test space.
Examples
Suppose we have a random sample of size n from a population, . The usual estimator for the mean is the sample average
. The usual estimator for the mean is the sample average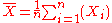
which has an expected value of μ (so it is unbiased) and a mean square error of

For a Gaussian distribution this is the best unbiased estimator (that is, it has the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
.
The usual estimator for the variance is
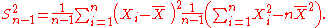
This is unbiased (its expected value is
 ), and its MSE is
), and its MSE is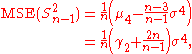
where
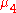 is the fourth central moment
is the fourth central momentCentral moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
of the distribution or population and
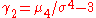 is the excess kurtosis.
is the excess kurtosis.However, one can use other estimators for
 which are proportional to
which are proportional to 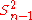 , and an appropriate choice can always give a lower mean square error. If we define
, and an appropriate choice can always give a lower mean square error. If we define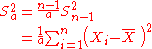
then the MSE is
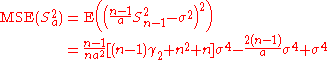
This is minimized when
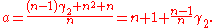
For a Gaussian distribution, where
 , this means the MSE is minimized when dividing the sum by
, this means the MSE is minimized when dividing the sum by  , whereas for a Bernoulli distribution with p = 1/2 (a coin flip),
, whereas for a Bernoulli distribution with p = 1/2 (a coin flip),  , the MSE is minimized for
, the MSE is minimized for 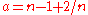 . (Note that this particular case of the Bernoulli distribution has the lowest possible excess kurtosis; this can be proved by Jensen's inequality
. (Note that this particular case of the Bernoulli distribution has the lowest possible excess kurtosis; this can be proved by Jensen's inequalityJensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
as follows. The fourth central moment
Central moment
In probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is -2, achieved, for instance, by a Bernoulli with p=1/2.) So no matter what the kurtosis, we get a "better" estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit. Even among unbiased estimators, if the distribution is not Gaussian the best (minimum mean square error) estimator of the variance may not be
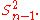
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.
| True value | Estimator | Mean squared error |
|---|---|---|
| θ = μ |  = the unbiased estimator of the population mean, = the unbiased estimator of the population mean, 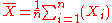 |
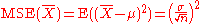 |
| θ = σ2 |  = the unbiased estimator of the population variance, = the unbiased estimator of the population variance, 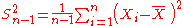 |
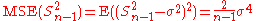 |
| θ = σ2 | 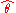 = the biased estimator of the population variance, = the biased estimator of the population variance, 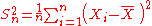 |
 |
| θ = σ2 | 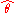 = the biased estimator of the population variance, = the biased estimator of the population variance,  |
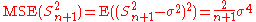 |
Note that:
- The MSEs shown for the variance estimators assume
 i.i.d. so that
i.i.d. so that 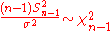 . The result for
. The result for 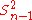 follows easily from the
follows easily from the  variance that is
variance that is  .
. - Unbiased estimators may not produce estimates with the smallest total variation (as measured by MSE): the MSE of
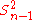 is larger than that of
is larger than that of 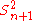 or
or 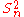 .
. - Estimators with the smallest total variation may produce biased estimates:
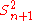 typically underestimates σ2 by
typically underestimates σ2 by 
Interpretation
An MSE of zero, meaning that the estimator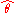 predicts observations of the parameter
predicts observations of the parameter 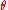 with perfect accuracy, is the ideal, but is practically never possible.
with perfect accuracy, is the ideal, but is practically never possible.Values of MSE may be used for comparative purposes. Two or more statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
s may be compared using their MSEs as a measure of how well they explain a given set of observations: The unbiased model with the smallest MSE is generally interpreted as best explaining the variability in the observations and is called the best unbiased estimator or MVUE (Minimum Variance Unbiased Estimator).
Both linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
techniques such as analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
MSE is also used in several stepwise regression
Stepwise regression
In statistics, stepwise regression includes regression models in which the choice of predictive variables is carried out by an automatic procedure...
techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications
- Minimizing MSE is a key criterion in selecting estimators:see Minimum mean-square errorMinimum mean-square errorIn statistics and signal processing, a minimum mean square error estimator describes the approach which minimizes the mean square error , which is a common measure of estimator quality....
. Among unbiased estimators, the minimal MSE is equivalent to minimizing the variance, and is obtained by the MVUE. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE, representing the difference between the actual observations and the response predicted by the model, is used to determine whether the model does not fit the data or whether the model can be simplified by removing terms.
As a loss function
Squared error loss is one of the most widely used loss functionLoss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
s in statistics, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds. The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism
The use of mean squared error without question has been criticized by the decision theorist
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.
Like variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, mean squared error has the disadvantage of heavily weighting outliers. This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error
Mean absolute error
In statistics, the mean absolute error is a quantity used to measure how close forecasts or predictions are to the eventual outcomes. The mean absolute error is given by...
, or those based on the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
.
See also
- Mean squared prediction error
- Mean square weighted deviationMean square weighted deviationMean square weighted deviation is used extensively in geochronology, the science of obtaining information about the time of formation of, for example, rocks, minerals, bones, corals, or charcoal, or the time at which particular processes took place in a rock mass, for example recrystallization and...
- Mean percentage errorMean Percentage ErrorIn statistics, the mean percentage error is the computed average of percentage errors by which estimated forecasts differ from actual values of the quantity being forecast.Formula for mean percentage error calculation is:...
- Squared deviationsSquared deviationsIn probability theory and statistics, the definition of variance is either the expected value , or average value , of squared deviations from the mean. Computations for analysis of variance involve the partitioning of a sum of squared deviations...
- Peak signal-to-noise ratioPeak signal-to-noise ratioThe phrase peak signal-to-noise ratio, often abbreviated PSNR, is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation...
- Root mean square deviationRoot mean square deviationThe root-mean-square deviation is the measure of the average distance between the atoms of superimposed proteins...

