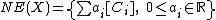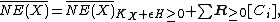Cone of curves
Encyclopedia
In mathematics
, the cone of curves (sometimes the Kleiman-Mori cone) of an algebraic variety
 is a combinatorial invariant of much importance to the birational geometry
is a combinatorial invariant of much importance to the birational geometry
of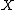 .
.
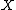 be a proper variety. By definition, a (real) 1-cycle on
be a proper variety. By definition, a (real) 1-cycle on 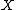 is a formal linear combination
is a formal linear combination
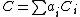 of irreducible, reduced and proper curves
of irreducible, reduced and proper curves 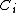 , with coefficients
, with coefficients 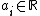 . Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles
. Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles 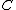 and
and 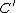 are numerically equivalent if
are numerically equivalent if 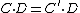 for every Cartier divisor
for every Cartier divisor
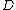 on
on 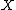 . Denote the real vector space of 1-cycles modulo numerical equivalence by
. Denote the real vector space of 1-cycles modulo numerical equivalence by 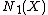 .
.
We define the cone of curves of to be
to be
where the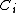 are irreducible, reduced, proper curves on
are irreducible, reduced, proper curves on 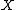 , and
, and 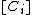 their classes in
their classes in 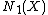 . It is not difficult to see that
. It is not difficult to see that 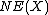 is indeed a convex cone in the sense of convex geometry.
is indeed a convex cone in the sense of convex geometry.
condition, which says that a (Cartier) divisor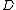 on a complete variety
on a complete variety 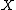 is ample
is ample
if and only if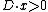 for any nonzero element
for any nonzero element  in
in 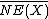 , the closure of the cone of curves in the usual real topology. (In general,
, the closure of the cone of curves in the usual real topology. (In general, 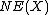 need not be closed, so taking the closure here is important.)
need not be closed, so taking the closure here is important.)
A more involved example is the role played by the cone of curves in the theory of minimal model
s of algebraic varieties. Briefly, the goal of that theory is as follows: given a (mildly singular) projective variety , find a (mildly singular) variety
, find a (mildly singular) variety  which is birational to
which is birational to 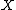 , and whose canonical divisor
, and whose canonical divisor 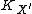 is nef
is nef
. The great breakthrough of the early 1980s (due to Mori
and others) was to construct (at least morally) the necessary birational map from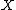 to
to  as a sequence of steps, each of which can be thought of as contraction of a
as a sequence of steps, each of which can be thought of as contraction of a 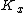 -negative extremal ray of
-negative extremal ray of  . This process encounters difficulties, however, whose resolution necessitates the introduction of the flip
. This process encounters difficulties, however, whose resolution necessitates the introduction of the flip
.
; it was later generalised to a larger class of varieties by Kollár, Reid, Shokurov, and others. Mori's version of the theorem is as follows:
Cone Theorem. Let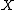 be a smooth projective variety. Then
be a smooth projective variety. Then
1. There are countably many rational curves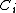 on
on 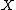 , satisfying
, satisfying 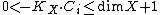 , and
, and
2. For any positive real number and any ample divisor
and any ample divisor 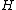 ,
,
where the sum in the last term is finite.
The first assertion says that, in the closed half-space of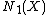 where intersection with
where intersection with 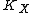 is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rational
is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rational
, and their 'degree' is bounded very tightly by the dimension of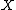 . The second assertion then tells us more: it says that, away from the hyperplane
. The second assertion then tells us more: it says that, away from the hyperplane 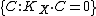 , extremal rays of the cone cannot accumulate.
, extremal rays of the cone cannot accumulate.
If in addition the variety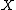 is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:
is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:
3. Let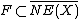 be an extremal face of the cone of curves on which
be an extremal face of the cone of curves on which 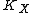 is negative. Then there is a unique morphism
is negative. Then there is a unique morphism
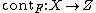 to a projective variety Z, such that
to a projective variety Z, such that 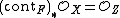 and an irreducible curve
and an irreducible curve 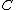 in
in 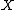 is mapped to a point by
is mapped to a point by 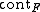 if and only if
if and only if 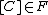 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the cone of curves (sometimes the Kleiman-Mori cone) of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
 is a combinatorial invariant of much importance to the birational geometry
is a combinatorial invariant of much importance to the birational geometryBirational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
of
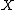 .
.Definition
Let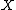 be a proper variety. By definition, a (real) 1-cycle on
be a proper variety. By definition, a (real) 1-cycle on 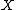 is a formal linear combination
is a formal linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
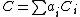 of irreducible, reduced and proper curves
of irreducible, reduced and proper curves 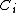 , with coefficients
, with coefficients 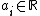 . Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles
. Numerical equivalence of 1-cycles is defined by intersections: two 1-cycles 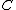 and
and 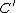 are numerically equivalent if
are numerically equivalent if 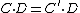 for every Cartier divisor
for every Cartier divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
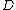 on
on 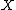 . Denote the real vector space of 1-cycles modulo numerical equivalence by
. Denote the real vector space of 1-cycles modulo numerical equivalence by 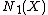 .
.We define the cone of curves of
 to be
to bewhere the
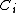 are irreducible, reduced, proper curves on
are irreducible, reduced, proper curves on 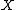 , and
, and 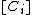 their classes in
their classes in 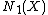 . It is not difficult to see that
. It is not difficult to see that 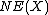 is indeed a convex cone in the sense of convex geometry.
is indeed a convex cone in the sense of convex geometry.Applications
One useful application of the notion of the cone of curves is the KleimanSteven Kleiman
Steven Lawrence Kleiman is an American mathematician.He is a Professor of Mathematics at the Massachusetts Institute of Technology. Born in Boston, he did his undergraduate studies at the MIT. He received his Ph.D. from Harvard University in 1965, after studying there with Oscar Zariski and David...
condition, which says that a (Cartier) divisor
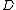 on a complete variety
on a complete variety 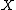 is ample
is ampleAmple line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
if and only if
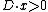 for any nonzero element
for any nonzero element  in
in 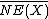 , the closure of the cone of curves in the usual real topology. (In general,
, the closure of the cone of curves in the usual real topology. (In general, 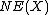 need not be closed, so taking the closure here is important.)
need not be closed, so taking the closure here is important.)A more involved example is the role played by the cone of curves in the theory of minimal model
Minimal model
*In theoretical physics, the term minimal model usually refers to a special class of conformal field theories that generalize the Ising model, or to some closely related representations of the Virasoro algebra...
s of algebraic varieties. Briefly, the goal of that theory is as follows: given a (mildly singular) projective variety
 , find a (mildly singular) variety
, find a (mildly singular) variety  which is birational to
which is birational to 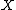 , and whose canonical divisor
, and whose canonical divisor 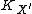 is nef
is nefNumerically effective
A line bundle on an algebraic variety is said to be nef , if the degree of the restriction to any algebraic curve of the variety is non-negative.In particular, every ample line bundle is nef....
. The great breakthrough of the early 1980s (due to Mori
Shigefumi Mori
-References:*Heisuke Hironaka, Fields Medallists Lectures, Michael F. Atiyah , Daniel Iagolnitzer ; World Scientific Publishing, 2007. ISBN 9810231172...
and others) was to construct (at least morally) the necessary birational map from
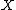 to
to  as a sequence of steps, each of which can be thought of as contraction of a
as a sequence of steps, each of which can be thought of as contraction of a 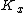 -negative extremal ray of
-negative extremal ray of  . This process encounters difficulties, however, whose resolution necessitates the introduction of the flip
. This process encounters difficulties, however, whose resolution necessitates the introduction of the flipFlip (algebraic geometry)
In algebraic geometry, flips and flops are codimension-2 surgery operations arising in the minimal model program, given by blowing up along a relative canonical ring. In dimension 3 flips are used to construct minimal models, and any two birationally equivalent minimal models are connected by...
.
A structure theorem
The above process of contractions could not proceed without the fundamental result on the structure of the cone of curves known as the Cone Theorem. The first version of this theorem, for smooth varieties, is due to MoriShigefumi Mori
-References:*Heisuke Hironaka, Fields Medallists Lectures, Michael F. Atiyah , Daniel Iagolnitzer ; World Scientific Publishing, 2007. ISBN 9810231172...
; it was later generalised to a larger class of varieties by Kollár, Reid, Shokurov, and others. Mori's version of the theorem is as follows:
Cone Theorem. Let
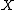 be a smooth projective variety. Then
be a smooth projective variety. Then1. There are countably many rational curves
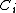 on
on 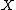 , satisfying
, satisfying 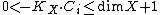 , and
, and2. For any positive real number
 and any ample divisor
and any ample divisor 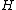 ,
,where the sum in the last term is finite.
The first assertion says that, in the closed half-space of
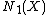 where intersection with
where intersection with 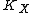 is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rational
is nonnegative, we know nothing, but in the complementary half-space, the cone is spanned by some countable collection of curves which are quite special: they are rationalRational variety
In mathematics, a rational variety is an algebraic variety, over a given field K, which is birationally equivalent to projective space of some dimension over K...
, and their 'degree' is bounded very tightly by the dimension of
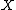 . The second assertion then tells us more: it says that, away from the hyperplane
. The second assertion then tells us more: it says that, away from the hyperplane 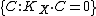 , extremal rays of the cone cannot accumulate.
, extremal rays of the cone cannot accumulate.If in addition the variety
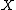 is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:
is defined over a field of characteristic 0, we have the following assertion, sometimes referred to as the Contraction Theorem:3. Let
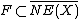 be an extremal face of the cone of curves on which
be an extremal face of the cone of curves on which 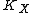 is negative. Then there is a unique morphism
is negative. Then there is a unique morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
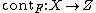 to a projective variety Z, such that
to a projective variety Z, such that 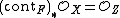 and an irreducible curve
and an irreducible curve 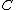 in
in 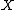 is mapped to a point by
is mapped to a point by 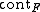 if and only if
if and only if 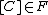 .
.