Metaplectic structure
Encyclopedia
In differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifold
s. A metaplectic structure on a symplectic manifold
allows one to define the symplectic spinor bundle, which is the Hilbert space
bundle associated to the metaplectic structure via the metaplectic representation, giving rise to the notion of a symplectic spinor field in differential geometry.
Symplectic spin structures have wide applications to mathematical physics
, in particular to quantum field theory
where they are an essential ingredient in establishing the idea that symplectic spin geometry and symplectic Dirac operators may give valuable tools in symplectic geometry and symplectic topology. They are also of purely mathematical interest in differential geometry, algebraic topology
, and K theory. They form the foundation for symplectic spin geometry.
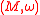is an equivariant
lift of the symplectic frame bundle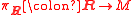
with respect to the double covering 
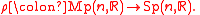In other words, a pair 
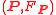is a metaplectic structure on the principal bundle 
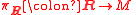when
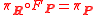and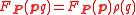 
for all 
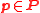and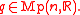 
The principal bundle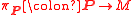
is also called the bundle of metaplectic frames over 
.
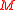Two metaplectic structures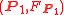
and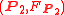 
on the same symplectic manifold
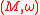are called equivalent if there exists a 
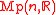-equivariant map 
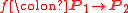such that
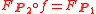and 
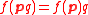for all 
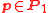and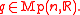 
Of course, in this case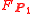
and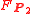 
are two equivalent double coverings of the symplectic frame 
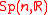-bundle 
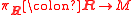of the given symplectic manifold 
.
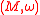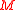is necessarily of even dimension and orientable, one can prove that the topological obstruction
to the existence of metaplectic structures is precisely the same as in Riemannian spin geometry
. In other words, a symplectic manifold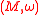
admits a metaplectic structures if and only if the second Stiefel-Whitney class 
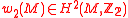of 
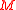vanishes. If this is the case, the isomorphy classes of metaplectic structures on 
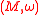are classified by the first cohomology group 
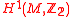of 
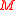with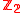 
-coefficients. As the manifold 
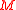is assumed to be oriented, the first Stiefel-Whitney class 
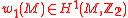of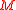 
vanishes too.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. A metaplectic structure on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
allows one to define the symplectic spinor bundle, which is the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
bundle associated to the metaplectic structure via the metaplectic representation, giving rise to the notion of a symplectic spinor field in differential geometry.
Symplectic spin structures have wide applications to mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, in particular to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where they are an essential ingredient in establishing the idea that symplectic spin geometry and symplectic Dirac operators may give valuable tools in symplectic geometry and symplectic topology. They are also of purely mathematical interest in differential geometry, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, and K theory. They form the foundation for symplectic spin geometry.
Formal definition
A metaplectic structure on a symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
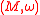is an equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
lift of the symplectic frame bundle
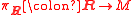with respect to the double covering 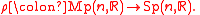In other words, a pair 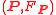is a metaplectic structure on the principal bundle 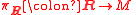when
- a)
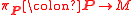is a principal 
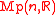-bundle over 
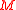, - b)
is an equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
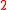-fold covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
such that
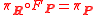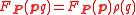and for all 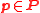and 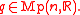The principal bundle
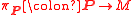is also called the bundle of metaplectic frames over 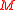.Two metaplectic structures
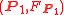and 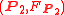on the same symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
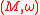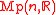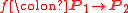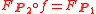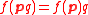are called equivalent if there exists a -equivariant map such that and for all 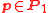and 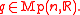Of course, in this case
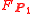and 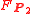are two equivalent double coverings of the symplectic frame 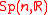-bundle 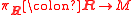of the given symplectic manifold 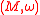.Obstruction
Since every symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
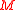is necessarily of even dimension and orientable, one can prove that the topological obstructionObstruction
Obstruction may refer to:* Obstruction theory, in mathematics* Obstruction of justice, the crime of interfering with law enforcement* Obstructing government administration* Propagation path obstruction** Single Vegetative Obstruction Model-Medical:...
to the existence of metaplectic structures is precisely the same as in Riemannian spin geometry
Spin geometry
Spin geometry is the area of differential geometry and topology where objects like spin manifoldsand Dirac operators, and the various associated index theorems have come to play a fundamental role both in mathematics and in mathematical physics....
. In other words, a symplectic manifold
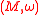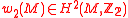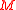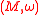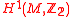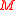admits a metaplectic structures if and only if the second Stiefel-Whitney class of vanishes. If this is the case, the isomorphy classes of metaplectic structures on are classified by the first cohomology group of with 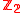-coefficients. As the manifold 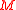is assumed to be oriented, the first Stiefel-Whitney class 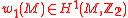of 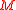vanishes too.Manifolds admitting a metaplectic structure
- Phase spaces
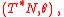
any orientable manifold. - Complex projective spaces
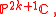
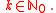Since 
is simply connected, such a structure has to be unique. - Grassmannian
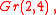e.t.c.
See also
- Metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
- Symplectic frame bundle
- Symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
- Symplectic spinor bundle