In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

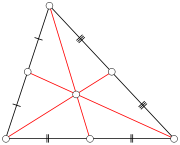
, a median of a triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 is a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 joining a vertex

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 to the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

 of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side. The median bisects the vertex angle from which it is drawn in case of isosceles and equilateral

Equilateral

In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...

 triangles.

Relation to center of mass

Each median of a triangle passes through the triangle's centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

, which is the center of mass of an object of uniform density in the shape of the triangle. Thus the object would balance on any line through the centroid, including any median.

Equal-area division

Each median divides the area of the triangle in half; hence the name. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.)http://www.btinternet.com/~se16/js/halfarea.htm The three medians divide the triangle into six smaller triangles of equal area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

.

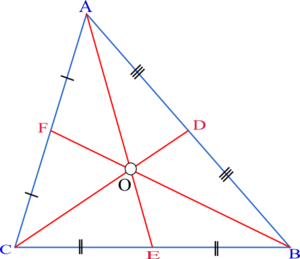
Proof

Consider a triangle ABC Let D be the midpoint of , E be the midpoint of , F be the midpoint of , and O be the centroid.

By definition, 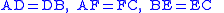. Thus 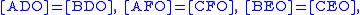and 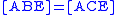, where represents the area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 of triangle ; these hold because in each case the two triangles have bases of equal length and share a common altitude from the (extended) base, and a triangle's area equals one-half its base times its height.

We have:


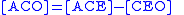
Thus, 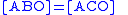and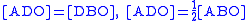

Since 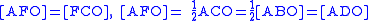, therefore, .
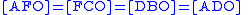Using the same method, you can show that .

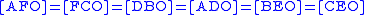Formulas involving the medians' lengths

The lengths of the medians can be obtained from Apollonius' theorem

Apollonius' theorem

In geometry, Apollonius' theorem is a theorem relating the length of a median of a triangle to the lengths of its side.Specifically, in any triangle ABC, if AD is a median, thenAB^2 + AC^2 = 2\,...

 as:




where a, b and c are the sides of the triangle with respective medians m_a, m_b, and m_c from their midpoints.

Thus we have the relationships:

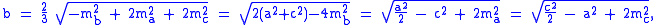
Other properties

For any triangle,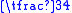
(perimeter) < sum of the medians < (perimeter).

For any triangle with sides 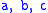and medians ,

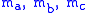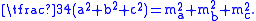
External links

• Medians and Area Bisectors of a Triangle
• The Medians at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Area of Median Triangle at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Medians of a triangle With interactive animation
• Constructing a median of a triangle with compass and straightedge animated demonstration