Mapping cone (homological algebra)
Encyclopedia
In homological algebra
, the mapping cone is a construction on a map of chain complexes inspired by the analogous construction in topology
. In the theory of triangulated categories it is a kind of combined kernel
and cokernel
: if the chain complexes take their terms in an abelian category
, so that we can talk about cohomology
, then the cone of a map f being acyclic
means that the map is a quasi-isomorphism
; if we pass to the derived category
of complexes, this means that f is an isomorphism there, which recalls the familiar property of maps of group
s, modules over a ring
, or elements of an arbitrary abelian category that if the kernel and cokernel both vanish, then the map is an isomorphism. If we are working in a t-category, then in fact the cone furnishes both the kernel and cokernel of maps between objects of its core.
(i.e., a category whose morphisms form abelian groups and in which we may construct a direct sum
of any two objects). Let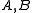
be two complexes, with differentials 
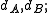i.e.,
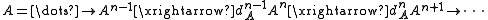
and likewise for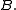
For a map of complexes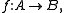
we define the cone, often denoted by 
or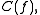 
to be the following complex:
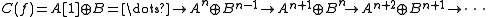on terms,
with differential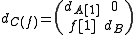
(acting as though on column vectors).
Here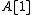
is the complex with 
and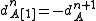 
.
Note that the differential on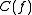
is different from the natural differential on 
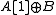, and that some authors use a different sign convention.
Thus, if for example our complexes are of abelian groups, the differential would act as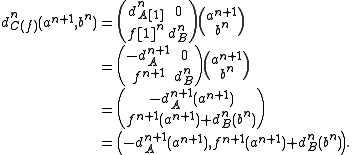
, so that the cohomology
of a complex is defined. The main use of the cone is to identify quasi-isomorphism
s: if the cone is acyclic
, then the map is a quasi-isomorphism. To see this, we use the existence of a triangle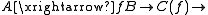
where the maps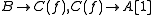
are the projections onto the direct summands (see Homotopy category of chain complexes
). Since this is a triangle, it gives rise to a long exact sequence on cohomology groups: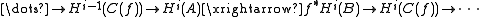
and if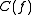
is acyclic then by definition, the outer terms above are zero. Since the sequence is exact, this means that 
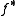induces an isomorphism on all cohomology groups, and hence (again by definition) is a quasi-isomorphism.
This fact recalls the usual alternative characterization of isomorphisms in an abelian category
as those maps whose kernel and cokernel both vanish. This appearance of a cone as a combined kernel and cokernel is not accidental; in fact, under certain circumstances the cone literally embodies both. Say for example that we are working over an abelian category and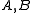
have only one nonzero term in degree 0: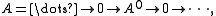
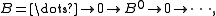
and therefore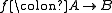
is just 
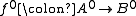(as a map of objects of the underlying abelian category). Then the cone is just
(Underset text indicates the degree of each term.) The cohomology of this complex is then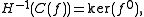
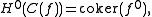
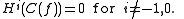
This is not an accident and in fact occurs in every t-category.
of a continuous map of topological space
s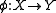
: the complex of singular chains
of the topological cone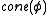
is homotopy equivalent to the cone (in the chain-complex-sense) of the induced map of singular chains of X to Y. The mapping cylinder of a map of complexes is similarly related to the mapping cylinder
of continuous maps.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the mapping cone is a construction on a map of chain complexes inspired by the analogous construction in topology
Mapping cone
In mathematics, especially homotopy theory, the mapping cone is a construction C_f of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated Cf.-Definition:...
. In the theory of triangulated categories it is a kind of combined kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
: if the chain complexes take their terms in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, so that we can talk about cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
, then the cone of a map f being acyclic
Acyclic
Acyclic can refer to:* In chemistry, a compound which is not cyclic, e.g. alkanes and acyclic aliphatic compounds* In mathematics:** A graph without a cycle, especially*** A directed acyclic graph...
means that the map is a quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
; if we pass to the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of complexes, this means that f is an isomorphism there, which recalls the familiar property of maps of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, modules over a ring
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, or elements of an arbitrary abelian category that if the kernel and cokernel both vanish, then the map is an isomorphism. If we are working in a t-category, then in fact the cone furnishes both the kernel and cokernel of maps between objects of its core.
Definition
The cone may be defined in the category of chain complexes over any additive categoryAdditive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
(i.e., a category whose morphisms form abelian groups and in which we may construct a direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of any two objects). Let
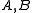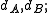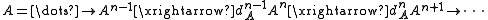
be two complexes, with differentials i.e.,and likewise for
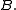
For a map of complexes
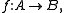we define the cone, often denoted by or 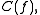to be the following complex: 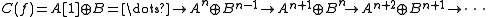on terms,with differential
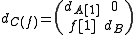(acting as though on column vectors).Here
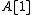is the complex with and 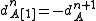.Note that the differential on
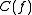is different from the natural differential on 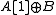, and that some authors use a different sign convention.Thus, if for example our complexes are of abelian groups, the differential would act as
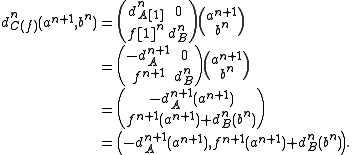
Properties
Suppose now that we are working over an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, so that the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of a complex is defined. The main use of the cone is to identify quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
s: if the cone is acyclic
Acyclic
Acyclic can refer to:* In chemistry, a compound which is not cyclic, e.g. alkanes and acyclic aliphatic compounds* In mathematics:** A graph without a cycle, especially*** A directed acyclic graph...
, then the map is a quasi-isomorphism. To see this, we use the existence of a triangle
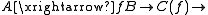
where the maps
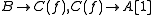are the projections onto the direct summands (see Homotopy category of chain complexesHomotopy category of chain complexes
In homological algebra in mathematics, the homotopy category K of chain complexes in an additive category A is a framework for working with chain homotopies and homotopy equivalences...
). Since this is a triangle, it gives rise to a long exact sequence on cohomology groups:
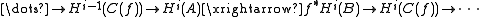
and if
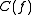is acyclic then by definition, the outer terms above are zero. Since the sequence is exact, this means that 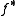induces an isomorphism on all cohomology groups, and hence (again by definition) is a quasi-isomorphism.This fact recalls the usual alternative characterization of isomorphisms in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
as those maps whose kernel and cokernel both vanish. This appearance of a cone as a combined kernel and cokernel is not accidental; in fact, under certain circumstances the cone literally embodies both. Say for example that we are working over an abelian category and
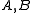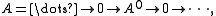
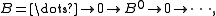
have only one nonzero term in degree 0:and therefore
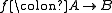is just 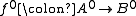(as a map of objects of the underlying abelian category). Then the cone is just(Underset text indicates the degree of each term.) The cohomology of this complex is then
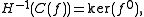
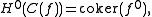
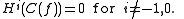
This is not an accident and in fact occurs in every t-category.
Mapping cylinder
A related notion is the mapping cylinder: let f: A → B be a morphism of complexes, let further g : Cone(f)[-1] → A be the natural map. The mapping cylinder of f is by definition the mapping cone of g.Topological inspiration
This complex is called the cone in analogy to the mapping coneMapping cone
In mathematics, especially homotopy theory, the mapping cone is a construction C_f of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated Cf.-Definition:...
of a continuous map of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s
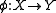: the complex of singular chainsSingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of the topological cone
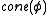is homotopy equivalent to the cone (in the chain-complex-sense) of the induced map of singular chains of X to Y. The mapping cylinder of a map of complexes is similarly related to the mapping cylinderMapping cylinder
In mathematics, specifically algebraic topology, the mapping cylinder of a function f between topological spaces X and Y is the quotientM_f = \,/\,\sim...
of continuous maps.