Magnetic flux
Encyclopedia
Magnetic flux is a measure of the amount of magnetic B field
(also called "magnetic flux density") passing through a given surface (such as a conducting coil). The SI
unit of magnetic flux is the weber
(Wb) (in derived units: volt-seconds). The CGS
unit is the maxwell
.
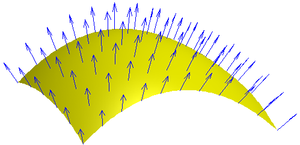The magnetic flux through a given surface is proportional to the number of magnetic B field lines that pass through the surface. This is the net number, i.e. the number passing through in one direction, minus the number passing through in the other direction. (See below for how the positive sign is chosen.) For a uniform magnetic field B passing through a perpendicular
area
the magnetic flux is given by the product of the magnetic field
and the area
element. The magnetic flux for a uniform B at any angle to a surface is defined by a dot product
of the magnetic field and the area element vector a.
(uniform B with flat area only)
where θ is the angle between B and a vector a that is perpendicular (normal) to the surface.
In the general case, the magnetic flux through a surface S is defined as the integral
of the magnetic field over the area of the surface (See Figures 1 and 2):
where
is the magnetic flux, B is the magnetic field,
From the definition of the magnetic vector potential A and the fundamental theorem of the curl
the magnetic flux may also be defined as:
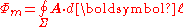
where the closed line integral
is over the boundary of the surface and dℓ is an infinitesimal
vector element of that contour Σ.
The magnetic flux is usually measured with a fluxmeter. The fluxmeter contains measuring coils and electronics that evaluates the change of voltage in the measuring coils to calculate the magnetic flux.
, states that the total magnetic flux through a closed surface is equal to zero. (A "closed surface" is a surface that completely encloses a volume(s) with no holes.) This law is a consequence of the empirical observation that magnetic monopole
s have never been found.
In other words, Gauss's law for magnetism is the statement:
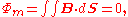
for any closed surface S.
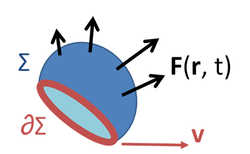While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface need not be zero and is an important quantity in electromagnetism. For example, a change in the magnetic flux passing through a loop of conductive wire will cause an electromotive force
, and therefore an electric current, in the loop. The relationship is given by Faraday's law
:
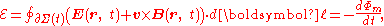
where (see Figure 3):
The EMF is determined in this equation in two ways: first, as the work per unit charge done against the Lorentz force
in moving a test charge around the (possibly moving) closed curve ∂Σ(t), and second, as the magnetic flux through the open surface Σ(t).
This equation is the principle behind an electrical generator
.
, another of Maxwell's equations
, is
where
Note that the flux of E through a closed surface is not always zero; this indicates the presence of electric "monopoles", that is, free positive or negative charges.
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
(also called "magnetic flux density") passing through a given surface (such as a conducting coil). The SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of magnetic flux is the weber
Weber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
(Wb) (in derived units: volt-seconds). The CGS
Centimetre gram second system of units
The centimetre–gram–second system is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time...
unit is the maxwell
Maxwell (unit)
The maxwell, abbreviated as Mx, is the compound derived CGS unit of magnetic flux. The unit was previously called a line. The unit name honours James Clerk Maxwell, who presented the unified theory of electromagnetism, and was established by the IEC in 1930.In a magnetic field of strength one...
.
Description
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
the magnetic flux is given by the product of the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
element. The magnetic flux for a uniform B at any angle to a surface is defined by a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the magnetic field and the area element vector a.
(uniform B with flat area only)where θ is the angle between B and a vector a that is perpendicular (normal) to the surface.
In the general case, the magnetic flux through a surface S is defined as the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the magnetic field over the area of the surface (See Figures 1 and 2):
where
is the magnetic flux, B is the magnetic field,
- S is the surface (area),
denotes dot product, and dS is an infinitesimal vector, whose magnitude is the area of a differential element of S, and whose direction is the surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
. (See surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
for more details.)
From the definition of the magnetic vector potential A and the fundamental theorem of the curl
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
the magnetic flux may also be defined as:
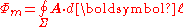
where the closed line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
is over the boundary of the surface and dℓ is an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
vector element of that contour Σ.
The magnetic flux is usually measured with a fluxmeter. The fluxmeter contains measuring coils and electronics that evaluates the change of voltage in the measuring coils to calculate the magnetic flux.
Magnetic flux through a closed surface
Gauss's law for magnetism, which is one of the four Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, states that the total magnetic flux through a closed surface is equal to zero. (A "closed surface" is a surface that completely encloses a volume(s) with no holes.) This law is a consequence of the empirical observation that magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s have never been found.
In other words, Gauss's law for magnetism is the statement:
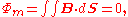
for any closed surface S.
Magnetic flux through an open surface
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
, and therefore an electric current, in the loop. The relationship is given by Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
:
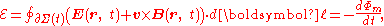
where (see Figure 3):
is the EMFElectromotive forceIn physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
,- Φm is the flux through a surface with an opening bounded by a curve ∂Σ(t),
- ∂Σ(t) is a closed contour that can change with time; the EMF is found around this contour, and the contour is a boundary of the surface over which Φm is found,
- dℓ is an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
vector element of the contour ∂Σ(t), - v is the velocity of the segment dℓ,
- E is the electric field,
- B is the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
.
The EMF is determined in this equation in two ways: first, as the work per unit charge done against the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
in moving a test charge around the (possibly moving) closed curve ∂Σ(t), and second, as the magnetic flux through the open surface Σ(t).
This equation is the principle behind an electrical generator
Electrical generator
In electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
.
Comparison with electric flux
By way of contrast, Gauss's law for electric fieldsGauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
, another of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, is
where
- E is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, - S is any closed surface,
- Q is the total electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
inside the surface S,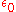
is the electric constantElectric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
(a universal constant, also called the "permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of free space").
Note that the flux of E through a closed surface is not always zero; this indicates the presence of electric "monopoles", that is, free positive or negative charges.
See also
- Magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
(sometimes called the Maxwell equations) are the set of four equations, attributed to James Clerk Maxwell, that describe the behavior of both the electric and magnetic fields, as well as their interactions with matter. - Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
gives the relation between the electric flux flowing out a closed surface and the electric charge enclosed in the surface. - Magnetic circuitMagnetic circuitA magnetic circuit is made up of one or more closed loop paths containing a magnetic flux. The flux is usually generated by permanent magnets or electromagnets and confined to the path by magnetic cores consisting of ferromagnetic materials like iron, although there may be air gaps or other...
is a method using an analogy with electric circuits to calculate the flux of complex systems of magnetic components. - Magnetic monopoleMagnetic monopoleA magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
is a hypothetical particle that may be loosely described as "a magnet with only one pole". - Magnetic flux quantumMagnetic flux quantumThe magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
is the quantum of magnetic flux passing through a superconductor. - Carl Friedrich GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
developed a fruitful collaboration with the physics professor Wilhelm Weber; it led to new knowledge in the field of magnetism. - James Clerk MaxwellJames Clerk MaxwellJames Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
demonstrated that electric and magnetic forces are two complementary aspects of electromagnetism.
External articles
Patents- Vicci, , Magnetic-flux conduits
- Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB - Tape Operating Levels and Tape Alignment Levels