Liouville's theorem (differential algebra)
Encyclopedia
In mathematics
, Liouville's theorem, originally formulated by Joseph Liouville
in the 1830s and 1840s, places an important restriction on antiderivative
s that can be expressed as elementary functions.
The antiderivatives of certain elementary functions cannot themselves be expressed as elementary functions. A standard example of such a function is
whose antiderivative is (up to constants) the error function
, familiar from statistics
. Other examples include the functions
and 
Liouville's theorem states that elementary antiderivatives, if they exist, must be in the same differential field as the function, plus possibly a finite number of logarithms.
called the constants of F. Given two differential fields F and G, G is called a logarithmic extension of F if G is a simple transcendental extension
of F (i.e. G = F(t) for some transcendental t) such that
This has the form of a logarithmic derivative
. Intuitively, one may think of t as the logarithm
of some element s of F, in which case, this condition is analogous to the ordinary chain rule
. But it must be remembered that F is not necessarily equipped with a unique logarithm; one might adjoin many "logarithm-like" extensions to F. Similarly, an exponential extension is a simple transcendental extension that satisfies
With the above caveat in mind, this element may be thought of as an exponential of an element s of F. Finally, G is called an elementary differential extension of F if there is a finite chain of subfields from F to G where each extension in the chain is either algebraic, logarithmic, or exponential.
In other words, the only functions that have "elementary antiderivatives" (i.e. antiderivatives living in, at worst, an elementary differential extension of F) are those with this form prescribed by the theorem. Thus, on an intuitive level, the theorem states that the only elementary antiderivatives are the "simple" functions plus a finite number of logarithms of "simple" functions.
A proof of Liouville's theorem can be found in section 12.4 of Geddes, et al.
s in a single variable has a derivation given by the standard derivative
with respect to that variable. The constants of this field are just the complex number
s C.
The function
, which exists in C(x), does not have an antiderivative in C(x). Its antiderivatives ln x + C do, however, exist in the logarithmic extension C(x, ln x).
Likewise, the function
does not have an antiderivative in C(x). Its antiderivatives tan−1(x) + C do not seem to satisfy the requirements of the theorem, since they are not (apparently) sums of rational functions and logarithms of rational functions. However, a calculation with Euler's formula
shows that in fact the antiderivatives can be written in the required manner (as logarithms of rational functions).
, but this is not strictly true. The theorem can be proved without any use of Galois theory. Furthermore, the Galois group of a simple antiderivative is either trivial (if no field extension is required to express it), or is simply the additive group of the constants (corresponding to the constant of integration). Thus, an antiderivative's differential Galois group does not encode enough information to determine if it can be expressed using elementary functions, the major condition of Liouville's theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Liouville's theorem, originally formulated by Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
in the 1830s and 1840s, places an important restriction on antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s that can be expressed as elementary functions.
The antiderivatives of certain elementary functions cannot themselves be expressed as elementary functions. A standard example of such a function is
whose antiderivative is (up to constants) the error functionError function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
, familiar from statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. Other examples include the functions
and 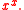Liouville's theorem states that elementary antiderivatives, if they exist, must be in the same differential field as the function, plus possibly a finite number of logarithms.
Definitions
For any differential field F, there is a subfield- Con(F) = {f in F | Df = 0},
called the constants of F. Given two differential fields F and G, G is called a logarithmic extension of F if G is a simple transcendental extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of F (i.e. G = F(t) for some transcendental t) such that
- Dt = Ds/s for some s in F.
This has the form of a logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
. Intuitively, one may think of t as the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of some element s of F, in which case, this condition is analogous to the ordinary chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. But it must be remembered that F is not necessarily equipped with a unique logarithm; one might adjoin many "logarithm-like" extensions to F. Similarly, an exponential extension is a simple transcendental extension that satisfies
- Dt = t Ds.
With the above caveat in mind, this element may be thought of as an exponential of an element s of F. Finally, G is called an elementary differential extension of F if there is a finite chain of subfields from F to G where each extension in the chain is either algebraic, logarithmic, or exponential.
Basic theorem
Suppose F and G are differential fields, with Con(F) = Con(G), and that G is an elementary differential extension of F. Let a be in F, y in G, and suppose Dy = a (in words, suppose that G contains an antiderivative of a). Then there exist c1, ..., cn in Con(F), u1, ..., un, v in F such thatIn other words, the only functions that have "elementary antiderivatives" (i.e. antiderivatives living in, at worst, an elementary differential extension of F) are those with this form prescribed by the theorem. Thus, on an intuitive level, the theorem states that the only elementary antiderivatives are the "simple" functions plus a finite number of logarithms of "simple" functions.
A proof of Liouville's theorem can be found in section 12.4 of Geddes, et al.
Examples
As an example, the field C(x) of rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in a single variable has a derivation given by the standard derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with respect to that variable. The constants of this field are just the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C.
The function
, which exists in C(x), does not have an antiderivative in C(x). Its antiderivatives ln x + C do, however, exist in the logarithmic extension C(x, ln x).Likewise, the function
does not have an antiderivative in C(x). Its antiderivatives tan−1(x) + C do not seem to satisfy the requirements of the theorem, since they are not (apparently) sums of rational functions and logarithms of rational functions. However, a calculation with Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
shows that in fact the antiderivatives can be written in the required manner (as logarithms of rational functions).
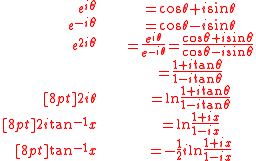
Relationship with differential Galois theory
Liouville's theorem is sometimes presented as a theorem in differential Galois theoryDifferential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
, but this is not strictly true. The theorem can be proved without any use of Galois theory. Furthermore, the Galois group of a simple antiderivative is either trivial (if no field extension is required to express it), or is simply the additive group of the constants (corresponding to the constant of integration). Thus, an antiderivative's differential Galois group does not encode enough information to determine if it can be expressed using elementary functions, the major condition of Liouville's theorem.