
Liouville's theorem (conformal mappings)
Encyclopedia
In mathematics
, Liouville's theorem, proved by Joseph Liouville
in 1850, is a rigidity theorem about conformal mappings in Euclidean space
. It states that any smooth
conformal mapping on a domain of Rn, where n > 2, can be expressed as a composition of translations
, similarities
, orthogonal transformations
and inversions: they are all Möbius transformations. This severely limits the variety of possible conformal mappings in R3 and higher-dimensional spaces. By contrast, conformal mappings in R2 can be much more complicated – for example, all simply connected planar domains are conformally equivalent, by the Riemann mapping theorem.
Generalizations of the theorem hold for transformations that are only weakly differentiable
. The focus of such a study is the non-linear Cauchy–Riemann system that is a necessary and sufficient condition for a smooth mapping ƒ → Ω → Rn to be conformal: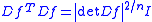
where Df is the Jacobian derivative, T is the matrix transpose, and I is the identity matrix. A weak solution of this system is defined to be an element ƒ of the Sobolev space
W(Ω,Rn) with non-negative Jacobian determinant almost everywhere
, such that the Cauchy–Riemann system holds at almost every point of Ω. Liouville's theorem is then that every weak solution (in this sense) is a Möbius transformation, meaning that it has the form
where a,b are vectors in Rn, α is a scalar, A is a rotation matrix, and ε = 0 or 2. Equivalently stated, any quasiconformal map of a domain in Euclidean space that is also conformal is a Möbius transformation. This equivalent statement justifies using the Sobolev space W1,n, since ƒ ∈ W(Ω,Rn) then follows from the geometrical condition of conformality and the ACL characterization of Sobolev space. The result is not optimal however: in even dimensions n = 2k, the theorem also holds for solutions that are only assumed to be in the space W, and this result is sharp in the sense that there are weak solutions of the Cauchy–Riemann system in W1,p for any p < k which are not Möbius transformations. In odd dimensions, it is known that W1,n is not optimal, but a sharp result is not known.
Similar rigidity results (in the smooth case) hold on any conformal manifold. The group of conformal isometries of an n-dimensional conformal Riemannian manifold
always has dimension that cannot exceed that of the full conformal group SO(n+1,1). Equality of the two dimensions holds exactly when the conformal manifold is isometric with the n-sphere or projective space
. Local versions of the result also hold: The Lie algebra
of conformal Killing fields in an open set has dimension less than or equal to that of the conformal group, with equality holding if and only if the open set is locally conformally flat.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Liouville's theorem, proved by Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
in 1850, is a rigidity theorem about conformal mappings in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It states that any smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
conformal mapping on a domain of Rn, where n > 2, can be expressed as a composition of translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, similarities
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
, orthogonal transformations
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and inversions: they are all Möbius transformations. This severely limits the variety of possible conformal mappings in R3 and higher-dimensional spaces. By contrast, conformal mappings in R2 can be much more complicated – for example, all simply connected planar domains are conformally equivalent, by the Riemann mapping theorem.
Generalizations of the theorem hold for transformations that are only weakly differentiable
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
. The focus of such a study is the non-linear Cauchy–Riemann system that is a necessary and sufficient condition for a smooth mapping ƒ → Ω → Rn to be conformal:
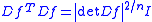
where Df is the Jacobian derivative, T is the matrix transpose, and I is the identity matrix. A weak solution of this system is defined to be an element ƒ of the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
W(Ω,Rn) with non-negative Jacobian determinant almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
, such that the Cauchy–Riemann system holds at almost every point of Ω. Liouville's theorem is then that every weak solution (in this sense) is a Möbius transformation, meaning that it has the form

where a,b are vectors in Rn, α is a scalar, A is a rotation matrix, and ε = 0 or 2. Equivalently stated, any quasiconformal map of a domain in Euclidean space that is also conformal is a Möbius transformation. This equivalent statement justifies using the Sobolev space W1,n, since ƒ ∈ W(Ω,Rn) then follows from the geometrical condition of conformality and the ACL characterization of Sobolev space. The result is not optimal however: in even dimensions n = 2k, the theorem also holds for solutions that are only assumed to be in the space W, and this result is sharp in the sense that there are weak solutions of the Cauchy–Riemann system in W1,p for any p < k which are not Möbius transformations. In odd dimensions, it is known that W1,n is not optimal, but a sharp result is not known.
Similar rigidity results (in the smooth case) hold on any conformal manifold. The group of conformal isometries of an n-dimensional conformal Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
always has dimension that cannot exceed that of the full conformal group SO(n+1,1). Equality of the two dimensions holds exactly when the conformal manifold is isometric with the n-sphere or projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
. Local versions of the result also hold: The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of conformal Killing fields in an open set has dimension less than or equal to that of the conformal group, with equality holding if and only if the open set is locally conformally flat.

