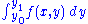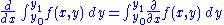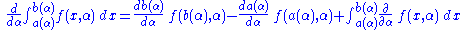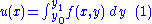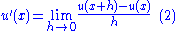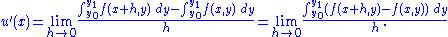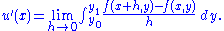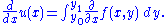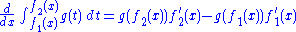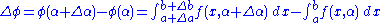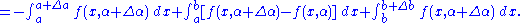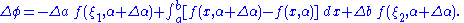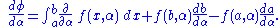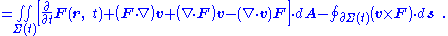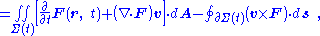
Leibniz integral rule
Encyclopedia
In mathematics
, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz
, tells us that if we have an integral
of the form
then for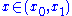 the derivative of this integral is thus expressible
the derivative of this integral is thus expressible
provided that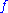 and
and 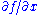 are both continuous over a region in the form
are both continuous over a region in the form
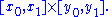
where the partial derivative of f indicates that inside the integral only the variation of ƒ ( x, α ) with α is considered in taking the derivative.
 A Leibniz integral rule for three dimensions is:
A Leibniz integral rule for three dimensions is:
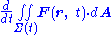
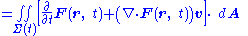
where:
So that, using difference quotient
s
Substitute equation (1) into equation (2), and combine the integrals (since the difference of two integrals equals the integral of the difference).
The term is constant, so can be included in the integrand.
term is constant, so can be included in the integrand.
Provided that the limit can be passed under the integral sign, we obtain
We claim that the passage of the limit under the integral sign is valid. Indeed, the bounded convergence theorem (a corollary of the dominated convergence theorem
) of real analysis states that if a sequence of functions on a set of finite measure is uniformly bounded and converges pointwise, then passage of the limit under the integral is valid. To complete the proof, we show that these hypotheses are satisfied by the family of difference quotients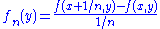 . Continuity of
. Continuity of 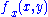 and compactness implies that
and compactness implies that 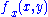 is uniformly bounded. Uniform boundedness of the difference quotients follows from uniform boundedness of
is uniformly bounded. Uniform boundedness of the difference quotients follows from uniform boundedness of 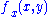 and the Mean Value Theorem
and the Mean Value Theorem
, since for all y and n, there exists z in the interval such that
such that 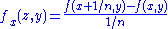 . The difference quotients converge pointwise to
. The difference quotients converge pointwise to 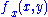 since
since 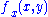 exists. This completes the proof.
exists. This completes the proof.
For a simpler proof using Fubini's theorem
, see the references.
 :
:
This follows from the chain rule
.
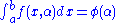 , where a and b are functions of α that exhibit increments Δa and Δb, respectively, when α is increased by Δα.
, where a and b are functions of α that exhibit increments Δa and Δb, respectively, when α is increased by Δα.
Then,
A form of the mean value theorem
,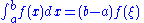 , where
, where 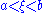 , may be applied to the first and last integrals of the formula for
, may be applied to the first and last integrals of the formula for 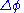 above, resulting in
above, resulting in
Dividing by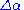 , and letting
, and letting  , and noticing
, and noticing  and
and  and using the result
and using the result
yields the general form of the Leibniz integral rule below:
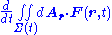

where the limits of integration confining the integral to the region Σ no longer are time dependent so differentiation passes through the integration to act on the integrand only:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, tells us that if we have an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the form
then for
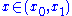 the derivative of this integral is thus expressible
the derivative of this integral is thus expressibleprovided that
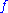 and
and 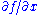 are both continuous over a region in the form
are both continuous over a region in the form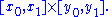
Variable limits
A more general result, applicable when the limits of integration a and b and the integrand ƒ( x, α ) all are functions of the parameter α is:where the partial derivative of f indicates that inside the integral only the variation of ƒ ( x, α ) with α is considered in taking the derivative.
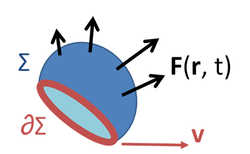
Three-dimensional, time-dependent case

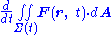
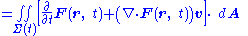
where:
-
- F ( r, t ) is a vector field at the spatial position r at time t
- Σ is a moving surface in three-space bounded by the closed curve ∂Σ
- d A is a vector element of the surface Σ
- d s is a vector element of the curve ∂Σ
- v is the velocity of movement of the region Σ
- ∇• is the vector divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
- × is the vector cross product
- The double integrals are surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
s over the surface Σ, and the line integralLine integralIn mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
is over the bounding curve ∂Σ.
Proof of basic form
Let:So that, using difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
s
Substitute equation (1) into equation (2), and combine the integrals (since the difference of two integrals equals the integral of the difference).
The
 term is constant, so can be included in the integrand.
term is constant, so can be included in the integrand.Provided that the limit can be passed under the integral sign, we obtain
-
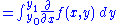 and therefore
and therefore
We claim that the passage of the limit under the integral sign is valid. Indeed, the bounded convergence theorem (a corollary of the dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
) of real analysis states that if a sequence of functions on a set of finite measure is uniformly bounded and converges pointwise, then passage of the limit under the integral is valid. To complete the proof, we show that these hypotheses are satisfied by the family of difference quotients
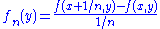 . Continuity of
. Continuity of 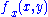 and compactness implies that
and compactness implies that 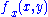 is uniformly bounded. Uniform boundedness of the difference quotients follows from uniform boundedness of
is uniformly bounded. Uniform boundedness of the difference quotients follows from uniform boundedness of 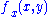 and the Mean Value Theorem
and the Mean Value TheoremMean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, since for all y and n, there exists z in the interval
 such that
such that 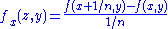 . The difference quotients converge pointwise to
. The difference quotients converge pointwise to 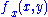 since
since 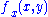 exists. This completes the proof.
exists. This completes the proof.For a simpler proof using Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
, see the references.
Variable limits form
For a monovariant function :
:This follows from the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
.
General form with variable limits
Now, suppose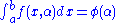 , where a and b are functions of α that exhibit increments Δa and Δb, respectively, when α is increased by Δα.
, where a and b are functions of α that exhibit increments Δa and Δb, respectively, when α is increased by Δα.Then,
A form of the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
,
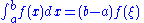 , where
, where 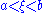 , may be applied to the first and last integrals of the formula for
, may be applied to the first and last integrals of the formula for 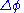 above, resulting in
above, resulting inDividing by
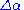 , and letting
, and letting  , and noticing
, and noticing  and
and  and using the result
and using the result
yields the general form of the Leibniz integral rule below:
Three-dimensional, time-dependent form
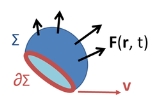
At time t the surface Σ in Figure 1 contains a set of points arranged about a centroid R ( t ) and function F ( r, t) can be written as F ( R ( t ) + r − R(t), t ) = F ( R ( t ) + ρ, t ), with ρ independent of time. Variables are shifted to a new frame of reference attached to the moving surface, with origin at R ( t ). For a rigidly translating surface, the limits of integration are then independent of time, so: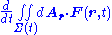

where the limits of integration confining the integral to the region Σ no longer are time dependent so differentiation passes through the integration to act on the integrand only:
-
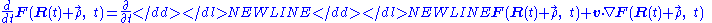
-
-
-
-
-
-

with the velocity of motion of the surface defined by: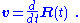
This equation expresses the material derivative of the field, that is, the derivative with respect to a coordinate system attached to the moving surface. Having found the derivative, variables can be switched back to the original frame of reference. We notice that (see article on curl ):
and that Stokes theorem allows the surface integral of the curl over Σ to be made a line integral over ∂Σ:
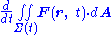
The sign of the line integral is based on the right-hand ruleRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
for the choice of direction of line element ds. To establish this sign, for example, suppose the field F points in the positive z-direction, and the surface Σ is a portion of the xy-plane with perimeter ∂Σ. We adopt the normal to Σ to be in the positive z-direction. Positive traversal of ∂Σ is then counterclockwise (right-hand rule with thumb along z-axis). Then the integral on the left-hand side determines a positive flux of F through Σ. Suppose Σ translates in the positive x-direction at velocity v. An element of the boundary of Σ parallel to the y-axis, say ds, sweeps out an area vt × ds in time t. If we integrate around the boundary ∂Σ in a counterclockwise sense, vt × ds points in the negative z-direction on the left side of ∂Σ (where ds points downward), and in the positive z-direction on the right side of ∂Σ (where ds points upward), which makes sense because Σ is moving to the right, adding area on the right and losing it on the left. On that basis, the flux of F is increasing on the right of ∂Σ and decreasing on the left. However, the dot-product v × F • ds = −F × v• ds = −F • v × ds. Consequently, the sign of the line integral is taken as negative.
If v is a constant,
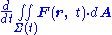
which is the quoted result. This proof does not consider the possibility of the surface deforming as it moves.
See also
- Chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
- Leibniz rule (generalized product rule)Leibniz rule (generalized product rule)In calculus, the general Leibniz rule, named after Gottfried Leibniz, generalizes the product rule. It states that if f and g are n-times differentiable functions, then the nth derivative of the product fg is given by...
- Differentiation under the integral sign
- Reynolds transport theoremReynolds transport theoremReynolds' transport theorem , or in short Reynolds theorem, is a three-dimensional generalization of the Leibniz integral rule which is also known as differentiation under the integral sign....
a generalization of Leibniz rule
-
-
-
-
-
-
-