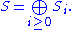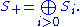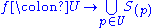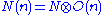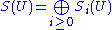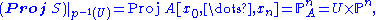Proj construction
Encyclopedia
In algebraic geometry
, Proj is a construction analogous to the spectrum-of-a-ring
construction of affine schemes, which produces objects with the typical properties of projective space
s and projective varieties. It is a fundamental tool in scheme theory.
In this article, all rings
will be assumed to be commutative and with identity.
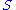be a graded ring where
We define the set Proj S to be the set of homogeneous prime ideal
s that do not contain the irrelevant ideal
For brevity we will sometimes use X for Proj S.
, called the Zariski topology
, on Proj S by defining the closed sets to be those of the form
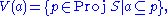
where a is a homogeneous ideal of S. As in the case of affine schemes it is quickly verified that the V(a) form the closed sets of a topology
on X.
Indeed if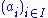
are a family of ideals, then we have
and if the indexing set I is finite, then
.
Equivalently, we may take the open sets as a starting point and define
A common shorthand is to denote D(Sf) by D(f), where Sf is the ideal
generated by f. For any a, D(a) and V(a) are obviously complementary and hence the same proof as before shows that the D(a) are a topology on Proj S. The advantage of this approach is that the D(f), where f ranges over all homogeneous elements of S, form a base
for this topology, which is an indispensable tool for the analysis of Proj S just as the analogous fact for the spectrum of a ring is likewise indispensable.
on Proj S, called the “structure sheaf” as in the affine case, which makes it into a scheme
. As in the case of the Spec construction there are many ways to proceed: the most direct one, which is also highly suggestive of the construction of regular functions on a projective variety in classical algebraic geometry, is the following. For any open set U of Proj S (which is by definition a set of homogeneous prime ideals of S not containing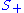
) we define the ring 
to be the set of all functions
(where
denotes the subring of the ring of fractions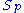 
consisting of fractions of homogeneous elements of the same degree) such that for each prime ideal p of U:
It follows immediately from the definition that the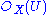
form a sheaf of rings 
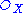on Proj S, and it may be shown that the pair (Proj S, 
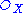) is in fact a scheme (this is accomplished by showing that each of the open subsets D(f) is in fact an affine scheme).
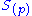for each prime ideal p of S. This property is also possessed by any graded module M over S, and therefore with the appropriate minor modifications the preceding section constructs for any such M a sheaf, denoted 
, of graded 
-modules on Proj S.
A special case of the sheaf associated to a graded module is when we take M to be S itself with a different grading: namely, we let the degree-d elements of M be the degree-(d + 1) elements of S, and denote M = S(1). We then obtain
as a sheaf of graded 
-modules on Proj S, denoted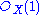 
or simply O(1), called the twisting sheaf of Serre (named after Jean-Pierre Serre
). It can be checked that O(1) is in fact an invertible sheaf
.
One reason for the utility of O(1) is that it recovers the algebraic information of S that was lost when, in the construction of
, we passed to fractions of degree zero. In the case Spec A for a ring A, the global sections of the structure sheaf form A itself, whereas the global sections of 
here form only the degree-zero elements of S. If we define
then each O(n) contains the degree-n information about S, and taken together they contain all the grading information that was lost. Likewise, for any sheaf of graded
-modules N we define
and expect this “twisted” sheaf to contain grading information about N. In particular, if N is the sheaf associated to a graded S-module M we likewise expect it to contain lost grading information about M. This suggests, though erroneously, that S can in fact be reconstructed from these sheaves; however, this is true in the case that S is a polynomial ring, below. This situation is to be contrasted with the fact that the spec functor is adjoint to the global sections functor in the category of locally ringed spaces.
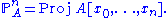
The grading on the polynomial ring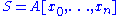
is defined by letting each 
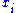have degree one and every element of A, degree zero. Comparing this to the definition of O(1), above, we see that the sections of O(1) are in fact linear homogeneous polynomials, generated by the 
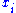themselves. This suggests another interpretation of O(1), namely as the sheaf of “coordinates” for Proj S, since the 
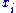are literally the coordinates for projective n-space.
and produces, as the end result, a scheme which might be thought of as a fibration of Proj's of rings. This construction is often used, for example, to construct projective space bundle
s over a base scheme
.
and S be a sheaf of graded
-algebras (the definition of which is similar to the definition of 
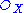-modules on a locally ringed space): that is, a sheaf with a direct sum decomposition
where each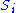
is an 
-module such that for every open subset U of X, S(U) is an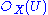 
-algebra and the resulting direct sum decomposition
is a grading of this algebra as a ring. Here we assume that
. We make the additional assumption that S is a quasi-coherent sheaf
; this is a “consistency” assumption on the sections over different open sets that is necessary for the construction to proceed.
U of X,
This definition suggests that we construct Proj S by first defining schemes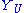
for each open affine U, by setting
and maps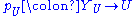
, and then showing that these data can be glued together “over” each intersection of two open affines U and V to form a scheme Y which we define to be Proj S. It is not hard to show that defining each 
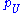to be the map corresponding to the inclusion of 
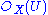into S(U) as the elements of degree zero yields the necessary consistency of the 
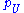, while the consistency of the 
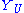themselves follows from the quasi-coherence assumption on S.
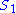is a coherent sheaf
and locally generates S over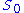
(that is, when we pass to the stalk
of the sheaf S at a point x of X, which is a graded algebra whose degree-zero elements form the ring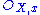
then the degree-one elements form a finitely-generated module over 
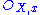and also generate the stalk as an algebra over it) then we may make a further construction. Over each open affine U, Proj S(U) bears an invertible sheaf
O(1), and the assumption we have just made ensures that these sheaves may be glued just like the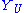
above; the resulting sheaf on Proj S is also denoted O(1) and serves much the same purpose for Proj S as the twisting sheaf on the Proj of a ring does.
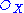-algebra, which means that there exists an open cover of X by open affines Spec A such that restricted to each of these, S is the sheaf associated with a polynomial ring over A. This is stronger than being simply quasi-coherent and implies, in particular, that the number of variables in each such ring is constant on connected components of X. By the construction above, we now have on a cover of X consisting of schemes U = Spec A
and hence Proj S is a projective space bundle.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Proj is a construction analogous to the spectrum-of-a-ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
construction of affine schemes, which produces objects with the typical properties of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s and projective varieties. It is a fundamental tool in scheme theory.
In this article, all rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
will be assumed to be commutative and with identity.
Proj as a set
Let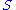 be a graded ring where
We define the set Proj S to be the set of homogeneous prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s that do not contain the irrelevant ideal
Irrelevant ideal
In mathematics, the irrelevant ideal is the ideal of a graded ring consisting of all homogeneous elements of degree greater than zero. More generally, a homogeneous ideal of a graded ring is called an irrelevant ideal if its radical contains the irrelevant ideal.The terminology arises from the...
For brevity we will sometimes use X for Proj S.
Proj as a topological space
We may define a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, called the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, on Proj S by defining the closed sets to be those of the form
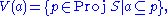
where a is a homogeneous ideal of S. As in the case of affine schemes it is quickly verified that the V(a) form the closed sets of a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on X.
Indeed if
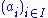are a family of ideals, then we have and if the indexing set I is finite, then.Equivalently, we may take the open sets as a starting point and define
A common shorthand is to denote D(Sf) by D(f), where Sf is the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by f. For any a, D(a) and V(a) are obviously complementary and hence the same proof as before shows that the D(a) are a topology on Proj S. The advantage of this approach is that the D(f), where f ranges over all homogeneous elements of S, form a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for this topology, which is an indispensable tool for the analysis of Proj S just as the analogous fact for the spectrum of a ring is likewise indispensable.
Proj as a scheme
We also construct a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on Proj S, called the “structure sheaf” as in the affine case, which makes it into a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. As in the case of the Spec construction there are many ways to proceed: the most direct one, which is also highly suggestive of the construction of regular functions on a projective variety in classical algebraic geometry, is the following. For any open set U of Proj S (which is by definition a set of homogeneous prime ideals of S not containing
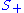) we define the ring to be the set of all functions
(where
denotes the subring of the ring of fractions 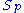consisting of fractions of homogeneous elements of the same degree) such that for each prime ideal p of U:- f(p) is an element of
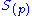; - There exists an open subset V of U containing p and homogeneous elements s, t of S of the same degree such that for each prime ideal q of V:
- t is not in q;
- f(q) = s/t.
It follows immediately from the definition that the
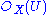form a sheaf of rings 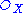on Proj S, and it may be shown that the pair (Proj S, 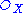) is in fact a scheme (this is accomplished by showing that each of the open subsets D(f) is in fact an affine scheme).The sheaf associated to a graded module
The essential property of S for the above construction was the ability to form localizations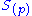 for each prime ideal p of S. This property is also possessed by any graded module M over S, and therefore with the appropriate minor modifications the preceding section constructs for any such M a sheaf, denoted , of graded -modules on Proj S.The twisting sheaf of Serre
- For related information, and the classical Serre twist sheaf, see tautological bundleTautological bundleIn mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
A special case of the sheaf associated to a graded module is when we take M to be S itself with a different grading: namely, we let the degree-d elements of M be the degree-(d + 1) elements of S, and denote M = S(1). We then obtain
as a sheaf of graded -modules on Proj S, denoted 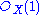or simply O(1), called the twisting sheaf of Serre (named after Jean-Pierre SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
). It can be checked that O(1) is in fact an invertible sheaf
Invertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
.
One reason for the utility of O(1) is that it recovers the algebraic information of S that was lost when, in the construction of
, we passed to fractions of degree zero. In the case Spec A for a ring A, the global sections of the structure sheaf form A itself, whereas the global sections of here form only the degree-zero elements of S. If we define
then each O(n) contains the degree-n information about S, and taken together they contain all the grading information that was lost. Likewise, for any sheaf of graded
-modules N we define
and expect this “twisted” sheaf to contain grading information about N. In particular, if N is the sheaf associated to a graded S-module M we likewise expect it to contain lost grading information about M. This suggests, though erroneously, that S can in fact be reconstructed from these sheaves; however, this is true in the case that S is a polynomial ring, below. This situation is to be contrasted with the fact that the spec functor is adjoint to the global sections functor in the category of locally ringed spaces.
Projective n-space
If A is a ring, we define projective n-space over A to be the schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
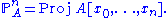
The grading on the polynomial ring
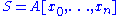is defined by letting each 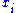have degree one and every element of A, degree zero. Comparing this to the definition of O(1), above, we see that the sections of O(1) are in fact linear homogeneous polynomials, generated by the 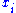themselves. This suggests another interpretation of O(1), namely as the sheaf of “coordinates” for Proj S, since the 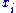are literally the coordinates for projective n-space.Global Proj
A generalization of the Proj construction replaces the ring S with a sheaf of algebrasSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
and produces, as the end result, a scheme which might be thought of as a fibration of Proj's of rings. This construction is often used, for example, to construct projective space bundle
Bundle
Bundle or Bundling may refer to:In marketing:* Product bundling, a marketing strategy that involves offering several products for sale as one combined product...
s over a base scheme
Grothendieck's relative point of view
Grothendieck's relative point of view is a heuristic applied in certain abstract mathematical situations, with a rough meaning of taking for consideration families of 'objects' explicitly depending on parameters, as the basic field of study, rather than a single such object...
.
Assumptions
Formally, let X be any schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and S be a sheaf of graded
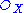-algebras (the definition of which is similar to the definition of -modules on a locally ringed space): that is, a sheaf with a direct sum decomposition
where each
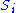is an -module such that for every open subset U of X, S(U) is an 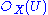-algebra and the resulting direct sum decomposition
is a grading of this algebra as a ring. Here we assume that
. We make the additional assumption that S is a quasi-coherent sheafCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
; this is a “consistency” assumption on the sections over different open sets that is necessary for the construction to proceed.
Construction
In this setup we may construct a scheme Proj S and a “projection” map p onto X such that for every open affineScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
U of X,
This definition suggests that we construct Proj S by first defining schemes
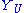for each open affine U, by setting
and maps
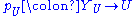, and then showing that these data can be glued together “over” each intersection of two open affines U and V to form a scheme Y which we define to be Proj S. It is not hard to show that defining each 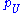to be the map corresponding to the inclusion of 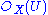into S(U) as the elements of degree zero yields the necessary consistency of the 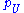, while the consistency of the 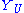themselves follows from the quasi-coherence assumption on S.The twisting sheaf
If S has the additional property that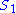 is a coherent sheafCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
and locally generates S over
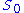(that is, when we pass to the stalkSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of the sheaf S at a point x of X, which is a graded algebra whose degree-zero elements form the ring
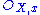then the degree-one elements form a finitely-generated module over 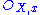and also generate the stalk as an algebra over it) then we may make a further construction. Over each open affine U, Proj S(U) bears an invertible sheafInvertible sheaf
In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...
O(1), and the assumption we have just made ensures that these sheaves may be glued just like the
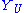above; the resulting sheaf on Proj S is also denoted O(1) and serves much the same purpose for Proj S as the twisting sheaf on the Proj of a ring does.Projective space bundles
As mentioned above, we obtain projective space bundles as a special case of this construction. To do this, we take S to be locally free as an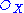-algebra, which means that there exists an open cover of X by open affines Spec A such that restricted to each of these, S is the sheaf associated with a polynomial ring over A. This is stronger than being simply quasi-coherent and implies, in particular, that the number of variables in each such ring is constant on connected components of X. By the construction above, we now have on a cover of X consisting of schemes U = Spec A
and hence Proj S is a projective space bundle.