Kakeya needle problem
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kakeya set, or Besicovitch set, is any set of points in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
which contains a unit line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
in every direction. While many types of objects satisfy this property, several interesting results and questions are motivated by considering how small such sets can be. Besicovitch
Abram Samoilovitch Besicovitch
Abram Samoilovitch Besicovitch was a Russian mathematician, who worked mainly in England. He was born in Berdyansk on the Sea of Azov to a Karaite family.-Life and career:...
showed that there are Besicovitch sets of measure zero.
A Kakeya needle set (sometimes also known as a Kakeya set) is a (Besicovitch) set within which a unit line segment can be rotated continuously through 180 degrees, returning to its original position with reversed orientation. Besicovitch showed that there are Kakeya needle sets of arbitrarily small positive measure.
Kakeya needle problem
The Kakeya needle problem asks whether there is a minimum area of a region D in the plane, in which a needle can be turned through 360°. This question was first posed, for convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
regions, by .
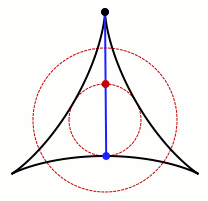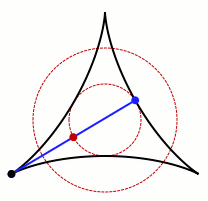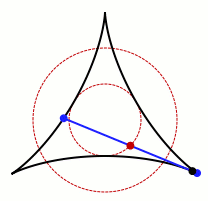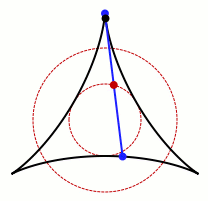
He seems to have suggested that D of minimum area, without the convexity restriction, would be a three-pointed deltoid
Deltoid curve
In geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
shape. The original problem was solved by Pál
Gyula Pál
Gyula Pál was a noted Hungarian-Danish mathematician. He is known for his work on Jordan curves both in plane and space, and on the Kakeya problem...
.
The early history of this question has been subject to some discussion, though.
Besicovitch sets
Abram Samoilovitch Besicovitch
Abram Samoilovitch Besicovitch was a Russian mathematician, who worked mainly in England. He was born in Berdyansk on the Sea of Azov to a Karaite family.-Life and career:...
was able to show that there is no lower bound > 0 for the area of such a region D, in which a needle of unit length can be turned round. This built on earlier work of his, on plane sets which contain a unit segment in each orientation. Such a set is now called a Besicovitch set. Besicovitch's work showing such a set could have arbitrarily small measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
was from 1919. The problem may have been considered by analysts before that.
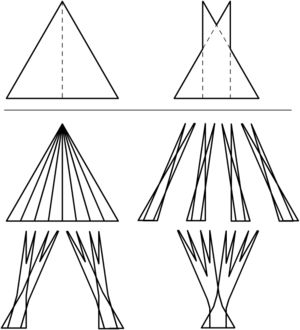
One method of constructing a Besicovitch set can be described as follows (see figure for corresponding illustrations). The following is known as a "Perron tree" after O. Perron who was able to simplify Besicovitch's original construction: take a triangle with height 1, divide it in two, and translate both pieces over each other so that their bases overlap on some small interval. Then this new figure will have a reduced total area.
Now, suppose we divide our triangle into eight subtriangles. For each consecutive pair of triangles, perform the same overlapping operation we described before to get four new shapes, each consisting of two overlapping triangles. Next, overlap consecutive pairs of these new shapes by shifting their bases over each other partially, so we're left with two shapes, and finally overlap these two in the same way. In the end, we get a shape looking somewhat like a tree, but with an area much smaller than our original triangle.
To construct an even smaller set, subdivide your triangle into, say,
triangles each of base length 
, and perform the same operations as we did before when we divided our triangle twice and eight times. If the amount of overlap we do on each triangle is small enough and the size 
of the subdivision of our triangle is large enough, we can form a tree of area as small as we like. A Besicovitch set can be created by combining three rotations of a Perron tree created from an equilateral triangle.Adapting this method further, we can construct a sequence of sets whose intersection is a Besicovitch set of measure zero. One way of doing this is to observe that if we have any parallelogram two of whose sides are on the lines x=0 and x = 1 then we can find a union of parallelograms also with sides on these lines, whose total area is arbitrarily small and which contain translates of all lines joining a point on
x=0 to a point on x = 1 that are in the original parallelogram. This follows from a slight variation of Besicovich's construction above. By repeating this we can find a sequence of sets
each a finite union of parallelograms between the lines x=0 and x = 1, whose areas tend to zero and each of which contains translates of all lines joining x=0 and x = 1 in a unit square. The intersection of these sets is then a measure 0 set containing translates of all these lines, so a union of two copies of this intersection is a measure 0 Besicovich set.
There are other methods for constructing Besicovitch sets of measure zero aside from the 'sprouting' method. For example, Kahane
Jean-Pierre Kahane
Jean-Pierre Kahane is a French mathematician.Kahane attended the École normale supérieure and obtained the agrégation of mathematics in 1949. He then worked for the CNRS from 1949 to 1954, first as an intern and then as a research assistant...
uses Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
s to construct a Besicovitch set of measure zero in the two-dimensional plane.
Kakeya needle sets
By using a trick of Pál, known as Pál joins (given two parallel lines, any unit line segmentcan be moved continuously from one to the other on a set of arbitrary small measure), a set in which a unit line segment can be rotated continuously through 180 degrees can be created from a Besicovitch set consisting of Perron trees.
In 1941, H. J. Van Alphen showed that there are arbitrary small Kakeya needle sets inside a circle with radius
(arbitrary 
).Simply connected Kakeya needle sets with smaller area than the deltoid were
found in 1965. Melvin Bloom and I. J. Schoenberg independently presented Kakeya needle sets with areas approaching to
, the Bloom-Schoenberg number. Schoenberg conjectured that this numberis the lower bound for the area of simply connected Kakeya needle sets.
However, in 1971, F. Cunningham showed that, given
, there is a simply connected Kakeya needle set of area less than
contained in a circle of radius 1.Although there are Kakeya needle sets of arbitrarily small positive measure and Besicovich sets of measure 0, there are no Kakaya needle sets of measure 0.
Statement
The same question of how small these Besicovitch sets could be was then posed in higher dimensions, giving rise to a number of conjectures known collectively as the Kakeya conjectures, and have helped initiate the field of mathematics known as geometric measure theoryGeometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
. In particular, if there exist Besicovitch sets of measure zero, could they also have s-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
zero for some dimension s less than the dimension of the space in which they lie? This question gives rise to the following conjecture:
-
- Kakeya set conjecture: Define a Besicovitch set in Rn to be a set which contains a unit line segment in every direction. Is it true that such sets necessarily have Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
and Minkowski dimension equal to n?
- Kakeya set conjecture: Define a Besicovitch set in Rn to be a set which contains a unit line segment in every direction. Is it true that such sets necessarily have Hausdorff dimension
This is known to be true for n = 1, 2 but only partial results are known in higher dimensions.
Kakeya maximal function
A modern way of approaching this problem is to consider a particular type of maximal functionMaximal function
Maximal functions appear in many forms in harmonic analysis . One of the most important of these is the Hardy–Littlewood maximal function. They play an important role in understanding, for example, the differentiability properties of functions, singular integrals and partial differential equations...
, which we construct as follows: Denote Sn-1 ⊂ Rn to be the unit sphere in n-dimensional space. Define
to be the cylinder of length 1, radius 
, centered at the point a ∈ Rn, and whose long side is parallel to the direction of the unit vector e ∈ Sn-1. Then for a locally integrable function f, we define the Kakeya maximal function of f to be
where m denotes the n-dimensional Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. Notice that
is defined for vectors e in the sphere Sn-1.Then there is a conjecture for these functions that, if true, will imply the Kakeya set conjecture for higher dimensions:
-
- Kakeya maximal function conjecture: For all
, there exists a constant 
such that for any function f and all 
,
- Kakeya maximal function conjecture: For all
-
- (see lp spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for notation).
- (see lp space
Results
Some results toward proving the Kakeya conjecture are the following:- The Kakeya conjecture is true for n = 1 (trivially) and n = 2 (Davies).
- In any n-dimensional space, Wolff showed that the dimension of a Kakeya set must be at least
(n+2).
- In 2002, Katz and Tao improved Wolff's bound to
, which is better for n>4.
- In 2000 Jean BourgainJean BourgainJean Bourgain is a Belgian mathematician. He has been a faculty member at the University of Illinois, Urbana-Champaign and, from 1985 until 1995, professor at Institut des Hautes Études Scientifiques at Bures-sur-Yvette in France, and since 1994 at the Institute for Advanced Study in Princeton,...
connected the Kakeya problem to arithmetic combinatoricsArithmetic combinatoricsArithmetic combinatorics arose out of the interplay between number theory, combinatorics, ergodic theory and harmonic analysis. It is about combinatorial estimates associated with arithmetic operations...
which involves harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and additive number theoryAdditive number theoryIn number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
.
Applications to analysis
Somewhat surprisingly, these conjectures have been shown to be connected to a number of questions in other fields, notably in harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. For instance, in 1971, Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
was able to use the Besicovitch set construction to show that in dimensions greater than 1, truncated Fourier integrals taken over balls centered at the origin with radii tending to infinity need not converge in Lp norm
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
when p ≠ 2 (this is in contrast to the one-dimensional case where such truncated integrals do converge).
Sets containing circles and spheres
Analogues of the Kakeya problem include considering sets containing more general shapes than lines, such as circles.- In 1997 and 1999, Wolff proved that sets containing a sphere of every radius must have full dimension, that is, the dimension is equal to the dimension of the space it is lying in, and proved this by proving bounds on a circular maximal function analogous to the Kakeya maximal function.
- It was conjectured that there existed sets containing a sphere around every point of measure zero. Results of Elias Stein proved all such sets must have positive measure when
, and Marstrand proved the same for the case n=2.
Sets containing k-dimensional disks
A generalization of the Kakeya conjecture is to consider sets that contain, instead of segments of lines in every direction, but, say, portions of k-dimensional subspaces. Define an (n,k) -Besicovitch set K to be a compact set in Rn containing a translate of every k-dimensional unit disk which has Lebesgue measure zero. That is, if B denotes the unit ball centered at zero, for every k-dimensional subspace P, there exists x ∈ Rn such that
. Hence, a (n,1)-Besicovitch set is the standard Besicovitch set described earlier.-
- The (n,k)-Besicovitch conjecture: There are no (n,k)-Besicovitch sets for k>1.
In 1979, Marstrand proved that there were no (3,2)-Besicovitch sets. At around the same time, however, Falconer proved that there were no (n,k)-Besicovitch sets for 2k>n. The best bound to date is by Bourgain, who proved in that no such sets exist when 2k-1+k>n.
Kakeya sets in vector spaces over finite fields
In 1999, Wolff posed the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
analogue to the Kakeya problem, in hopes that the techniques for solving this conjecture could be carried over to the Euclidean case.
-
- Finite Field Kakeya Conjecture: Let F be a finite field, let K ⊆ Fn be a Kakeya set, i.e. for each vector y ∈ Fn there exists x ∈ Fn such that K contains a line {x+ty: t ∈ F} . Then the set K has size at least cn|F|n where cn>0 is a constant that only depends on n.
Zeev proved this conjecture for cn = 1/n!, using what Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
called a "beautifully simple argument", as follows. Dvir observed that any polynomial in n variables of degree less than |F| vanishing on a Kakeya set must be identically zero. On the other hand, the polynomials in n variables of degree less than |F| form a vector space of dimension
Therefore there is at least one non-trivial polynomial of degree less than |F| that vanishes on any given set with less than this number of points. Combining these two observations shows that Kayeka sets must have at least |F|n/n! points. It is not clear whether the techniques will extend to proving the original Kakeya conjecture but this proof does lend credence to the original conjecture by making essentially algebraic counterexamples unlikely. Dvir has written a survey article on recent (as of 2009) progress on the finite field Kakeya problem and its relationship to randomness extractor
Randomness extractor
A randomness extractor, often simply called "an extractor," is a function which, when applied to a high-entropy source , generates a random output that is shorter, but uniformly distributed...
s.