
Homothetic center
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a homothetic center (also called a center of similarity or a center of similitude) is a point from which at least two geometrically similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
figures can be seen as a dilation/contraction
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense. If the center is internal, the two figures are scaled mirror images of one another; their angles have the opposite sense.

General polygons
If two geometric figures possess a homothetic center, they are similarSimilarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to one another; in other words, they must have the same angles at corresponding points and differ only in their relative scaling. The homothetic center and the two figures need not lie in the same plane; they can be related by a projection
3D projection
3D projection is any method of mapping three-dimensional points to a two-dimensional plane. As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting.-...
from the homothetic center.
Homothetic centers may be external or internal. If the center is internal, the two geometric figures are scaled mirror images of one another; in technical language, they have opposite chirality
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
. A clockwise angle in one figure would correspond to a counterclockwise angle in the other. Conversely, if the center is external, the two figures are directly similar to one another; their angles have the same sense.
Circles
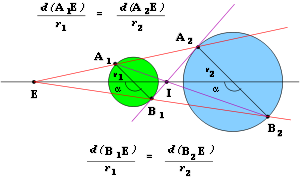
For a given pair of circles, the internal and external homothetic centers may be found as follows. Two radii are drawn in the two circles such that they make the same angle with the line joining their centers (the angle α in Figure 3). A line drawn through corresponding endpoints of those radii (e.g., the points A1 and A2 in Figure 3) intersects the line of centers at the external homothetic center. Conversely, a line drawn through one endpoint and the diametric opposite endpoint of its counterpart (e.g., the points A1 and B2 in Figure 3) intersects the line of centers at the internal homothetic center.
As a limiting case of this construction, a line tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to both circles, where the circles fall on opposite sides, passes through the internal homothetic center, as illustrated by the line joining the points B1 and A2 in Figure 3. Conversely, a line tangent to both given circle, where the circles fall on the same side, passes through the external homothetic center. See also Tangent lines to circles
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
.
Homologous and antihomologous points
In general, a ray emanating from a homothetic center will intersect each of its circles in two places. Of these four points, two are said to be homologous if radii drawn to them make the same angle with the line connecting the centers, e.g., the points A1 and A2 in Figure 3. Points which are collinear with respect to the homothetic center but are not homologous are said to be antihomologous, e.g., points Q and P′ in Figure 4.Pairs of antihomologous points lie on a circle
When two rays from the same homothetic center intersect the circles, each set of antihomologous points lie on a circle.Let's consider triangles EQS and EQ′S′ (Figure 4).
They are similar because both share angle ∠QES=∠Q′ES′ and

since E is the homothetic center.
From that similarity follows that ∠ESQ=∠ES′Q′=α.
Because of the inscribed angle theorem ∠EP′R′=∠ES′Q′.
∠QSR′=180°-α since it is supplementary
Supplementary angles
Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
to ∠ESQ.
In the quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
QSR′P′ ∠QSR′+∠QP′R′=180°-α+α=180° which means it can be inscribed in a circle
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
.
From the secant theorem follows that EQ·EP′=ES·ER′.
In the same way it can be shown that PRS′Q′ can be inscribed in circle and EP·EQ′=ER·ES′.
The proof is similar for the internal homothetic center I.
PIR~P′IR′ then ∠RPI=∠IP′R′=α.
∠RS′Q′=∠PP′R′=α (inscribed angle theorem).
Segment RQ′ is seen in the same angle from P and S′ which means R, P, S′ and Q′ lie on a circle.
Then from intersecting chords theorem IP·IQ′=IR·IS′.
Similarly QSP′R′ can be inscribed in a circle and IQ·IP′=IS·IR′.
Relation with the radical axis
Two circles have a radical axisRadical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
, which is the line of points from which tangents to both circles have equal length. More generally, every point on the radical axis has the property that its powers
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
relative to the circles are equal. The radical axis is always perpendicular to the line of centers, and if two circles intersect, their radical axis is the line joining their points of intersection. For three circles, three radical axes can be defined, one for each pair of circles (C1/C2, C1/C3, and C2/C3); remarkably, these three radical axes intersect at a single point, the radical center. Tangents drawn from the radical center to the three circles would all have equal length.
Any two pairs of antihomologous points can be used to find a point on the radical axis. Consider the two rays emanating from the external homothetic center E in Figure 4. These rays intersect the two given circles (green and blue in Figure 4) in two pairs of antihomologous points, Q and P′ for the first ray, and S and R′ for the second ray. These four points lie on a single circle, that intersects both given circles. By definition, the line QS is the radical axis of the new circle with the green given circle, whereas the line P′R′ is the radical axis of the new circle with the blue given circle. These two lines intersect at the point G, which is the radical center of the new circle and the two given circles. Therefore, the point G also lies on the radical axis of the two given circles.
Tangent circles and antihomologous points
For each pair of antihomologous points of two circles exists a third circle which is tangent to the given ones and touches them at the antihomologous points.The opposite is also true — every circle which is tangent to two other circles touches them at a pair of antihomologous points.
Let our two circles have centers O1 and O2 (Figure 5). E is their external homothetic center.
We construct an arbitrary ray from E which intersects the two circles in P, Q, P′ and Q′.
Extend O1Q and O2P′ until they intersect in T1.
It is easily proven that triangles O1PQ and O2P′Q′ are similar because of the homothety. They are also isosceles because O1P=O1Q (radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
), therefore
∠O1PQ=∠O1QP=∠O2P′Q′=∠O2Q′P′=∠T1QP′=∠T1P′Q.
Thus T1P′Q is also isosceles and a circle can be constructed with center T1 and radius T1P′=T1Q. This circle is tangent to the two given circles in points Q and P′.
The proof for the other pair of antihomologous points (P and Q′), as well as in the case of the internal homothetic center is analogous.
If we construct the tangent circles for every possible pair of antihomologous points we get two families of circles - one for each homothetic center. The family of circles of the external homothetic center is such that every tangent circle either contains both given circles or none (Figure 6). On the other hand the circles from the other family always contain only one of the given circles (Figure 7).
All circles from a tangent family have a common radical center and it coincides with the homothetic center.
To show this let's consider two rays from the homothetic center, intersecting the given circles (Figure 8). Two tangent circles T1 and T2 exist which touch the given circles at the antihomologous points. As we've already shown these points lie on a circle C and thus the two rays are radical axes for C/T1 and C/T2. Then the intersecting point of the two radical axes must also belong to the radical axis of T1/T2. This point of intersection is the homothetic center E.
If the two tangent circle touch collinear pairs of antihomologous point — as in Figure 5 — then because of the homothety
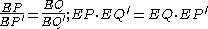 . Thus the powers of E with respect to the two tangent circles are equal which means that E belongs to the radical axis.
. Thus the powers of E with respect to the two tangent circles are equal which means that E belongs to the radical axis.Homothetic centers of three circles
Any pair of circles has two centers of similarity, therefore, three circles would have six centers of similarity, two for each distinct pair of given circles. Remarkably, these six points lie on four lines, three points on each line. Here is one way to show this.Consider the plane of the three circles (Figure 9). Offset each center point perpendicularly to the plane by a distance equal to the corresponding radius. The centers can be offset to either side of the plane. The three offset points define a single plane. In that plane we build three lines through each pair of points. The lines pierce the plane of circles in the points HAB, HBC and HAC. Since the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of points which are common to two distinct and non-parallel planes is a line then necessarily these three points lie on such line. From the similarity of triangles HABAA′ and HABBB′ we see that
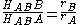 (rA,B being the radii of the circles) and thus HAB is in fact the homothetic center of the corresponding two circles. We can do the same for HBC and HAC.
(rA,B being the radii of the circles) and thus HAB is in fact the homothetic center of the corresponding two circles. We can do the same for HBC and HAC.Repeating the above procedure for different combinations of homothetic centers (in our method this is determined by the side to which we offset the centers of the circles) would yield a total of four lines — three homothetic centers on each line (Figure 10).
Here is yet another way to prove this.
Let C1 and C2 be a conjugate pair of circles tangent to all three given circles (Figure 11). By conjugate we imply that both tangent circles belong to the same family with respect to any one of the given pairs of circles. As we've already seen, the radical axis of any two tangent circles from the same family passes through the homothetic center of the two given circles. Since the tangent circles are common for all three pairs of given circles then their homothetic centers all belong to the radical axis of C1 and C2 e.g., they lie on a single line.
This property is exploited in Joseph Diaz Gergonne's
Joseph Diaz Gergonne
Joseph Diaz Gergonne was a French mathematician and logician.-Life:In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion because the French government feared a foreign invasion intended to undo the French Revolution and restore Louis XVI to full power...
general solution to Apollonius' problem
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
. Given the three circles, the homothetic centers can be found and thus the radical axis of a pair of solution circles. Of course, there are infinitely many circles with the same radical axis, so additional work is done to find out exactly which two circles are the solution.
See also
- Similarity (geometry)Similarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
- Homothetic transformation
- Radical axisRadical axisThe radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
, radical center - Apollonius' problem

