Haefliger structure
Encyclopedia
In mathematics, a Haefliger structure on a topological space
is a generalization of a foliation
of a manifold, introduced by . Any foliation on a manifold induces a Haefliger structure, which uniquely determines the foliation.
Uα ∩ Uβ to the sheaf of germ
s of local diffeomorphisms of Rq, satisfying the 1-cocycle condition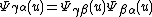
for 
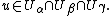
More generally, Cr, PL, analytic, and continuous Haefliger structures are defined by replacing sheaves of germs of smooth diffeomorphisms by the appropriate sheaves.
φα from each open set Uα to Rq, such that
for each α, β there is a map Φαβ from
Uα ∩ Uβ to local diffeomorphisms with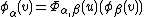
whenever v is close enough to u. The Haefliger cocycle is defined by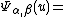
germ of 
at u.
An advantage of Haefliger structures over foliations is that they are closed under pullbacks. If f is a continuous map from X to Y then one can take pullbacks of foliations on Y provided that f is transverse to the foliation, but if f is not transverse the pullback can be a Haefliger structure that is not a foliation.
X×[0,1] to X×0 and X×1.
If f is a continuous map from X to Y, then there is a pullback under f of Haefliger structures on Y to Haefliger structures on X.
There is a classifying space BΓq for codimension-q Haefliger structures which has a universal Haefliger structure on it in the following sense. For any topological space X and continuous map from X to BΓq the pullback of the universal Haefliger structure is a Haefliger structure on X. For well-behaved
topological spaces X this induces a 1:1 correspondence between homotopy classes of maps
from X to BΓq and concordance classes of Haefliger structures.
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a generalization of a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of a manifold, introduced by . Any foliation on a manifold induces a Haefliger structure, which uniquely determines the foliation.
Definition
A Haefliger structure on a space X is determined by a Haefliger cocycle. A codimension-q Haefliger cocycle consists of a covering of X by open sets Uα, together with continuous maps Ψαβ fromUα ∩ Uβ to the sheaf of germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
s of local diffeomorphisms of Rq, satisfying the 1-cocycle condition
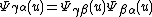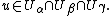
for More generally, Cr, PL, analytic, and continuous Haefliger structures are defined by replacing sheaves of germs of smooth diffeomorphisms by the appropriate sheaves.
Haefliger structure and foliations
A codimension-q foliation can be specified by a covering of X by open sets Uα, together with a submersionSubmersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
φα from each open set Uα to Rq, such that
for each α, β there is a map Φαβ from
Uα ∩ Uβ to local diffeomorphisms with
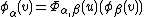
whenever v is close enough to u. The Haefliger cocycle is defined by
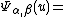germ of at u.An advantage of Haefliger structures over foliations is that they are closed under pullbacks. If f is a continuous map from X to Y then one can take pullbacks of foliations on Y provided that f is transverse to the foliation, but if f is not transverse the pullback can be a Haefliger structure that is not a foliation.
Classifying space
Two Haefliger structures on X are called concordant if they are the restrictions of Haefliger structures onX×[0,1] to X×0 and X×1.
If f is a continuous map from X to Y, then there is a pullback under f of Haefliger structures on Y to Haefliger structures on X.
There is a classifying space BΓq for codimension-q Haefliger structures which has a universal Haefliger structure on it in the following sense. For any topological space X and continuous map from X to BΓq the pullback of the universal Haefliger structure is a Haefliger structure on X. For well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
topological spaces X this induces a 1:1 correspondence between homotopy classes of maps
from X to BΓq and concordance classes of Haefliger structures.