
Grzegorczyk hierarchy
Encyclopedia
The Grzegorczyk hierarchy , named after the Polish logician Andrzej Grzegorczyk
, is a hierarchy of functions used in computability theory
(Wagner and Wechsung 1986:43). Every function
in the Grzegorczyk hierarchy is a primitive recursive function
, and every primitive recursive function appears in the hierarchy at some level. The hierarchy deals with the rate at which the values of the functions grow; intuitively, functions in lower level of the hierarchy grow slower than functions in the higher levels.
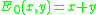 and
and 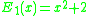 . I.e., E0 is the addition function, and E1 is a unary function which squares its argument and adds two. Then, for each n greater than 1, we define
. I.e., E0 is the addition function, and E1 is a unary function which squares its argument and adds two. Then, for each n greater than 1, we define 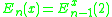 .
.
From these functions we define the Grzegorczyk hierarchy. , the n-th set in the hierarchy, contains the following functions:
, the n-th set in the hierarchy, contains the following functions:
In other words, is the closure
is the closure
of set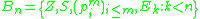 with respect to function composition and limited recursion (as defined above).
with respect to function composition and limited recursion (as defined above).
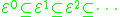
because they are closures over the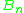 's and
's and 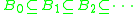 .
.
They are strict subsets (Rose 1984; Gakwaya 1997). In other words
because the hyper operation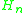 is in
is in 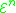 but not in
but not in  .
.
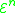 is the same as that of the primitive recursive function
is the same as that of the primitive recursive function
s, RP, except that recursion is limited (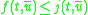 for some j in
for some j in 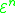 ) and the functions
) and the functions  are explicitly included in
are explicitly included in 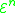 . Thus the Grzegorczyk hierarchy can be seen as a way to limit the power of primitive recursion to different levels.
. Thus the Grzegorczyk hierarchy can be seen as a way to limit the power of primitive recursion to different levels.
It is clear from this fact that all functions in any level of the Grzegorczyk hierarchy are primitive recursive functions (i.e.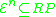 ) and thus:
) and thus: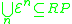
It can also be shown that all primitive recursive functions are in some level of the hierarchy (Rose 1984; Gakwaya 1997), thus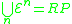
and the sets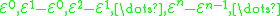 partition
partition
the set of primitive recursive functions, RP.
s. Such extensions define a fast-growing hierarchy
. To do this, the generating functions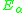 must be recursively defined for limit ordinals (note they have already been recursively defined for successor ordinals by the relation
must be recursively defined for limit ordinals (note they have already been recursively defined for successor ordinals by the relation 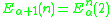 ). If there is a standard way of defining a fundamental sequence
). If there is a standard way of defining a fundamental sequence 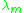 , whose limit ordinal is
, whose limit ordinal is 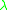 , then the generating functions can be defined
, then the generating functions can be defined 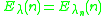 . However, this definition depends upon a standard way of defining the fundamental sequence. Rose (1984) suggests a standard way for all ordinals α < ε0.
. However, this definition depends upon a standard way of defining the fundamental sequence. Rose (1984) suggests a standard way for all ordinals α < ε0.
The original extension was due to Martin Löb
and Stan S. Wainer (1970) and is sometimes called the Löb–Wainer hierarchy.
Andrzej Grzegorczyk
Andrzej Grzegorczyk is a Polish mathematician. He is known for his work in computability, logic, and the foundations of mathematics...
, is a hierarchy of functions used in computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
(Wagner and Wechsung 1986:43). Every function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
in the Grzegorczyk hierarchy is a primitive recursive function
Primitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
, and every primitive recursive function appears in the hierarchy at some level. The hierarchy deals with the rate at which the values of the functions grow; intuitively, functions in lower level of the hierarchy grow slower than functions in the higher levels.
Definition
First we introduce an infinite set of functions, denoted Ei for some natural number i. We define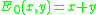 and
and 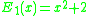 . I.e., E0 is the addition function, and E1 is a unary function which squares its argument and adds two. Then, for each n greater than 1, we define
. I.e., E0 is the addition function, and E1 is a unary function which squares its argument and adds two. Then, for each n greater than 1, we define 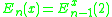 .
.From these functions we define the Grzegorczyk hierarchy.
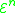 , the n-th set in the hierarchy, contains the following functions:
, the n-th set in the hierarchy, contains the following functions:
- Ek for k < n
- the zero function (Z(x) = 0);
- the successor function (S(x) = x + 1);
- the projection functions (
 );
); - the (generalized) compositions of functionsFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
in the set (if h, g1, g2, ... and gm are in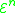 , then
, then 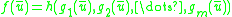 is as well); and
is as well); and - the results of limited (primitive) recursion applied to functions in the set, (if g, h and j are in
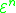 and
and 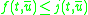 for all t and
for all t and 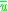 , and further
, and further 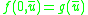 and
and 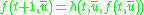 , then f is in
, then f is in  as well)
as well)
In other words,
 is the closure
is the closureClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of set
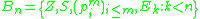 with respect to function composition and limited recursion (as defined above).
with respect to function composition and limited recursion (as defined above).Properties
These sets clearly form the hierarchy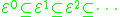
because they are closures over the
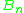 's and
's and 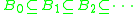 .
.They are strict subsets (Rose 1984; Gakwaya 1997). In other words

because the hyper operation
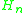 is in
is in 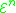 but not in
but not in  .
.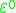 includes functions such as x+1, x+2, ...
includes functions such as x+1, x+2, ...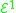 provides all addition functions, such as x+y, 4x, ...
provides all addition functions, such as x+y, 4x, ... provides all multiplication functions, such as xy, x4
provides all multiplication functions, such as xy, x4 provides all exponentiation functions, such as xy, 222x, and is exactly the elementary recursive functions.
provides all exponentiation functions, such as xy, 222x, and is exactly the elementary recursive functions.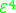 provides all tetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
provides all tetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
functions, and so on.
Relation to primitive recursive functions
The definition of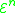 is the same as that of the primitive recursive function
is the same as that of the primitive recursive functionPrimitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
s, RP, except that recursion is limited (
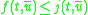 for some j in
for some j in 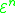 ) and the functions
) and the functions  are explicitly included in
are explicitly included in 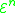 . Thus the Grzegorczyk hierarchy can be seen as a way to limit the power of primitive recursion to different levels.
. Thus the Grzegorczyk hierarchy can be seen as a way to limit the power of primitive recursion to different levels.It is clear from this fact that all functions in any level of the Grzegorczyk hierarchy are primitive recursive functions (i.e.
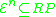 ) and thus:
) and thus: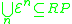
It can also be shown that all primitive recursive functions are in some level of the hierarchy (Rose 1984; Gakwaya 1997), thus
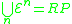
and the sets
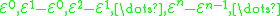 partition
partitionPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
the set of primitive recursive functions, RP.
Extensions
The Grzegorczyk hierarchy can be extended to transfinite ordinalOrdinal
Ordinal may refer to:* Ordinal number , a word representing the rank of a number* Ordinal scale, ranking things that are not necessarily numbers* Ordinal indicator, the sign adjacent to a numeral denoting that it is an ordinal number...
s. Such extensions define a fast-growing hierarchy
Fast-growing hierarchy
In computability theory, computational complexity theory and proof theory, a fast-growing hierarchy is an ordinal-indexed family of rapidly increasing functions fα: N → N...
. To do this, the generating functions
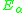 must be recursively defined for limit ordinals (note they have already been recursively defined for successor ordinals by the relation
must be recursively defined for limit ordinals (note they have already been recursively defined for successor ordinals by the relation 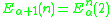 ). If there is a standard way of defining a fundamental sequence
). If there is a standard way of defining a fundamental sequence 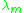 , whose limit ordinal is
, whose limit ordinal is 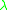 , then the generating functions can be defined
, then the generating functions can be defined 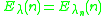 . However, this definition depends upon a standard way of defining the fundamental sequence. Rose (1984) suggests a standard way for all ordinals α < ε0.
. However, this definition depends upon a standard way of defining the fundamental sequence. Rose (1984) suggests a standard way for all ordinals α < ε0.The original extension was due to Martin Löb
Martin Löb
Martin Hugo Löb was a German mathematician. He settled in the United Kingdom after the Second World War and specialised in mathematical logic. He moved to the Netherlands in the 1970s, where he remained in retirement...
and Stan S. Wainer (1970) and is sometimes called the Löb–Wainer hierarchy.

