Growth accounting
Encyclopedia
Growth accounting is a procedure used in economics
to measure the contribution of different factors to economic growth
and to indirectly compute the rate of technological progress, measured as a residual, in an economy. This methodology was introduced by Robert Solow
in 1957
Growth accounting decomposes the growth rate of economy's total output into that which is due to increases in the amount of factors used - usually the increase in the amount of capital
and labor
- and that which cannot be accounted for by observable changes in factor utilization. The unexplained part of growth in GDP is then taken to represent increases in productivity (getting more output with the same amounts of inputs) or a measure of broadly defined technological progress.
The technique has been applied to virtually every economy in the world and a common finding is that observed levels of economic growth cannot be explained simply by changes in the stock of capital in the economy or population and labor force growth rates. Hence, technological progress plays a key role in the economic growth of nations, or the lack of it.
As an abstract example consider an economy whose total output (GDP) grows at 3% per year. Over the same period its capital stock grows at 6% per year and its labor force by 1%. The contribution of the growth rate of capital to output is equal to that growth rate weighted by the share of capital in total output and the contribution of labor is given by the growth rate of labor weighted by labor's share in income. If capital's share in output is 1/3, then labor's share is 2/3 (assuming these are the only two factors of production). This means that the portion of growth in output which is due to changes in factors is .06*(1/3)+.01*(2/3)=.027 or 2.7%. This means that there is still 0.3% of the growth in output that cannot be accounted for. This remainder is the increase in the productivity of factors that happened over the period, or the measure of technological progress during this time.
:
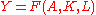
where Y is total output, K is the stock of capital in the economy, L is the labor force (or population) and A is a "catch all" factor for technology, role of institutions and other relevant forces which measures how productively capital and labor are used in production.
Standard assumptions on the form of the function F(.) is that it is increasing in K, L, A (if you increase productivity or you increase the amount of factors used you get more output) and that it is homogeneous of degree one
, or in other words that there are constant returns to scale (which means that if you double both K and L you get double the output). The assumption of constant returns to scale facilitates the assumption of perfect competition
which in turn implies that factors get their marginal products:
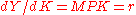
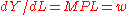
where MPK denotes the extra units of output produced with an additional unit of capital and similarly, for MPL. Wages paid to labor are denoted by w and the rate of profit or the real interest rate is denoted by r. Note that the assumption of perfect competition
enables us to take prices as given. For simplicity we assume unit price (i.e. P =1), and thus quantities also represent values in all equations.
If we totally differentiate the above production function we get;
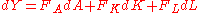
where
denotes the partial derivative with respect to factor i, or for the case of capital and labor, the marginal products. With perfect competition this equation becomes:
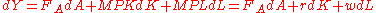
If we divide through by Y and convert each change into growth rates we get:
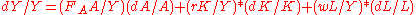
or denoting a growth rate (percentage change over time) of a factor as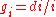
we get:
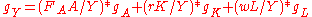
Then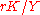
is the share of total income that goes to capital, which can be denoted as 
and 
is the share of total income that goes to labor, denoted by 
. This allows us to express the above equation as:
In principle the terms
, 
, 
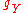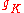and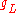 
are all observable and can be measured using standard national income accounting
methods (with capital stock being measured using investment rates via the perpetual inventory method). The term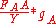
however is not directly observable as it captures technological growth and improvement in productivity that are unrelated to changes in use of factors. This term is usually referred to as Solow residual
or Total factor productivity
growth. Slightly rearranging the previous equation we can measure this as that portion of increase in total output which is not due to the (weighted) growth of factor inputs:
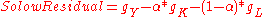
Another way to express the same idea is in per capita (or per worker) terms in which we subtract off the growth rate of labor force from both sides:
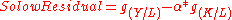
which states that the rate of technological growth is that part of the growth rate of per capita income which is not due to the (weighted) growth rate of capital per person.
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
to measure the contribution of different factors to economic growth
Economic growth
In economics, economic growth is defined as the increasing capacity of the economy to satisfy the wants of goods and services of the members of society. Economic growth is enabled by increases in productivity, which lowers the inputs for a given amount of output. Lowered costs increase demand...
and to indirectly compute the rate of technological progress, measured as a residual, in an economy. This methodology was introduced by Robert Solow
Robert Solow
Robert Merton Solow is an American economist particularly known for his work on the theory of economic growth that culminated in the exogenous growth model named after him...
in 1957
Growth accounting decomposes the growth rate of economy's total output into that which is due to increases in the amount of factors used - usually the increase in the amount of capital
Capital (economics)
In economics, capital, capital goods, or real capital refers to already-produced durable goods used in production of goods or services. The capital goods are not significantly consumed, though they may depreciate in the production process...
and labor
Labor force
In economics, a labor force or labour force is a region's combined civilian workforce, including both the employed and unemployed.Normally, the labor force of a country consists of everyone of working age In economics, a labor force or labour force is a region's combined civilian workforce,...
- and that which cannot be accounted for by observable changes in factor utilization. The unexplained part of growth in GDP is then taken to represent increases in productivity (getting more output with the same amounts of inputs) or a measure of broadly defined technological progress.
The technique has been applied to virtually every economy in the world and a common finding is that observed levels of economic growth cannot be explained simply by changes in the stock of capital in the economy or population and labor force growth rates. Hence, technological progress plays a key role in the economic growth of nations, or the lack of it.
Example
Technical derivation
The total output of an economy is modeled as being produced by various factors of production, with capital and Labor force being the primary ones in modern economies (although land and natural resources can also be included). This is usually captured by an aggregate production functionProduction function
In microeconomics and macroeconomics, a production function is a function that specifies the output of a firm, an industry, or an entire economy for all combinations of inputs...
:
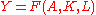
where Y is total output, K is the stock of capital in the economy, L is the labor force (or population) and A is a "catch all" factor for technology, role of institutions and other relevant forces which measures how productively capital and labor are used in production.
Standard assumptions on the form of the function F(.) is that it is increasing in K, L, A (if you increase productivity or you increase the amount of factors used you get more output) and that it is homogeneous of degree one
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
, or in other words that there are constant returns to scale (which means that if you double both K and L you get double the output). The assumption of constant returns to scale facilitates the assumption of perfect competition
Perfect competition
In economic theory, perfect competition describes markets such that no participants are large enough to have the market power to set the price of a homogeneous product. Because the conditions for perfect competition are strict, there are few if any perfectly competitive markets...
which in turn implies that factors get their marginal products:
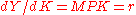
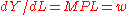
where MPK denotes the extra units of output produced with an additional unit of capital and similarly, for MPL. Wages paid to labor are denoted by w and the rate of profit or the real interest rate is denoted by r. Note that the assumption of perfect competition
Perfect competition
In economic theory, perfect competition describes markets such that no participants are large enough to have the market power to set the price of a homogeneous product. Because the conditions for perfect competition are strict, there are few if any perfectly competitive markets...
enables us to take prices as given. For simplicity we assume unit price (i.e. P =1), and thus quantities also represent values in all equations.
If we totally differentiate the above production function we get;
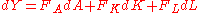
where
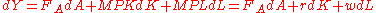
denotes the partial derivative with respect to factor i, or for the case of capital and labor, the marginal products. With perfect competition this equation becomes:If we divide through by Y and convert each change into growth rates we get:
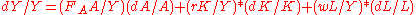
or denoting a growth rate (percentage change over time) of a factor as
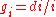we get: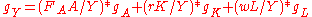Then
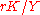is the share of total income that goes to capital, which can be denoted as and is the share of total income that goes to labor, denoted by . This allows us to express the above equation as:In principle the terms
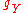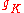, , and 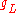are all observable and can be measured using standard national income accountingNational accounts
National accounts or national account systems are the implementation of complete and consistent accounting techniques for measuring the economic activity of a nation. These include detailed underlying measures that rely on double-entry accounting...
methods (with capital stock being measured using investment rates via the perpetual inventory method). The term
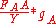however is not directly observable as it captures technological growth and improvement in productivity that are unrelated to changes in use of factors. This term is usually referred to as Solow residualSolow residual
The Solow residual is a number describing empirical productivity growth in an economy from year to year and decade to decade. Robert Solow defined rising productivity as rising output with constant capital and labor input...
or Total factor productivity
Total factor productivity
In economics, total-factor productivity is a variable which accounts for effects in total output not caused by inputs. If all inputs are accounted for, then total factor productivity can be taken as a measure of an economy’s long-term technological change or technological dynamism.If all inputs...
growth. Slightly rearranging the previous equation we can measure this as that portion of increase in total output which is not due to the (weighted) growth of factor inputs:
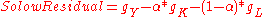
Another way to express the same idea is in per capita (or per worker) terms in which we subtract off the growth rate of labor force from both sides:
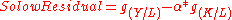
which states that the rate of technological growth is that part of the growth rate of per capita income which is not due to the (weighted) growth rate of capital per person.