Group of rational points on the unit circle
Encyclopedia
The rational point
s on the unit circle
are those points (x, y) such that both x and y are rational number
s (fractions) and satisfy x2 + y2 = 1. The set of such points turns out to be closely related to primitive Pythagorean triple
s. Consider a primitive right triangle
, that is, with integral side lengths a, b, c, with c the hypotenuse, such that the sides have no common factor larger than 1. Then on the unit circle there exists the rational point (a/c, b/c). Conversely, if (x, y) is a rational point on the unit circle, then there exists a primitive right triangle with sides xc, yc, c.
(A) and y = sin
(A), where A is the angle the radius vector (x, y) makes with the radius vector (1,0), measured counter clockwise. So with (x, y) and (t, u) forming angles A and B, respectively, with (1, 0), their sum (xt − uy, xu + yt) is just the rational point on the unit circle with angle A + B (ordinary sum).
s. If C4 denotes the cyclic subgroup with four elements generated by the point (0, 1), and Z is any infinite cyclic subgroup generated by a point of form
where 
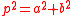is the square of a prime of form 4k + 1, (and a, b are positive) then G is isomorphic to C4 ⊕ Z ⊕ Z ⊕ ..., going on forever. Since it is an direct sum
rather than direct product
, only finitely many of the values in the Zs differ from zero.
Rational point
In number theory, a K-rational point is a point on an algebraic variety where each coordinate of the point belongs to the field K. This means that, if the variety is given by a set of equationsthen the K-rational points are solutions ∈Kn of the equations...
s on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
are those points (x, y) such that both x and y are rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (fractions) and satisfy x2 + y2 = 1. The set of such points turns out to be closely related to primitive Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s. Consider a primitive right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
, that is, with integral side lengths a, b, c, with c the hypotenuse, such that the sides have no common factor larger than 1. Then on the unit circle there exists the rational point (a/c, b/c). Conversely, if (x, y) is a rational point on the unit circle, then there exists a primitive right triangle with sides xc, yc, c.
Group operation
The set of rational points forms an infinite abelian group, which shall be called G in this article. The identity element is the point (1, 0). The group operation, or "sum" is (x, y) + (t, u) = (xt − uy, xu + yt). This is angle addition since x = cosCos
-Maths, science and technology:* Cosine, a trigonometric function* COS cells, a cell line used by biologists* Carbonyl sulfide, a chemical compound* Class of service , a 3 bit field within a layer two Ethernet frame header defined by IEEE 802.1p...
(A) and y = sin
Sin
In religion, sin is the violation or deviation of an eternal divine law or standard. The term sin may also refer to the state of having committed such a violation. Christians believe the moral code of conduct is decreed by God In religion, sin (also called peccancy) is the violation or deviation...
(A), where A is the angle the radius vector (x, y) makes with the radius vector (1,0), measured counter clockwise. So with (x, y) and (t, u) forming angles A and B, respectively, with (1, 0), their sum (xt − uy, xu + yt) is just the rational point on the unit circle with angle A + B (ordinary sum).
Group structure
The structure of G is an infinite sum of cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s. If C4 denotes the cyclic subgroup with four elements generated by the point (0, 1), and Z is any infinite cyclic subgroup generated by a point of form
where 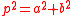is the square of a prime of form 4k + 1, (and a, b are positive) then G is isomorphic to C4 ⊕ Z ⊕ Z ⊕ ..., going on forever. Since it is an direct sumDirect sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
rather than direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
, only finitely many of the values in the Zs differ from zero.