Grothendieck universe
Encyclopedia
In mathematics
, a Grothendieck universe is a set U with the following properties:
A Grothendieck universe is meant to provide a set in which all of mathematics can be performed. (In fact, it provides a model
for set theory.) As an example, we will prove an easy proposition.
Proposition 1.
Proof.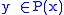
because 
. 
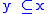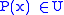because 
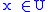, so 
.
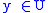It is similarly easy to prove that any Grothendieck universe U contains:
In particular, it follows from the last axiom that if U is non-empty, it must contain all of its finite subsets and a subset of each finite cardinality. One can also prove immediately from the definitions that the intersection of any class of universes is a universe.
The idea of universes is due to Alexander Grothendieck
, who used them as a way of avoiding proper classes in algebraic geometry
.
Other examples are more difficult to construct. Loosely speaking, this is because Grothendieck universes are equivalent to strongly inaccessible cardinal
s. More formally, the following two axioms are equivalent:
To prove this fact, we introduce the function c(U). Define: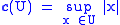
where by |x| we mean the cardinality of x. Then for any universe U, c(U) is strongly inaccessible: It is a strong limit cardinal because the power set of any element of U is an element of U and every element of U is a subset of U. To see that it is regular, suppose that cλ is a collection of cardinals indexed by I, where the cardinality of I and of each cλ is less than c(U). Then, by the definition of c(U), I and each cλ can be replaced by an element of U. The union of elements of U indexed by an element of U is an element of U, so the sum of the cλ has the cardinality of an element of U, hence is less than c(U). By invoking the axiom of foundation, that no set is contained in itself, it can be shown that c(U) equals |U|; see Bourbaki's article, which also has a counterexample when the axiom of foundation is not assumed.
Let κ be a strongly inaccessible cardinal. Say that a set S is strictly of type κ if for any sequence sn
... 
s0 
S, |sn| < κ. (S itself corresponds to the empty sequence.) Then the set u(κ) of all sets strictly of type κ is a Grothendieck universe of cardinality κ. The proof of this fact is long, so for details, we again refer to Bourbaki's article, listed in the references.
To show that the large cardinal axiom (C) implies the universe axiom (U), choose a set x. Let x0 = x, and for each n, let xn+1 =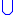
xn be the union of the elements of xn. Let y = 
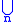xn. By (C), there is a strongly inaccessible cardinal κ such that |y| < κ. Let u(κ) be the universe of the previous paragraph. x is strictly of type κ, so x 
u(κ). To show that the universe axiom (U) implies the large cardinal axiom (C), choose a cardinal κ. κ is a set, so it is an element of a Grothendieck universe U. The cardinality of U is strongly inaccessible and strictly larger than that of κ.
In fact, any Grothendieck universe is of the form u(
) for some 
. This gives another form of the equivalence between Grothendieck universes and strongly inaccessible cardinals:
Since the existence of strongly inaccessible cardinals cannot be proved from the axioms of Zermelo-Fraenkel set theory (ZFC), the existence of universes other than the empty set and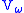
cannot be proved from ZFC either. However, strongly inaccessible cardinals are on the lower end of the list of large cardinals; thus, most set theories that use large cardinals (such as "ZFC plus there is a measurable cardinal
", "ZFC plus there are infinitely many Woodin cardinal
s") will prove that Grothendieck universes exist.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Grothendieck universe is a set U with the following properties:
- If x is an element of U and if y is an element of x, then y is also an element of U. (U is a transitive setTransitive setIn set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
.) - If x and y are both elements of U, then {x,y} is an element of U.
- If x is an element of U, then P(x), the power set of x, is also an element of U.
- If
is a family of elements of U, and if I is an element of U, then the union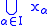 
is an element of U.
A Grothendieck universe is meant to provide a set in which all of mathematics can be performed. (In fact, it provides a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
for set theory.) As an example, we will prove an easy proposition.
Proposition 1.
- If
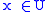and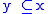 
, then 
.
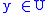Proof.
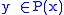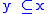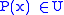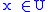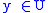because . because , so .It is similarly easy to prove that any Grothendieck universe U contains:
- All singletons of each of its elements,
- All products of all families of elements of U indexed by an element of U,
- All disjoint unions of all families of elements of U indexed by an element of U,
- All intersections of all families of elements of U indexed by an element of U,
- All functions between any two elements of U, and
- All subsets of U whose cardinal is an element of U.
In particular, it follows from the last axiom that if U is non-empty, it must contain all of its finite subsets and a subset of each finite cardinality. One can also prove immediately from the definitions that the intersection of any class of universes is a universe.
The idea of universes is due to Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, who used them as a way of avoiding proper classes in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Grothendieck universes and inaccessible cardinals
There are two simple examples of Grothendieck universes:- The empty set, and
- The set of all hereditarily finite setHereditarily finite setIn mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s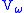
.
Other examples are more difficult to construct. Loosely speaking, this is because Grothendieck universes are equivalent to strongly inaccessible cardinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
s. More formally, the following two axioms are equivalent:
- (U) For each set x, there exists a Grothendieck universe U such that x
U. - (C) For each cardinal κ, there is a strongly inaccessible cardinal
which is strictly larger than κ.
To prove this fact, we introduce the function c(U). Define:
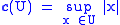
where by |x| we mean the cardinality of x. Then for any universe U, c(U) is strongly inaccessible: It is a strong limit cardinal because the power set of any element of U is an element of U and every element of U is a subset of U. To see that it is regular, suppose that cλ is a collection of cardinals indexed by I, where the cardinality of I and of each cλ is less than c(U). Then, by the definition of c(U), I and each cλ can be replaced by an element of U. The union of elements of U indexed by an element of U is an element of U, so the sum of the cλ has the cardinality of an element of U, hence is less than c(U). By invoking the axiom of foundation, that no set is contained in itself, it can be shown that c(U) equals |U|; see Bourbaki's article, which also has a counterexample when the axiom of foundation is not assumed.
Let κ be a strongly inaccessible cardinal. Say that a set S is strictly of type κ if for any sequence sn
... s0 S, |sn| < κ. (S itself corresponds to the empty sequence.) Then the set u(κ) of all sets strictly of type κ is a Grothendieck universe of cardinality κ. The proof of this fact is long, so for details, we again refer to Bourbaki's article, listed in the references.To show that the large cardinal axiom (C) implies the universe axiom (U), choose a set x. Let x0 = x, and for each n, let xn+1 =
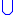xn be the union of the elements of xn. Let y = 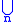xn. By (C), there is a strongly inaccessible cardinal κ such that |y| < κ. Let u(κ) be the universe of the previous paragraph. x is strictly of type κ, so x u(κ). To show that the universe axiom (U) implies the large cardinal axiom (C), choose a cardinal κ. κ is a set, so it is an element of a Grothendieck universe U. The cardinality of U is strongly inaccessible and strictly larger than that of κ.In fact, any Grothendieck universe is of the form u(
) for some . This gives another form of the equivalence between Grothendieck universes and strongly inaccessible cardinals:- For any Grothendieck universe U, |U| is either zero,
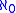, or a strongly inaccessible cardinal. And if 
is zero,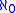 
, or a strongly inaccessible cardinal, then there is a Grothendieck universe u(
). Furthermore, u(|U|)=U, and |u(
)|=
.
Since the existence of strongly inaccessible cardinals cannot be proved from the axioms of Zermelo-Fraenkel set theory (ZFC), the existence of universes other than the empty set and
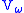cannot be proved from ZFC either. However, strongly inaccessible cardinals are on the lower end of the list of large cardinals; thus, most set theories that use large cardinals (such as "ZFC plus there is a measurable cardinalMeasurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
", "ZFC plus there are infinitely many Woodin cardinal
Woodin cardinal
In set theory, a Woodin cardinal is a cardinal number λ such that for all functionsthere exists a cardinal κ In set theory, a Woodin cardinal is a cardinal number λ such that for all functions...
s") will prove that Grothendieck universes exist.
See also
- Constructible universeConstructible universeIn mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
- Inaccessible cardinalInaccessible cardinalIn set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
- Tarski–Grothendieck set theory
- Universe (mathematics)Universe (mathematics)In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
- Von Neumann universeVon Neumann universeIn set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...