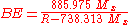Gravitational binding energy
Encyclopedia
The gravitational binding energy
of an object consisting of loose material, held together by gravity alone, is the amount of energy
required to pull all of the material apart, to infinity. It is also the amount of energy that is liberated (usually in the form of heat
) during the accretion
of such an object from material falling from infinity.
The gravitational binding energy of a system is equal to the negative of the total gravitational potential energy, considering the system as a set of small particles. For a system consisting of a celestial body and a satellite, the gravitational binding energy will have a larger absolute value than the potential energy of the satellite with respect to the celestial body, because for the latter quantity, only the separation of the two components is taken into account, keeping each intact.
For a spherical mass
of uniform density
, the gravitational binding energy U is given by the formula
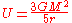
where G is the gravitational constant
, M is the mass of the sphere, and r is its radius. This is 80% greater than the energy required to separate to infinity the two hemispheres of the spherical mass.
Assuming that the Earth
is a uniform sphere (which is not correct, but is close enough to get an order-of-magnitude estimate) with M = 5.97 · 1024kg and r = 6.37 · 106m, U is 2.24 · 1032J. This is roughly equal to one week of the Sun
's total energy output. It is 37.5 MJ/kg, 60% of the absolute value of the potential energy per kilogram at the surface.
The actual depth-dependence of density, inferred from seismic travel times (see Adams–Williamson equation
), is given in the Preliminary Reference Earth Model (PREM). Using this, the real gravitational binding energy of Earth can be calculated numerically
to U = 2,487 · 1032 J
According to the virial theorem, the gravitational binding energy of a star
is about two times its internal thermal energy
.
If we assume a constant density then the masses of a shell and the sphere inside it are:
then the masses of a shell and the sphere inside it are: and
and 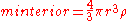
The required energy for a shell is the negative of the gravitational potential energy:

Integrating over all shells we get:
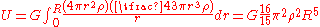
Remembering that is simply equal to the mass of the whole divided by its volume for objects with uniform density we get:
is simply equal to the mass of the whole divided by its volume for objects with uniform density we get:
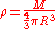
And finally, plugging this in to our result we get:
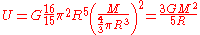
Neutron star relativistic equations of state provided by Jim Lattimer include a graph of radius vs. mass for various models. The most likely radii for a given neutron star mass are bracketed by models AP4 (smallest radius) and MS2 (largest radius). BE is the ratio of gravitational binding energy mass equivalent to observed neutron star gravitational mass of "M" kilograms with radius "R" meters,
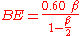

Given current values
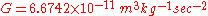

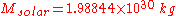
and star masses "M" commonly reported as multiples of one solar mass,
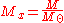
then the relativistic fractional binding energy of a neutron star is
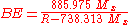
Binding energy
Binding energy is the mechanical energy required to disassemble a whole into separate parts. A bound system typically has a lower potential energy than its constituent parts; this is what keeps the system together—often this means that energy is released upon the creation of a bound state...
of an object consisting of loose material, held together by gravity alone, is the amount of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
required to pull all of the material apart, to infinity. It is also the amount of energy that is liberated (usually in the form of heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
) during the accretion
Accretion disc
An accretion disc is a structure formed by diffuse material in orbital motion around a central body. The central body is typically a star. Gravity causes material in the disc to spiral inward towards the central body. Gravitational forces compress the material causing the emission of...
of such an object from material falling from infinity.
The gravitational binding energy of a system is equal to the negative of the total gravitational potential energy, considering the system as a set of small particles. For a system consisting of a celestial body and a satellite, the gravitational binding energy will have a larger absolute value than the potential energy of the satellite with respect to the celestial body, because for the latter quantity, only the separation of the two components is taken into account, keeping each intact.
For a spherical mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of uniform density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, the gravitational binding energy U is given by the formula
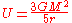
where G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, M is the mass of the sphere, and r is its radius. This is 80% greater than the energy required to separate to infinity the two hemispheres of the spherical mass.
Assuming that the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is a uniform sphere (which is not correct, but is close enough to get an order-of-magnitude estimate) with M = 5.97 · 1024kg and r = 6.37 · 106m, U is 2.24 · 1032J. This is roughly equal to one week of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
's total energy output. It is 37.5 MJ/kg, 60% of the absolute value of the potential energy per kilogram at the surface.
The actual depth-dependence of density, inferred from seismic travel times (see Adams–Williamson equation
Adams–Williamson equation
The Adams–Williamson equation, named after L. H. Adams and E. D. Williamson, is a relation between the velocities of seismic waves and the density of the Earth's interior. Given the average density of rocks at the Earth's surface and profiles of the P-wave and S-wave speeds as function of depth,...
), is given in the Preliminary Reference Earth Model (PREM). Using this, the real gravitational binding energy of Earth can be calculated numerically
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
to U = 2,487 · 1032 J
According to the virial theorem, the gravitational binding energy of a star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
is about two times its internal thermal energy
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
.
Derivation for a uniform sphere
The gravitational binding energy of a sphere is found by imagining that it is pulled apart by successively moving spherical shells to infinity, the outermost first, and finding the total energy needed for that.If we assume a constant density
 then the masses of a shell and the sphere inside it are:
then the masses of a shell and the sphere inside it are: and
and 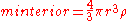
The required energy for a shell is the negative of the gravitational potential energy:

Integrating over all shells we get:
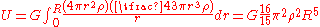
Remembering that
 is simply equal to the mass of the whole divided by its volume for objects with uniform density we get:
is simply equal to the mass of the whole divided by its volume for objects with uniform density we get: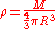
And finally, plugging this in to our result we get:
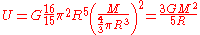
Non-uniform spheres
Planets and stars have radial density gradients from their smaller density surfaces to their much larger density compressed cores. Degenerate matter objects (white dwarfs; neutron star pulsars) have radial density gradients plus relativistic corrections. Dave Typinski demonstrates iron-cored Earth's homogeneous average density gravitational binding energy value is 31% larger than its more accurate integrated-over-density vs. radius value. The moon's homogeneous average density gravitational binding energy value is 1.8% higher than its more accurate mantle plus core radial density value.Neutron star relativistic equations of state provided by Jim Lattimer include a graph of radius vs. mass for various models. The most likely radii for a given neutron star mass are bracketed by models AP4 (smallest radius) and MS2 (largest radius). BE is the ratio of gravitational binding energy mass equivalent to observed neutron star gravitational mass of "M" kilograms with radius "R" meters,
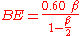

Given current values
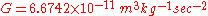

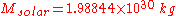
and star masses "M" commonly reported as multiples of one solar mass,
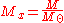
then the relativistic fractional binding energy of a neutron star is