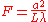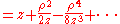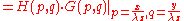Fresnel diffraction
Encyclopedia
In optics
, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction
that can be applied to the propagation of waves in the near field
.
The near field
can be specified by the Fresnel number, of the optical arrangement, which is defined, for a wave incident on an aperture, as:
where
When the diffracted wave is considered to be in the near field, and the Fresnel diffraction equation can be used to calculate its form.
the diffracted wave is considered to be in the near field, and the Fresnel diffraction equation can be used to calculate its form.
 The multiple Fresnel diffraction at nearly placed periodical ridges
The multiple Fresnel diffraction at nearly placed periodical ridges
(ridged mirror
) causes the specular reflection
; this effect can be used for atomic mirrors.
in 17th century Italy.
In his monograph entitled "Light," Richard C. MacLaurin explains Fresnel diffraction by asking what happens when light propagates, and how that process is affected when a barrier with a slit or hole in it is interposed in the beam produced by a distant source of light. He uses the Principle of Huygens to investigate, in classical terms, what transpires. The wave front that proceeds from the slit and on to a detection screen some distance away very closely approximates a wave front originating across the area of the gap without regard to any minute interactions with the actual physical edge.
The result is that if the gap is very narrow only diffraction patterns with bright centers can occur. If the gap is made progressively wider, then diffraction patterns with dark centers will alternate with diffraction patterns with bright centers. As the gap becomes larger, the differentials between dark and light bands decrease until a diffraction effect can no longer be detected.
MacLaurin does not mention the possibility that the center of the series of diffraction rings produced when light is shone through a small hole may be black, but he does point to the inverse situation wherein the shadow produced by a small circular object can paradoxically have a bright center. (p. 219)
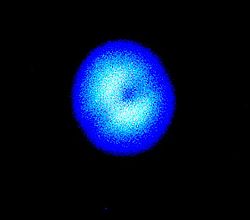
In his Optics,, Francis Weston Sears offers a mathematical approximation suggested by Fresnel that predicts the main features of diffraction patterns and uses only simple mathematics. By considering the perpendicular distance from the hole in a barrier screen to a nearby detection screen along with the wavelength of the incident light, it is possible to compute a number of regions called half-period elements or Fresnel zones. The inner zone will be a circle and each succeeding zone will be a concentric annular ring. If the diameter of the circular hole in the screen is sufficient to expose the first or central Fresnel zone, the amplitude of light at the center of the detection screen will be double what it would be if the detection screen were not obstructed. If the diameter of the circular hole in the screen is sufficient to expose two Fresnel zones, then the amplitude at the center is almost zero. That means that a Fresnel diffraction pattern can have a dark center. These patterns can be seen and measured, and correspond well to the values calculated for them. Figure 9-5, following p. 222, in Sears shows four Fraunhofer patterns in the top row followed by sixteen Fresnel diffraction patterns. Three of them have dark centers. (See the photograph above, and check the book by Sears for very much nicer photographs. A simulation can be operated by visiting http://www.temf.de/Diffraction.135.0.html?&L=1#c641)
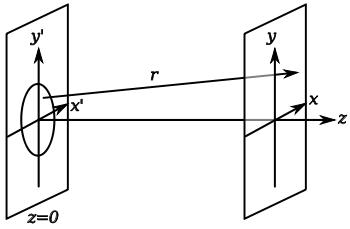 The electric field diffraction
The electric field diffraction
pattern at a point (x,y,z) is given by:
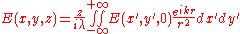
where
 , and
, and
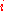 is the imaginary unit
is the imaginary unit
.
Analytical solution of this integral is impossible for all but the simplest diffraction geometries. Therefore, it is usually calculated numerically.
The main problem for solving the integral is the expression of r. First, we can simplify the algebra by introducing the substitution:

Substituting into the expression for r, we find:
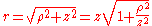
Next, using the Taylor series
expansion

we can express r as
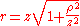
If we consider all the terms of Taylor series, then there is no approximation. Let us substitute this expression in the argument of the exponential within the integral; the key to the Fresnel approximation is to assume that the third element is very small and can be ignored. In order to make this possible, it has to contribute to the variation of the exponential for an almost null term. In other words, it has to be much smaller than the period of the complex exponential, i.e. :
:
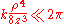
expressing k in terms of the wavelength,
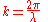
we get the following relationship:
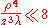
Multiplying both sides by , we have
, we have

or, substituting the earlier expression for ρ2 ,
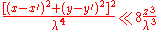
If this condition holds true for all values of x, x' , y and y' , then we can ignore the third term in the Taylor expression. Furthermore, if the third term is negligible, then all terms of higher order will be even smaller, so we can ignore them as well.
For applications involving optical wavelengths, the wavelength λ is typically many orders of magnitude smaller than the relevant physical dimensions. In particular:

and

Thus, as a practical matter, the required inequality will always hold true as long as

We can then approximate the expression with only the first two terms:

This equation, then, is the Fresnel approximation, and the inequality stated above is a condition for the approximation's validity.
The condition for validity is fairly weak, and it allows all length parameters to take comparable values, provided the aperture is small compared to the path length. For the r in the denominator we go one step further, and approximate it with only the first term, . This is valid in particular if we are interested in the behaviour of the field only in a small area close to the origin, where the values of x and y are much smaller than z. In addition, it is always valid if as well as the Fresnel condition, we have
. This is valid in particular if we are interested in the behaviour of the field only in a small area close to the origin, where the values of x and y are much smaller than z. In addition, it is always valid if as well as the Fresnel condition, we have  , where L is the distance between the aperture and the field point.
, where L is the distance between the aperture and the field point.
For Fresnel diffraction the electric field at point (x,y,z) is then given by:
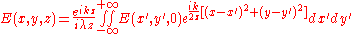
This is the Fresnel diffraction integral; it means that, if the Fresnel approximation is valid, the propagating field is a spherical wave, originating at the aperture and moving along z. The integral modulates the amplitude and phase of the spherical wave.
Analytical solution of this expression is still only possible in rare cases. For a further simplified case, valid only for much larger distances from the diffraction source see Fraunhofer diffraction
. Unlike Fraunhofer diffraction, Fresnel diffraction accounts for the curvature of the wavefront
, in order to correctly calculate the relative phase
of interfering waves.
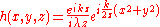
then the integral can be expressed in terms of a convolution
:
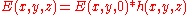
in other words we are representing the propagation using a linear-filter modeling. That is why we might call the function h(x,y,z) the impulse response of free space propagation.
. If in the integral we express k in terms of the wavelength,
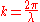
and we expand each component of the transverse displacement,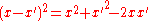
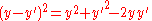
then we can express the integral in terms of the two dimensional Fourier transform. Let us use the following definition:
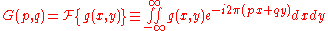
where p and q are spatial frequencies (in units of lines/meter). The Fresnel integral can be expressed as:

where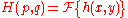
i.e. first multiply the field to be propagated for a complex exponential, calculate its two dimensional Fourier transform, replace (p,q) with and multiply it by another factor. This expression is better than the others when the process leads to a known Fourier transform, and the connection with the Fourier transform is tightened in the linear canonical transformation
and multiply it by another factor. This expression is better than the others when the process leads to a known Fourier transform, and the connection with the Fourier transform is tightened in the linear canonical transformation
, discussed below.
, Fresnel diffraction can be seen as a shear in the time-frequency domain, corresponding to how the Fourier transform is a rotation in the time-frequency domain.
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction
Kirchhoff's diffraction formula
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
that can be applied to the propagation of waves in the near field
Near field
Near field may refer to:*Near-field , an algebraic structure*Near and far field, parts of an electromagnetic field*Near field communication, a set of short-range wireless technologies, typically requiring a distance of 4 cm or less...
.
The near field
Near field
Near field may refer to:*Near-field , an algebraic structure*Near and far field, parts of an electromagnetic field*Near field communication, a set of short-range wireless technologies, typically requiring a distance of 4 cm or less...
can be specified by the Fresnel number, of the optical arrangement, which is defined, for a wave incident on an aperture, as:
where
-
 is the characteristic size of the aperture
is the characteristic size of the aperture -
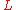 is the distance of the observation point from the aperture
is the distance of the observation point from the aperture -
 is the wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
is the wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the wave.
When
 the diffracted wave is considered to be in the near field, and the Fresnel diffraction equation can be used to calculate its form.
the diffracted wave is considered to be in the near field, and the Fresnel diffraction equation can be used to calculate its form.
(ridged mirror
Ridged mirror
In atomic physics, a ridged mirror is a kind of atomic mirror, designed for the specular reflection of neutral particles coming at the grazing incidence angle, characterised in the following: in order to reduce the mean attraction of particles to the surface and increase the reflectivity, this...
) causes the specular reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
; this effect can be used for atomic mirrors.
Early treatments of this phenomenon
Some of the earliest work on what would become known as Fresnel diffraction was carried out by Francesco Maria GrimaldiFrancesco Maria Grimaldi
Francesco Maria Grimaldi was an Italian Jesuit priest, mathematician and physicist who taught at the Jesuit college in Bologna....
in 17th century Italy.
In his monograph entitled "Light," Richard C. MacLaurin explains Fresnel diffraction by asking what happens when light propagates, and how that process is affected when a barrier with a slit or hole in it is interposed in the beam produced by a distant source of light. He uses the Principle of Huygens to investigate, in classical terms, what transpires. The wave front that proceeds from the slit and on to a detection screen some distance away very closely approximates a wave front originating across the area of the gap without regard to any minute interactions with the actual physical edge.
The result is that if the gap is very narrow only diffraction patterns with bright centers can occur. If the gap is made progressively wider, then diffraction patterns with dark centers will alternate with diffraction patterns with bright centers. As the gap becomes larger, the differentials between dark and light bands decrease until a diffraction effect can no longer be detected.
MacLaurin does not mention the possibility that the center of the series of diffraction rings produced when light is shone through a small hole may be black, but he does point to the inverse situation wherein the shadow produced by a small circular object can paradoxically have a bright center. (p. 219)
In his Optics,, Francis Weston Sears offers a mathematical approximation suggested by Fresnel that predicts the main features of diffraction patterns and uses only simple mathematics. By considering the perpendicular distance from the hole in a barrier screen to a nearby detection screen along with the wavelength of the incident light, it is possible to compute a number of regions called half-period elements or Fresnel zones. The inner zone will be a circle and each succeeding zone will be a concentric annular ring. If the diameter of the circular hole in the screen is sufficient to expose the first or central Fresnel zone, the amplitude of light at the center of the detection screen will be double what it would be if the detection screen were not obstructed. If the diameter of the circular hole in the screen is sufficient to expose two Fresnel zones, then the amplitude at the center is almost zero. That means that a Fresnel diffraction pattern can have a dark center. These patterns can be seen and measured, and correspond well to the values calculated for them. Figure 9-5, following p. 222, in Sears shows four Fraunhofer patterns in the top row followed by sixteen Fresnel diffraction patterns. Three of them have dark centers. (See the photograph above, and check the book by Sears for very much nicer photographs. A simulation can be operated by visiting http://www.temf.de/Diffraction.135.0.html?&L=1#c641)
The Fresnel diffraction integral

Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
pattern at a point (x,y,z) is given by:
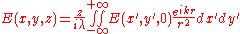
where
 , and
, and is the imaginary unit
is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
Analytical solution of this integral is impossible for all but the simplest diffraction geometries. Therefore, it is usually calculated numerically.
The Fresnel approximation
The main problem for solving the integral is the expression of r. First, we can simplify the algebra by introducing the substitution:

Substituting into the expression for r, we find:
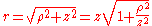
Next, using the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion

we can express r as
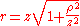
If we consider all the terms of Taylor series, then there is no approximation. Let us substitute this expression in the argument of the exponential within the integral; the key to the Fresnel approximation is to assume that the third element is very small and can be ignored. In order to make this possible, it has to contribute to the variation of the exponential for an almost null term. In other words, it has to be much smaller than the period of the complex exponential, i.e.
 :
: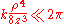
expressing k in terms of the wavelength,
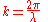
we get the following relationship:
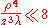
Multiplying both sides by
 , we have
, we have
or, substituting the earlier expression for ρ2 ,
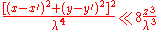
If this condition holds true for all values of x, x' , y and y' , then we can ignore the third term in the Taylor expression. Furthermore, if the third term is negligible, then all terms of higher order will be even smaller, so we can ignore them as well.
For applications involving optical wavelengths, the wavelength λ is typically many orders of magnitude smaller than the relevant physical dimensions. In particular:

and

Thus, as a practical matter, the required inequality will always hold true as long as

We can then approximate the expression with only the first two terms:

This equation, then, is the Fresnel approximation, and the inequality stated above is a condition for the approximation's validity.
Fresnel diffraction
Fresnel diffraction occurs when: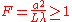 |
| Fraunhofer diffraction Fraunhofer diffraction In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.... occurs when: 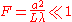 |
 - aperture or slit size, - aperture or slit size,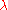 - wavelength, - wavelength,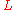 - distance from the aperture - distance from the aperture |
The condition for validity is fairly weak, and it allows all length parameters to take comparable values, provided the aperture is small compared to the path length. For the r in the denominator we go one step further, and approximate it with only the first term,
 . This is valid in particular if we are interested in the behaviour of the field only in a small area close to the origin, where the values of x and y are much smaller than z. In addition, it is always valid if as well as the Fresnel condition, we have
. This is valid in particular if we are interested in the behaviour of the field only in a small area close to the origin, where the values of x and y are much smaller than z. In addition, it is always valid if as well as the Fresnel condition, we have  , where L is the distance between the aperture and the field point.
, where L is the distance between the aperture and the field point.For Fresnel diffraction the electric field at point (x,y,z) is then given by:
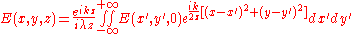
This is the Fresnel diffraction integral; it means that, if the Fresnel approximation is valid, the propagating field is a spherical wave, originating at the aperture and moving along z. The integral modulates the amplitude and phase of the spherical wave.
Analytical solution of this expression is still only possible in rare cases. For a further simplified case, valid only for much larger distances from the diffraction source see Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
. Unlike Fraunhofer diffraction, Fresnel diffraction accounts for the curvature of the wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
, in order to correctly calculate the relative phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
of interfering waves.
Convolution
The integral can be expressed in other ways in order to calculate it using some mathematical properties. If we define the following function: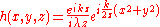
then the integral can be expressed in terms of a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
:
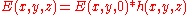
in other words we are representing the propagation using a linear-filter modeling. That is why we might call the function h(x,y,z) the impulse response of free space propagation.
Fourier transform
Another possible way is through the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. If in the integral we express k in terms of the wavelength,
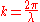
and we expand each component of the transverse displacement,
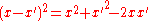
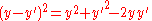
then we can express the integral in terms of the two dimensional Fourier transform. Let us use the following definition:
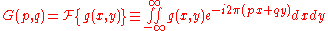
where p and q are spatial frequencies (in units of lines/meter). The Fresnel integral can be expressed as:

where
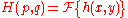
i.e. first multiply the field to be propagated for a complex exponential, calculate its two dimensional Fourier transform, replace (p,q) with
 and multiply it by another factor. This expression is better than the others when the process leads to a known Fourier transform, and the connection with the Fourier transform is tightened in the linear canonical transformation
and multiply it by another factor. This expression is better than the others when the process leads to a known Fourier transform, and the connection with the Fourier transform is tightened in the linear canonical transformationLinear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
, discussed below.
Linear canonical transformation
From the point of view of the linear canonical transformationLinear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
, Fresnel diffraction can be seen as a shear in the time-frequency domain, corresponding to how the Fourier transform is a rotation in the time-frequency domain.
See also
- Fraunhofer diffractionFraunhofer diffractionIn optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
- Fresnel integralFresnel integral250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
- Fresnel zoneFresnel zoneIn optics and radio communications , a Fresnel zone , named for physicist Augustin-Jean Fresnel, is one of a number of concentric ellipsoids which define volumes in the radiation pattern of a circular aperture...
- Fresnel numberFresnel numberThe Fresnel number F, named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory....
- Augustin-Jean FresnelAugustin-Jean FresnelAugustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....
- Ridged mirrorRidged mirrorIn atomic physics, a ridged mirror is a kind of atomic mirror, designed for the specular reflection of neutral particles coming at the grazing incidence angle, characterised in the following: in order to reduce the mean attraction of particles to the surface and increase the reflectivity, this...
- Fresnel imagerFresnel ImagerA Fresnel imager is a proposed ultra-lightweight design for a space telescope that uses a Fresnel array as primary optics instead of a typical lens. It focuses light with a thin opaque foil sheet punched with specially shaped holes, thus focusing light on a certain point by using the phenomenon of...
- Euler spiralEuler spiralAn Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....