Free lattice
Encyclopedia
In mathematics
, in the area of order theory
, a free lattice is the free object
corresponding to a lattice
. As free objects, they have the universal property
. The word problem
for free lattices is also challenging.
. The universal morphism is
, where 
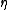the unit map 
which takes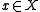 
to the singleton set 
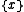. The universal property is then as follows: given any map 
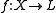from X to some arbitrary semilattice L, there exists a unique semilattice homomorphism 
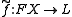such that 
. The map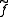 
may be explicitly written down; it is given by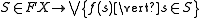
Here,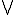
denotes the semilattice operation in L. This construction may be promoted from semilattices to lattices; by construction the map 
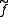will have the same properties as the lattice.
The symbol F is then a functor
from the category of sets
to the category of lattices and lattice homomorphisms. The functor F is left adjoint
to the forgetful functor
from lattices to their underlying sets. The free lattice is a free object
.
for free lattices has some interesting aspects. Consider the case of bounded lattices, i.e. algebraic structures with the two binary operations
and 
and the two constants (nullary operations) 0 and 1. The set of all correct (well-formed) expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to be equal in any lattice. For example, if a is some element of X, then a
1 = 1 and a
1 =a. The word problem for lattices is the problem of determining which of these elements of W(X) correspond to the same element.
The word problem may be resolved as follows. A relation <~ on W(X) may be defined inductively
by setting w <~ v if and only if
one of the following holds:
This defines a preorder
<~ on W(X), so we can define an equivalence relation
given by w~v when w<~v and v<~w. One may then show that the partially ordered
quotient space
W(X)/~ is the free lattice FX given above. The equivalence classes of W(X)/~ are the sets of all words w and v with w<~v and v<~w. The case of lattices that are not bounded is treated similarly, using only the two binary operations in the above construction.
The word problem on free lattices has several interesting corollaries. One is that the free lattice of a three-element set of generators is infinite. In fact, one can even show that every free lattice on three generators contains a sublattice which is free for a set of four generators. By induction
, this eventually yields a sublattice free on countably many generators. This property is reminiscent of SQ-universality in groups
.
The proof that the free lattice in three generators is infinite proceeds by inductively defining
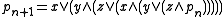
where x, y, and z are the three generators, and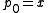
. One then shows, using the inductive relations of the word problem, that 
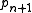is strictly greater than 
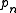, and therefore that there must be an infinite number of 
.
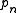in terms of relations, it does not suffice to use the finitary relations of meet and join; one must also have infinitary relations defining the meet and join of infinite subsets. For example, the infinitary relation corresponding to "join" may be defined as
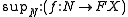
Here, f is a map from the elements of an cardinal
N to FX; the operator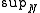
denotes the supremum, in that it takes the image of f to its join. This is, of course, identical to "join" when N is a finite number; the point of this definition is to define join as a relation, even when N is an infinite cardinal.
The axioms of the pre-ordering of the word problem may be adjoined by the two infinitary operators corresponding to meet and join. After doing so, one then extends the definition of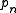
to an ordinally
indexed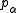
given by
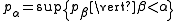
when
is a limit ordinal. Then, as before, one may show that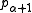 
is strictly greater than 
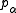. Thus, there are at least as many elements in the complete free lattice as there are ordinals, and thus, the complete free lattice cannot exist as a set, and must therefore be a proper class.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a free lattice is the free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
corresponding to a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. As free objects, they have the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. The word problem
Word problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
for free lattices is also challenging.
Formal definition
Any set X may be used to generate the free semilattice FX. The free semilattice is defined to consist of all of the finite subsets of X, with the semilattice operation given by ordinary set union. The free semilattice has the universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. The universal morphism is
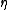, where the unit map which takes 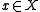to the singleton set 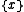. The universal property is then as follows: given any map 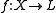from X to some arbitrary semilattice L, there exists a unique semilattice homomorphism 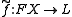such that . The map 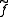may be explicitly written down; it is given by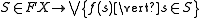Here,
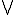denotes the semilattice operation in L. This construction may be promoted from semilattices to lattices; by construction the map 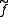will have the same properties as the lattice.The symbol F is then a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
to the category of lattices and lattice homomorphisms. The functor F is left adjoint
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from lattices to their underlying sets. The free lattice is a free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
.
Word problem
The word problemWord problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
for free lattices has some interesting aspects. Consider the case of bounded lattices, i.e. algebraic structures with the two binary operations
and and the two constants (nullary operations) 0 and 1. The set of all correct (well-formed) expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to be equal in any lattice. For example, if a is some element of X, then a1 = 1 and a1 =a. The word problem for lattices is the problem of determining which of these elements of W(X) correspond to the same element.The word problem may be resolved as follows. A relation <~ on W(X) may be defined inductively
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
by setting w <~ v if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of S),
- w = 0 or v = 1,
- w = w1
w2 and both w1<~v and w2<~v hold, - w = w1
w2 and either w1<~v or w2<~v holds, - v = v1
v2 and either w<~v1 or w<~v2 holds, - v = v1
v2 and both w<~v1 and w<~v2 hold.
This defines a preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
<~ on W(X), so we can define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
given by w~v when w<~v and v<~w. One may then show that the partially ordered
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
W(X)/~ is the free lattice FX given above. The equivalence classes of W(X)/~ are the sets of all words w and v with w<~v and v<~w. The case of lattices that are not bounded is treated similarly, using only the two binary operations in the above construction.
The word problem on free lattices has several interesting corollaries. One is that the free lattice of a three-element set of generators is infinite. In fact, one can even show that every free lattice on three generators contains a sublattice which is free for a set of four generators. By induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, this eventually yields a sublattice free on countably many generators. This property is reminiscent of SQ-universality in groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
The proof that the free lattice in three generators is infinite proceeds by inductively defining
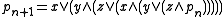
where x, y, and z are the three generators, and
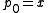. One then shows, using the inductive relations of the word problem, that 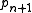is strictly greater than 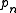, and therefore that there must be an infinite number of 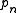.The complete free lattice
Another corollary is that the complete free lattice "does not exist", in the sense that it is instead a proper class. The proof of this follows from the word problem as well. To define a complete latticeComplete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
in terms of relations, it does not suffice to use the finitary relations of meet and join; one must also have infinitary relations defining the meet and join of infinite subsets. For example, the infinitary relation corresponding to "join" may be defined as
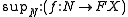
Here, f is a map from the elements of an cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
N to FX; the operator
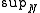denotes the supremum, in that it takes the image of f to its join. This is, of course, identical to "join" when N is a finite number; the point of this definition is to define join as a relation, even when N is an infinite cardinal.The axioms of the pre-ordering of the word problem may be adjoined by the two infinitary operators corresponding to meet and join. After doing so, one then extends the definition of
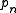to an ordinallyOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
indexed
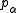given by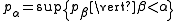when
is a limit ordinal. Then, as before, one may show that 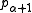is strictly greater than 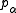. Thus, there are at least as many elements in the complete free lattice as there are ordinals, and thus, the complete free lattice cannot exist as a set, and must therefore be a proper class.