
Flow network
Encyclopedia
In graph theory
, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, except when it is a source, which has more outgoing flow, or sink, which has more incoming flow. A network can be used to model traffic in a road system, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes.
 is a finite directed graph
is a finite directed graph
in which every edge has a non-negative, real-valued capacity
has a non-negative, real-valued capacity  . If
. If  , we assume that
, we assume that  . We distinguish two vertices: a source
. We distinguish two vertices: a source  and a sink
and a sink  . A flow network is a real
. A flow network is a real
function
 with the following three properties for all nodes
with the following three properties for all nodes  and
and  :
:
Notice that is the net flow from
is the net flow from  to
to  . If the graph represents a physical network, and if there is a real flow of, for example, 4 units from
. If the graph represents a physical network, and if there is a real flow of, for example, 4 units from  to
to  , and a real flow of 3 units from
, and a real flow of 3 units from  to
to  , we have
, we have  and
and  .
.
The residual capacity of an edge is . This defines a residual network denoted
. This defines a residual network denoted  , giving the amount of available capacity. See that there can be an edge from
, giving the amount of available capacity. See that there can be an edge from  to
to  in the residual network, even though there is no edge from
in the residual network, even though there is no edge from  to
to  in the original network. Since flows in opposite directions cancel out, decreasing the flow from
in the original network. Since flows in opposite directions cancel out, decreasing the flow from  to
to  is the same as increasing the flow from
is the same as increasing the flow from  to
to  . An augmenting path is a path
. An augmenting path is a path  in the residual network, where
in the residual network, where  ,
,  , and
, and  . A network is at maximum flow if and only if there is no augmenting path in the residual network.
. A network is at maximum flow if and only if there is no augmenting path in the residual network.
Should one need to model a network with more than one source, a supersource is introduced to the graph. This consists of a vertex connected to each of the sources with edges of infinite capacity, so as to act as a global source. A similar construct for sinks is called a supersink.
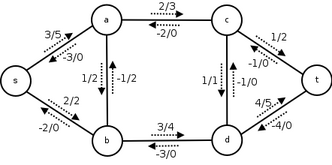 To the right you see a flow network with source labeled
To the right you see a flow network with source labeled  , sink
, sink  , and four additional nodes. The flow and capacity is denoted
, and four additional nodes. The flow and capacity is denoted  . Notice how the network upholds skew symmetry, capacity constraints and flow conservation. The total amount of flow from
. Notice how the network upholds skew symmetry, capacity constraints and flow conservation. The total amount of flow from  to
to  is 5, which can be easily seen from the fact that the total outgoing flow from
is 5, which can be easily seen from the fact that the total outgoing flow from  is 5, which is also the incoming flow to
is 5, which is also the incoming flow to  . We know that no flow appears or disappears in any of the other nodes.
. We know that no flow appears or disappears in any of the other nodes.
Below you see the residual network for the given flow. Notice how there is positive residual capacity on some edges where the original capacity is zero, for example for the edge . This flow is not a maximum flow. There is available capacity along the paths
. This flow is not a maximum flow. There is available capacity along the paths  ,
,  and
and  , which are then the augmenting paths. The residual capacity of the first path is
, which are then the augmenting paths. The residual capacity of the first path is

 . Notice that augmenting path
. Notice that augmenting path  does not exist in the original network, but you can send flow along it, and still get a legal flow.
does not exist in the original network, but you can send flow along it, and still get a legal flow.
If this is a real network, there might actually be a flow of 2 from to
to  , and a flow of 1 from
, and a flow of 1 from  to
to  , but we only maintain the net flow.
, but we only maintain the net flow.
Flows can pertain to people or material over transportation networks, or to electricity over electrical distribution systems. For any such physical network, the flow coming into any intermediate node needs to equal the flow going out of that node. This conservation constraint was formalized as Kirchhoff's current law.
Flow networks also find applications in ecology
: flow networks arise naturally when considering the flow of nutrients and energy between different organizations in a food web
. The mathematical problems associated with such networks are quite different from those that arise in networks of fluid or traffic flow. The field of ecosystem network analysis, developed by Robert Ulanowicz
and others, involves using concepts from information theory
and thermodynamics
to study the evolution of these networks over time.
The simplest and most common problem using flow networks is to find what is called the maximum flow
, which provides the largest possible total flow from the source to the sink in a given graph. There are many other problems which can be solved using max flow algorithms, if they are appropriately modeled as flow networks, such as bipartite matching, the assignment problem
and the transportation problem.
In a multi-commodity flow problem
, you have multiple sources and sinks, and various "commodities" which are to flow from a given source to a given sink. This could be for example various goods that are produced at various factories, and are to be delivered to various given customers through the same transportation network.
In a minimum cost flow problem
, each edge has a given cost
has a given cost  , and the cost of sending the flow
, and the cost of sending the flow  across the edge is
across the edge is  . The objective is to send a given amount of flow from the source to the sink, at the lowest possible price.
. The objective is to send a given amount of flow from the source to the sink, at the lowest possible price.
In a circulation problem
, you have a lower bound on the edges, in addition to the upper bound
on the edges, in addition to the upper bound  . Each edge also has a cost. Often, flow conservation holds for all nodes in a circulation problem, and there is a connection from the sink back to the source. In this way, you can dictate the total flow with
. Each edge also has a cost. Often, flow conservation holds for all nodes in a circulation problem, and there is a connection from the sink back to the source. In this way, you can dictate the total flow with  and
and  . The flow circulates through the network, hence the name of the problem.
. The flow circulates through the network, hence the name of the problem.
In a network with gains or generalized network each edge has a gain
, a real number (not zero) such that, if the edge has gain g, and an amount x flows into the edge at its tail, then an amount gx flows out at the head.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, except when it is a source, which has more outgoing flow, or sink, which has more incoming flow. A network can be used to model traffic in a road system, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes.
Definition
 is a finite directed graph
is a finite directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
in which every edge
 has a non-negative, real-valued capacity
has a non-negative, real-valued capacity  . If
. If  , we assume that
, we assume that  . We distinguish two vertices: a source
. We distinguish two vertices: a source  and a sink
and a sink  . A flow network is a real
. A flow network is a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 with the following three properties for all nodes
with the following three properties for all nodes  and
and  :
:| Capacity constraints: |  . The flow along an edge cannot exceed its capacity. . The flow along an edge cannot exceed its capacity. |
| Skew symmetry: |  . The net flow from . The net flow from  to to  must be the opposite of the net flow from must be the opposite of the net flow from  to to  (see example). (see example). |
| Flow conservation: |  , unless , unless  or or  . The net flow to a node is zero, except for the source, which "produces" flow, and the sink, which "consumes" flow. . The net flow to a node is zero, except for the source, which "produces" flow, and the sink, which "consumes" flow. |
Notice that
 is the net flow from
is the net flow from  to
to  . If the graph represents a physical network, and if there is a real flow of, for example, 4 units from
. If the graph represents a physical network, and if there is a real flow of, for example, 4 units from  to
to  , and a real flow of 3 units from
, and a real flow of 3 units from  to
to  , we have
, we have  and
and  .
.The residual capacity of an edge is
 . This defines a residual network denoted
. This defines a residual network denoted  , giving the amount of available capacity. See that there can be an edge from
, giving the amount of available capacity. See that there can be an edge from  to
to  in the residual network, even though there is no edge from
in the residual network, even though there is no edge from  to
to  in the original network. Since flows in opposite directions cancel out, decreasing the flow from
in the original network. Since flows in opposite directions cancel out, decreasing the flow from  to
to  is the same as increasing the flow from
is the same as increasing the flow from  to
to  . An augmenting path is a path
. An augmenting path is a path  in the residual network, where
in the residual network, where  ,
,  , and
, and  . A network is at maximum flow if and only if there is no augmenting path in the residual network.
. A network is at maximum flow if and only if there is no augmenting path in the residual network.Should one need to model a network with more than one source, a supersource is introduced to the graph. This consists of a vertex connected to each of the sources with edges of infinite capacity, so as to act as a global source. A similar construct for sinks is called a supersink.
Example

 , sink
, sink  , and four additional nodes. The flow and capacity is denoted
, and four additional nodes. The flow and capacity is denoted  . Notice how the network upholds skew symmetry, capacity constraints and flow conservation. The total amount of flow from
. Notice how the network upholds skew symmetry, capacity constraints and flow conservation. The total amount of flow from  to
to  is 5, which can be easily seen from the fact that the total outgoing flow from
is 5, which can be easily seen from the fact that the total outgoing flow from  is 5, which is also the incoming flow to
is 5, which is also the incoming flow to  . We know that no flow appears or disappears in any of the other nodes.
. We know that no flow appears or disappears in any of the other nodes.Below you see the residual network for the given flow. Notice how there is positive residual capacity on some edges where the original capacity is zero, for example for the edge
 . This flow is not a maximum flow. There is available capacity along the paths
. This flow is not a maximum flow. There is available capacity along the paths  ,
,  and
and  , which are then the augmenting paths. The residual capacity of the first path is
, which are then the augmenting paths. The residual capacity of the first path is
 . Notice that augmenting path
. Notice that augmenting path  does not exist in the original network, but you can send flow along it, and still get a legal flow.
does not exist in the original network, but you can send flow along it, and still get a legal flow.If this is a real network, there might actually be a flow of 2 from
 to
to  , and a flow of 1 from
, and a flow of 1 from  to
to  , but we only maintain the net flow.
, but we only maintain the net flow.Applications
Picture a series of water pipes, fitting into a network. Each pipe is of a certain diameter, so it can only maintain a flow of a certain amount of water. Anywhere that pipes meet, the total amount of water coming into that junction must be equal to the amount going out, otherwise we would quickly run out of water, or we would have a build up of water. We have a water inlet, which is the source, and an outlet, the sink. A flow would then be one possible way for water to get from source to sink so that the total amount of water coming out of the outlet is consistent. Intuitively, the total flow of a network is the rate at which water comes out of the outlet.Flows can pertain to people or material over transportation networks, or to electricity over electrical distribution systems. For any such physical network, the flow coming into any intermediate node needs to equal the flow going out of that node. This conservation constraint was formalized as Kirchhoff's current law.
Flow networks also find applications in ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
: flow networks arise naturally when considering the flow of nutrients and energy between different organizations in a food web
Food web
A food web depicts feeding connections in an ecological community. Ecologists can broadly lump all life forms into one of two categories called trophic levels: 1) the autotrophs, and 2) the heterotrophs...
. The mathematical problems associated with such networks are quite different from those that arise in networks of fluid or traffic flow. The field of ecosystem network analysis, developed by Robert Ulanowicz
Robert Ulanowicz
Robert Edward Ulanowicz is an American theoretical ecologist and philosopher who is best known for his search for a unified theory of ecology. He was born September 17, 1943 in Baltimore, Maryland....
and others, involves using concepts from information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
to study the evolution of these networks over time.
The simplest and most common problem using flow networks is to find what is called the maximum flow
Maximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum....
, which provides the largest possible total flow from the source to the sink in a given graph. There are many other problems which can be solved using max flow algorithms, if they are appropriately modeled as flow networks, such as bipartite matching, the assignment problem
Assignment problem
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics...
and the transportation problem.
In a multi-commodity flow problem
Multi-commodity flow problem
The multi-commodity flow problem is a network flow problem with multiple commodities flowing through the network, with different source and sink nodes.-Definition:Given a flow network \,G, where edge \in E has capacity \,c...
, you have multiple sources and sinks, and various "commodities" which are to flow from a given source to a given sink. This could be for example various goods that are produced at various factories, and are to be delivered to various given customers through the same transportation network.
In a minimum cost flow problem
Minimum cost flow problem
The minimum-cost flow problem is finding the cheapest possible way of sending a certain amount of flow through a flow network.- Definition :Given a flow network \,G with source s \in V and sink t \in V, where edge \in E has capacity \,c, flow \,f and cost \,a. The cost of sending this flow is f...
, each edge
 has a given cost
has a given cost  , and the cost of sending the flow
, and the cost of sending the flow  across the edge is
across the edge is  . The objective is to send a given amount of flow from the source to the sink, at the lowest possible price.
. The objective is to send a given amount of flow from the source to the sink, at the lowest possible price.In a circulation problem
Circulation problem
The circulation problem and its variants is a generalisation of network flow problems, with the added constraint of a lower bound on edge flows, and with flow conservation also being required for the source and sink...
, you have a lower bound
 on the edges, in addition to the upper bound
on the edges, in addition to the upper bound  . Each edge also has a cost. Often, flow conservation holds for all nodes in a circulation problem, and there is a connection from the sink back to the source. In this way, you can dictate the total flow with
. Each edge also has a cost. Often, flow conservation holds for all nodes in a circulation problem, and there is a connection from the sink back to the source. In this way, you can dictate the total flow with  and
and  . The flow circulates through the network, hence the name of the problem.
. The flow circulates through the network, hence the name of the problem.In a network with gains or generalized network each edge has a gain
Gain graph
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
, a real number (not zero) such that, if the edge has gain g, and an amount x flows into the edge at its tail, then an amount gx flows out at the head.
See also
- Constructal theoryConstructal theoryThe constructal law puts forth the idea that the generation of design in nature is a physics phenomenon that unites all animate and inanimate systems, and that this phenomenon is covered by the Constructal Law...
- Ford-Fulkerson algorithmFord-Fulkerson algorithmThe Ford–Fulkerson Method computes the maximum flow in a flow network. It was published in 1956...
- Flow (computer networking)Flow (computer networking)In packet switching networks, traffic flow, packet flow or network flow is a sequence of packets from a source computer to a destination, which may be another host, a multicast group, or a broadcast domain...
- Max-flow min-cut theoremMax-flow min-cut theoremIn optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
- Oriented matroidOriented matroidAn oriented matroid is a mathematical structure that abstracts the properties of directed graphs and of arrangements of vectors in a vector space over an ordered field...
- Shortest path problemShortest path problemIn graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
External links
- Maximum Flow Problem
- Maximum Flow
- Real graph instances
- Software, papers, test graphs, etc.
- [ftp://dimacs.rutgers.edu/pub/netflow Solutions for network flow problems]
- Software and papers for network flow problems
- Lemon C++ library with several maximum flow and minimum cost circulation algorithms
- QuickGraph, graph data structures and algorithms for .Net

