Five lemma
Encyclopedia
In mathematics
, especially homological algebra
and other applications of abelian category
theory, the five lemma is an important and widely used lemma
about commutative diagram
s.
The five lemma is valid not only for abelian categories but also works in the category of groups
, for example.
The five lemma can be thought of as a combination of two other theorems, the four lemmas, which are dual to each other.
in any abelian category
(such as the category of abelian group
s or the category of vector space
s over a given field) or in the category of group
s.
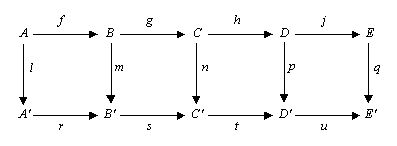
The five lemma states that, if the rows are exact
, m and p are isomorphism
s, l is an epimorphism
, and q is a monomorphism
, then n is also an isomorphism.
The two four-lemmas state:
(1) If the rows in the commutative diagram

are exact and m and p are epimorphisms and q is a monomorphism, then n is an epimorphism.
(2) If the rows in the commutative diagram

are exact and m and p are monomorphisms and l is an epimorphism, then n is a monomorphism.
To perform diagram chasing, we assume that we are in a category of modules
over some ring
, so that we may speak of elements of the objects in the diagram and think of the morphisms of the diagram as function
s (in fact, homomorphism
s) acting on those elements.
Then a morphism is a monomorphism if and only if
it is injective, and it is an epimorphism if and only if it is surjective.
Similarly, to deal with exactness, we can think of kernel
s and images in a function-theoretic sense.
The proof will still apply to any (small) abelian category because of Mitchell's embedding theorem
, which states that any small abelian category can be represented as a category of modules over some ring.
For the category of groups, just turn all additive notation below into multiplicative notation, and note that commutativity is never used.
So, to prove (1), assume that m and p are surjective and q is injective.

Then, to prove (2), assume that m and p are injective and l is surjective.

Combining the 2 four lemmas now proves the entire five lemma.
or cohomology of a given object, one typically employs a simpler subobject whose homology/cohomology is known, and arrives at a long exact sequence which involves the unknown homology groups of the original object. This alone is often not sufficient to determine the unknown homology groups, but if one can compare the original object and sub object to well-understood ones via morphisms, then a morphism between the respective long exact sequences is induced, and the five lemma can then be used to determine the unknown homology groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and other applications of abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
theory, the five lemma is an important and widely used lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
about commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
s.
The five lemma is valid not only for abelian categories but also works in the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, for example.
The five lemma can be thought of as a combination of two other theorems, the four lemmas, which are dual to each other.
Statements
Consider the following commutative diagramCommutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
in any abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
(such as the category of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or the category of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a given field) or in the category of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s.

The five lemma states that, if the rows are exact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
, m and p are isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s, l is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, and q is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, then n is also an isomorphism.
The two four-lemmas state:
(1) If the rows in the commutative diagram

are exact and m and p are epimorphisms and q is a monomorphism, then n is an epimorphism.
(2) If the rows in the commutative diagram

are exact and m and p are monomorphisms and l is an epimorphism, then n is a monomorphism.
Proof
The method of proof we shall use is commonly referred to as diagram chasing. Although it may boggle the mind at first, once one has some practice at it, it is actually fairly routine. We shall prove the five lemma by individually proving each of the 2 four lemmas.To perform diagram chasing, we assume that we are in a category of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over some ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, so that we may speak of elements of the objects in the diagram and think of the morphisms of the diagram as function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s (in fact, homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s) acting on those elements.
Then a morphism is a monomorphism if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is injective, and it is an epimorphism if and only if it is surjective.
Similarly, to deal with exactness, we can think of kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
s and images in a function-theoretic sense.
The proof will still apply to any (small) abelian category because of Mitchell's embedding theorem
Mitchell's embedding theorem
Mitchell's embedding theorem, also known as the Freyd–Mitchell theorem, is a result stating that every abelian category admits a full and exact embedding into the category of R-modules...
, which states that any small abelian category can be represented as a category of modules over some ring.
For the category of groups, just turn all additive notation below into multiplicative notation, and note that commutativity is never used.
So, to prove (1), assume that m and p are surjective and q is injective.

- Let c′ be an element of C′.
- Since p is surjective, there exists an element d in D with p(d) = t(c′).
- By commutativity of the diagram, u(p(d)) = q(j(d)).
- Since im t = ker u by exactness, 0 = u(t(c′)) = u(p(d)) = q(j(d)).
- Since q is injective, j(d) = 0, so d is in ker j = im h.
- Therefore there exists c in C with h(c) = d.
- Then t(n(c)) = p(h(c)) = t(c′). Since t is a homomorphism, it follows that t(c′ − n(c)) = 0.
- By exactness, c′ − n(c) is in the image of s, so there exists b′ in B′ with s(b′) = c′ − n(c).
- Since m is surjective, we can find b in B such that b′ = m(b).
- By commutativity, n(g(b)) = s(m(b)) = c − n(c).
- Since n is a homomorphism, n(g(b) + c) = n(g(b)) + n(c) = c′ − n(c) + n(c) = c′.
- Therefore, n is surjective.
Then, to prove (2), assume that m and p are injective and l is surjective.

- Let c in C be such that n(c) = 0.
- t(n(c)) is then 0.
- By commutativity, p(h(c)) = 0.
- Since p is injective, h(c) = 0.
- By exactness, there is an element b of B such that g(b) = c.
- By commutativity, s(m(b)) = n(g(b)) = n(c) = 0.
- By exactness, there is then an element a′ of A′ such that r(a′) = m(b).
- Since l is surjective, there is a in A such that l(a) = a′.
- By commutativity, m(f(a)) = r(l(a)) = m(b).
- Since m is injective, f(a) = b.
- So c = g(f(a)).
- Since the composition of g and f is trivial, c = 0.
- Therefore, n is injective.
Combining the 2 four lemmas now proves the entire five lemma.
Applications
The five lemma is often applied to long exact sequences: when computing homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
or cohomology of a given object, one typically employs a simpler subobject whose homology/cohomology is known, and arrives at a long exact sequence which involves the unknown homology groups of the original object. This alone is often not sufficient to determine the unknown homology groups, but if one can compare the original object and sub object to well-understood ones via morphisms, then a morphism between the respective long exact sequences is induced, and the five lemma can then be used to determine the unknown homology groups.
See also
- Short five lemmaShort five lemmaIn mathematics, especially homological algebra and other applications of abelian category theory, the short five lemma is a special case of the five lemma....
, a special case of the five lemma for short exact sequences - Snake lemmaSnake lemmaThe snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
, another lemma proved by diagram chasing - Nine lemmaNine lemmaIn mathematics, the nine lemma is a statement about commutative diagrams and exact sequences valid in any abelian category, as well as in the category of groups. It states: ifis a commutative diagram and all columns as well as the two bottom rows are exact, then the top row is exact as well...

