
Fine topology (potential theory)
Encyclopedia
In mathematics
, in the field of potential theory
, the fine topology is a natural topology for setting the study of subharmonic function
s. In the earliest studies of subharmonic functions, only smooth function
s were considered, namely those for which where
where  is the Laplacian. In that case it was natural to consider only the Euclidean
is the Laplacian. In that case it was natural to consider only the Euclidean
topology, but with the advent of upper semi-continuous subharmonic functions introduced by F. Riesz, the fine topology became the more natural tool in many situations.
 is defined to be the
is defined to be the
coarsest
topology
making all subharmonic function
s (equivalently all superharmonic functions) continuous
. Concepts in the fine topology are normally prefixed with the word 'fine' to distinguish them from the corresponding concepts in the usual topology, as for example 'fine neighbourhood' or 'fine continuous'.
to aid in the study of thin sets and was initially considered to be somewhat pathological due to the absence of a number of properties such as local compactness which are so frequently useful in analysis. Subsequent work has shown that the lack of such properties is to a certain extent compensated for by the presence of other slightly less strong properties such as the quasi-Lindelöf property.
In one dimension, that is, on the real line
, the fine topology coincides with the usual topology since in that case the subharmonic functions are precisely the convex function
s which are already continuous in the usual (Euclidean) topology. Thus, the fine topology is of most interest in where
where 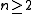 . The fine topology in this case is strictly finer than the usual topology, since there are discontinuous subharmonic functions.
. The fine topology in this case is strictly finer than the usual topology, since there are discontinuous subharmonic functions.
Cartan observed in correspondence with Marcel Brelot that it is equally possible to develop the theory of the fine topology by using the concept of 'thinness'. In this development, a set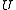 is thin at a point
is thin at a point  if there exists a subharmonic function
if there exists a subharmonic function  defined on a neighbourhood of
defined on a neighbourhood of 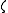 such that
such that

Then, a set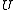 is a fine neighbourhood of
is a fine neighbourhood of  if and only if the complement of
if and only if the complement of 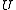 is thin at
is thin at  .
.
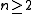 ):
):
The fine topology does at least have a few 'nicer' properties:
The fine topology does not possess the Lindelöf property
but it does have the slightly weaker quasi-Lindelöf property:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, the fine topology is a natural topology for setting the study of subharmonic function
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
s. In the earliest studies of subharmonic functions, only smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s were considered, namely those for which
 where
where  is the Laplacian. In that case it was natural to consider only the Euclidean
is the Laplacian. In that case it was natural to consider only the EuclideanEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
topology, but with the advent of upper semi-continuous subharmonic functions introduced by F. Riesz, the fine topology became the more natural tool in many situations.
Definition
The fine topology on the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
 is defined to be the
is defined to be thecoarsest
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
making all subharmonic function
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
s (equivalently all superharmonic functions) continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Concepts in the fine topology are normally prefixed with the word 'fine' to distinguish them from the corresponding concepts in the usual topology, as for example 'fine neighbourhood' or 'fine continuous'.
Observations
The fine topology was introduced in 1940 by Henri CartanHenri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
to aid in the study of thin sets and was initially considered to be somewhat pathological due to the absence of a number of properties such as local compactness which are so frequently useful in analysis. Subsequent work has shown that the lack of such properties is to a certain extent compensated for by the presence of other slightly less strong properties such as the quasi-Lindelöf property.
In one dimension, that is, on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, the fine topology coincides with the usual topology since in that case the subharmonic functions are precisely the convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s which are already continuous in the usual (Euclidean) topology. Thus, the fine topology is of most interest in
 where
where 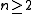 . The fine topology in this case is strictly finer than the usual topology, since there are discontinuous subharmonic functions.
. The fine topology in this case is strictly finer than the usual topology, since there are discontinuous subharmonic functions.Cartan observed in correspondence with Marcel Brelot that it is equally possible to develop the theory of the fine topology by using the concept of 'thinness'. In this development, a set
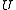 is thin at a point
is thin at a point  if there exists a subharmonic function
if there exists a subharmonic function  defined on a neighbourhood of
defined on a neighbourhood of 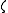 such that
such that
Then, a set
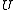 is a fine neighbourhood of
is a fine neighbourhood of  if and only if the complement of
if and only if the complement of 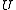 is thin at
is thin at  .
.Properties of the fine topology
The fine topology is in some ways much less tractable than the usual topology in euclidean space, as is evidenced by the following (taking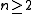 ):
):- A set
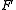 in
in 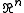 is fine compact if and only if
is fine compact if and only if 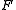 is finite.
is finite. - The fine topology on
 is not locally compact (although it is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is not locally compact (although it is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
). - The fine topology on
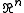 is not first-countableFirst-countable spaceIn topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
is not first-countableFirst-countable spaceIn topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
, second-countableSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
or metrisable.
The fine topology does at least have a few 'nicer' properties:
- The fine topology has the Baire property.
- The fine topology in
 is locally connected.
is locally connected.
The fine topology does not possess the Lindelöf property
Lindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
but it does have the slightly weaker quasi-Lindelöf property:
- An arbitrary union of fine open subsets of
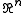 differs by a polar setPolar set (potential theory)In mathematics, in the area of classical potential theory, polar sets are the "negligible sets", similar to the way in which sets of measure zero are the negligible sets in measure theory.- Definition :...
differs by a polar setPolar set (potential theory)In mathematics, in the area of classical potential theory, polar sets are the "negligible sets", similar to the way in which sets of measure zero are the negligible sets in measure theory.- Definition :...
from some countable subunion.

