
Fiber bundle construction theorem
Encyclopedia
In mathematics
, the fiber bundle construction theorem is a theorem
which constructs a fiber bundle
from a given base space, fiber and a suitable set of transition function
s. The theorem also gives conditions under which two such bundles are isomorphic. The theorem is important in the associated bundle
construction where one starts with a given bundle and surgically replaces the fiber with a new space while keeping all other data the same.
s and let G be a topological group
with a continuous left action on F. Given an open cover {Ui} of X and a set of continuous functions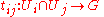
defined on each nonempty overlap, such that the cocycle condition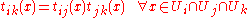
holds, there exists a fiber bundle E → X with fiber F and structure group G that is trivializable over {Ui} with transition functions tij.
Let E′ be another fiber bundle with the same base space, fiber, structure group, and trivializing neighborhoods, but transition functions t′ij. If the action of G on F is faithful, then E′ and E are isomorphic if and only if
there exist functions
such that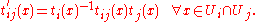
Taking ti to be constant functions to the identity in G, we see that two fiber bundles with the same base, fiber, structure group, trivializing neighborhoods, and transition functions are isomorphic.
A similar theorem holds in the smooth category, where X and Y are smooth manifolds, G is a Lie group
with a smooth left action on Y and the maps tij are all smooth.
. That is, it actually constructs a fiber bundle with the given properties. One starts by taking the disjoint union
of the product spaces Ui × F
and then forms the quotient by the equivalence relation
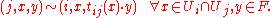
The total space E of the bundle is T/~ and the projection π : E → X is the map which sends the equivalence class of (i, x, y) to x. The local trivializations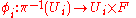
are then defined by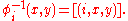
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the fiber bundle construction theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
which constructs a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
from a given base space, fiber and a suitable set of transition function
Transition function
In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
s. The theorem also gives conditions under which two such bundles are isomorphic. The theorem is important in the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
construction where one starts with a given bundle and surgically replaces the fiber with a new space while keeping all other data the same.
Formal statement
Let X and F be topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and let G be a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
with a continuous left action on F. Given an open cover {Ui} of X and a set of continuous functions
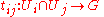
defined on each nonempty overlap, such that the cocycle condition
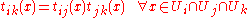
holds, there exists a fiber bundle E → X with fiber F and structure group G that is trivializable over {Ui} with transition functions tij.
Let E′ be another fiber bundle with the same base space, fiber, structure group, and trivializing neighborhoods, but transition functions t′ij. If the action of G on F is faithful, then E′ and E are isomorphic if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exist functions

such that
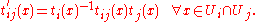
Taking ti to be constant functions to the identity in G, we see that two fiber bundles with the same base, fiber, structure group, trivializing neighborhoods, and transition functions are isomorphic.
A similar theorem holds in the smooth category, where X and Y are smooth manifolds, G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
with a smooth left action on Y and the maps tij are all smooth.
Construction
The proof of the theorem is constructiveConstructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
. That is, it actually constructs a fiber bundle with the given properties. One starts by taking the disjoint union
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
of the product spaces Ui × F

and then forms the quotient by the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
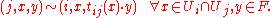
The total space E of the bundle is T/~ and the projection π : E → X is the map which sends the equivalence class of (i, x, y) to x. The local trivializations
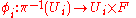
are then defined by
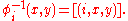
Associated bundle
Let E → X a fiber bundle with fiber F and structure group G, and let F′ be another left G-space. One can form an associated bundle E′ → X a with fiber F′ and structure group G by taking any local trivialization of E and replacing F by F′ in the construction theorem. If one takes F′ to be G with the action of left multiplication then one obtains the associated principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
.

