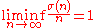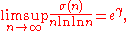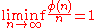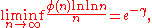Extremal orders of an arithmetic function
Encyclopedia
In mathematics
, in number theory
, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function
. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and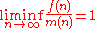
we say that m is a minimal order for f. Similarly if M(n) is a non-decreasing function that is ultimately positive and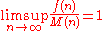
we say that M is a maximal order for f.
The subject was first studied systematically by Ramanujan
starting in 1915.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and
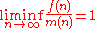
we say that m is a minimal order for f. Similarly if M(n) is a non-decreasing function that is ultimately positive and
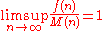
we say that M is a maximal order for f.
The subject was first studied systematically by Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
starting in 1915.
Examples
- For the sum-of-divisors function σ(n) we have the trivial result
-
- because always σ(n) ≥ n and for primes σ(p) = p + 1. We also have
- proved by GronwallThomas Hakon GrönwallThomas Hakon Grönwall or Thomas Hakon Gronwall was a Swedish mathematician. He studied at the University College of Stockholm and Uppsala University and completed his Ph.D. at Uppsala in 1898. Grönwall worked for about a year as a civil engineer in Germany before he immigrated to the United...
in 1913. Therefore n is a minimal order and e−γ n ln ln n is a maximal order for σ(n).- For the Euler totient φ(n) we have the trivial result
- because always φ(n) ≤ n and for primes φ(p) = p − 1. We also have
- proved by LandauEdmund LandauEdmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
in 1903.- For the number of divisors function d(n) we have the trivial lower bound 2 ≤ d(n), in which equality occurs when n is prime, so 2 is a minimal order. For ln d(n) we have a maximal order ln 2 ln n / ln ln n, proved by Wigert in 1907.
- For the number of distinct prime factors ω(n) we have a trivial lower bound 1 ≤ ω(n), in which equality occurs when n is prime. A maximal order for ω(n) is ln n / ln ln n.
- For the number of prime factors counted with multiplicity Ω(n) we have a trivial lower bound 1 ≤ Ω(n), in which equality occurs when n is prime. A maximal order for Ω(n) is ln n / ln 2.
See also
- Average order of an arithmetic functionAverage order of an arithmetic functionIn number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".Let f be an arithmetic function...
- Normal order of an arithmetic functionNormal order of an arithmetic functionIn number theory, the normal order of an arithmetic function is some simpler or better-understood function which "usually" takes the same or closely approximate values.Let ƒ be a function on the natural numbers...