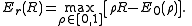Error exponent
Encyclopedia
In information theory
, the error exponent of a channel code
or source code
over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder
drops as e–nα, where n is the block length, the error exponent is α. Many of the information-theoretic
theorems are of asymptotic nature, for example, the channel coding theorem
states that for any rate less than the channel capacity, the probability of the error of the channel code can made to go to zero as the block length goes to infinity. In practical situations, there are limitations to the delay of the communication and the block length of the code cannot be taken to go to infinity. Therefore it is important to study how the probability of error drops as the block length go to infinity.
states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of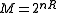 messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass function
messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass function
Q. At the decoding end, ML decoding is done.
Given that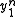 is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is:
is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is:
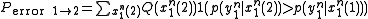
The function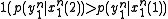 has upper bound
has upper bound

for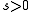 Thus,
Thus,
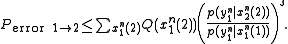
Since there are a total of M messages, the Probability that X(1) is confused with any other message is M times the above expression. Since each entry in the codebook is i.i.d., the notation of X(2) can be replaced simply by X. Using the Hokey union bound, the probability of confusing X(1) with any message is bounded by:
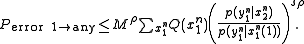
Averaging over all combinations of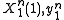 :
:
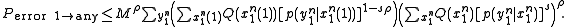
Choosing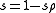 and combining the two sums over
and combining the two sums over 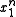 in the above formula:
in the above formula:
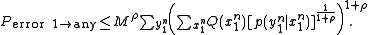
Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
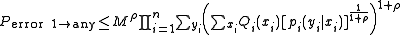
Using the fact that each element of codeword is identically distributed and thus stationary:

Replacing M by 2nR and defining
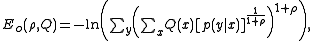
probability of error becomes
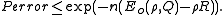
Q and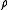 should be chosen so that the bound is tighest. Thus, the error exponent can be defined as
should be chosen so that the bound is tighest. Thus, the error exponent can be defined as

theorem states that for any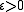 and any discrete-time i.i.d. source such as
and any discrete-time i.i.d. source such as  and for any rate less than the entropy
and for any rate less than the entropy
of the source, there is large enough and an encoder that takes
and an encoder that takes  i.i.d. repetition of the source,
i.i.d. repetition of the source,  , and maps it to
, and maps it to  binary bits such that the source symbols
binary bits such that the source symbols 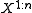 are recoverable from the binary bits with probability at least
are recoverable from the binary bits with probability at least  .
.
Let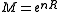 be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message
be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message 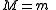 is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence
is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence 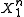 that maximizes
that maximizes 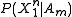 , where
, where  denotes the event that message
denotes the event that message 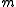 was transmitted. This rule is equivalent to finding the source sequence
was transmitted. This rule is equivalent to finding the source sequence 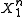 among the set of source sequences that map to message
among the set of source sequences that map to message 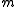 that maximizes
that maximizes 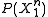 . This reduction follows from the fact that the messages were assigned randomly and independently of everything else.
. This reduction follows from the fact that the messages were assigned randomly and independently of everything else.
Thus, as an example of when an error occurs, supposed that the source sequence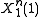 was mapped to message
was mapped to message 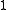 as was the source sequence
as was the source sequence 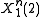 . If
. If 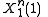 was generated at the source, but
was generated at the source, but 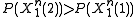 then an error occurs.
then an error occurs.
Let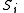 denote the event that the source sequence
denote the event that the source sequence 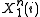 was generated at the source, so that
was generated at the source, so that  Then the probability of error can be broken down as
Then the probability of error can be broken down as 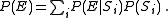 Thus, attention can be focused on finding an upper bound to the
Thus, attention can be focused on finding an upper bound to the 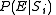 .
.
Let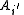 denote the event that the source sequence
denote the event that the source sequence 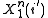 was mapped to the same message as the source sequence
was mapped to the same message as the source sequence 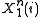 and that
and that 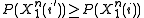 . Thus, letting
. Thus, letting 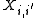 denote the event that the two source sequences
denote the event that the two source sequences 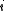 and
and  map to the same message, we have that
map to the same message, we have that
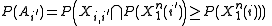
and using the fact that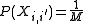 and is independent of everything else have that
and is independent of everything else have that
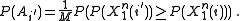
A simple upper bound for the term on the left can be established as

for some arbitrary real number This upper bound can be verified by noting that
This upper bound can be verified by noting that  either equals
either equals  or
or  because the probabilities of a given input sequence are completely deterministic. Thus, if
because the probabilities of a given input sequence are completely deterministic. Thus, if 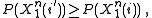 then
then 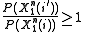 so that the inequality holds in that case. The inequality holds in the other case as well because
so that the inequality holds in that case. The inequality holds in the other case as well because

for all possible source strings. Thus, combining everything and introducing some , have that
, have that
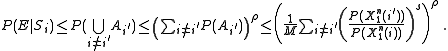
Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for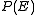 have that:
have that:
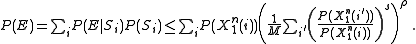
Where the sum can now be taken over all because that will only increase the bound. Ultimately yielding that
because that will only increase the bound. Ultimately yielding that
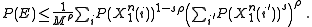
Now for simplicity let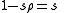 so that
so that 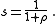 Substituting this new value of
Substituting this new value of 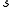 into the above bound on the probability of error and using the fact that
into the above bound on the probability of error and using the fact that 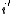 is just a dummy variable in the sum gives the following as an upper bound on the probability of error:
is just a dummy variable in the sum gives the following as an upper bound on the probability of error:
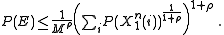
 and each of the components of
and each of the components of 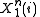 are independent. Thus, simplifying the above equation yields
are independent. Thus, simplifying the above equation yields
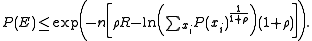
The term in the exponent should be maximized over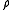 in order to achieve the tightest upper bound on the probability of error.
in order to achieve the tightest upper bound on the probability of error.
Letting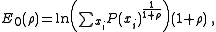 see that the error exponent for the source coding case is:
see that the error exponent for the source coding case is:
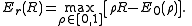
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the error exponent of a channel code
Channel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
or source code
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder
Decoder
A decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
drops as e–nα, where n is the block length, the error exponent is α. Many of the information-theoretic
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
theorems are of asymptotic nature, for example, the channel coding theorem
Noisy channel coding theorem
In information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
states that for any rate less than the channel capacity, the probability of the error of the channel code can made to go to zero as the block length goes to infinity. In practical situations, there are limitations to the delay of the communication and the block length of the code cannot be taken to go to infinity. Therefore it is important to study how the probability of error drops as the block length go to infinity.
For time-invariant DMC channels
The channel coding theoremNoisy channel coding theorem
In information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
states that for any ε > 0 and for any rate less than the channel capacity, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε > 0 for sufficiently long message block X. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.
Assuming a channel coding setup as follows: the channel can transmit any of
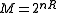 messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass function
messages, by transmitting the corresponding codeword (which is of length n). Each component in the codebook is drawn i.i.d. according to some probability distribution with probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
Q. At the decoding end, ML decoding is done.
Given that
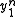 is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is:
is received, X(1) or first message is transmitted, the probability that X(1) is incorrectly detected as X(2) is: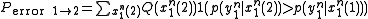
The function
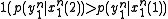 has upper bound
has upper bound
for
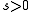 Thus,
Thus,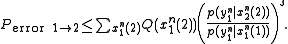
Since there are a total of M messages, the Probability that X(1) is confused with any other message is M times the above expression. Since each entry in the codebook is i.i.d., the notation of X(2) can be replaced simply by X. Using the Hokey union bound, the probability of confusing X(1) with any message is bounded by:
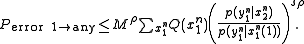
Averaging over all combinations of
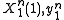 :
: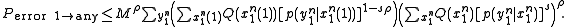
Choosing
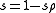 and combining the two sums over
and combining the two sums over 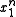 in the above formula:
in the above formula: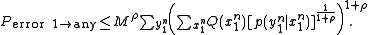
Using the independence nature of the elements of the codeword, and the discrete memoryless nature of the channel:
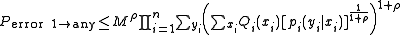
Using the fact that each element of codeword is identically distributed and thus stationary:

Replacing M by 2nR and defining
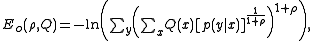
probability of error becomes
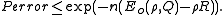
Q and
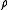 should be chosen so that the bound is tighest. Thus, the error exponent can be defined as
should be chosen so that the bound is tighest. Thus, the error exponent can be defined as
For time invariant discrete memoryless sources
The source codingSource coding
In information theory, Shannon's source coding theorem establishes the limits to possible data compression, and the operational meaning of the Shannon entropy....
theorem states that for any
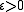 and any discrete-time i.i.d. source such as
and any discrete-time i.i.d. source such as  and for any rate less than the entropy
and for any rate less than the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the source, there is large enough
 and an encoder that takes
and an encoder that takes  i.i.d. repetition of the source,
i.i.d. repetition of the source,  , and maps it to
, and maps it to  binary bits such that the source symbols
binary bits such that the source symbols 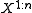 are recoverable from the binary bits with probability at least
are recoverable from the binary bits with probability at least  .
.Let
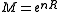 be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message
be the total number of possible messages. Next map each of the possible source output sequences to one of the messages randomly using a uniform distribution and independently from everything else. When a source is generated the corresponding message 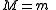 is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence
is then transmitted to the destination. The message gets decoded to one of the possible source strings. In order to minimize the probability of error the decoder will decode to the source sequence 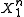 that maximizes
that maximizes 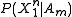 , where
, where  denotes the event that message
denotes the event that message 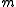 was transmitted. This rule is equivalent to finding the source sequence
was transmitted. This rule is equivalent to finding the source sequence 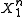 among the set of source sequences that map to message
among the set of source sequences that map to message 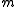 that maximizes
that maximizes 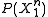 . This reduction follows from the fact that the messages were assigned randomly and independently of everything else.
. This reduction follows from the fact that the messages were assigned randomly and independently of everything else.Thus, as an example of when an error occurs, supposed that the source sequence
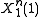 was mapped to message
was mapped to message 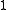 as was the source sequence
as was the source sequence 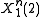 . If
. If 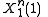 was generated at the source, but
was generated at the source, but 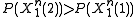 then an error occurs.
then an error occurs.Let
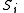 denote the event that the source sequence
denote the event that the source sequence 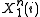 was generated at the source, so that
was generated at the source, so that  Then the probability of error can be broken down as
Then the probability of error can be broken down as 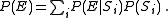 Thus, attention can be focused on finding an upper bound to the
Thus, attention can be focused on finding an upper bound to the 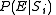 .
.Let
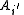 denote the event that the source sequence
denote the event that the source sequence 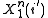 was mapped to the same message as the source sequence
was mapped to the same message as the source sequence 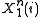 and that
and that 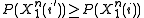 . Thus, letting
. Thus, letting 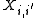 denote the event that the two source sequences
denote the event that the two source sequences 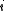 and
and  map to the same message, we have that
map to the same message, we have that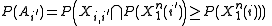
and using the fact that
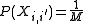 and is independent of everything else have that
and is independent of everything else have that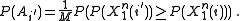
A simple upper bound for the term on the left can be established as

for some arbitrary real number
 This upper bound can be verified by noting that
This upper bound can be verified by noting that  either equals
either equals  or
or  because the probabilities of a given input sequence are completely deterministic. Thus, if
because the probabilities of a given input sequence are completely deterministic. Thus, if 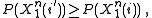 then
then 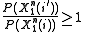 so that the inequality holds in that case. The inequality holds in the other case as well because
so that the inequality holds in that case. The inequality holds in the other case as well because
for all possible source strings. Thus, combining everything and introducing some
 , have that
, have that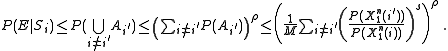
Where the inequalities follow from a variation on the Union Bound. Finally applying this upper bound to the summation for
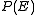 have that:
have that: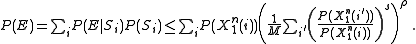
Where the sum can now be taken over all
 because that will only increase the bound. Ultimately yielding that
because that will only increase the bound. Ultimately yielding that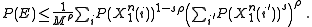
Now for simplicity let
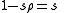 so that
so that 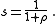 Substituting this new value of
Substituting this new value of 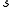 into the above bound on the probability of error and using the fact that
into the above bound on the probability of error and using the fact that 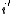 is just a dummy variable in the sum gives the following as an upper bound on the probability of error:
is just a dummy variable in the sum gives the following as an upper bound on the probability of error: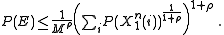
 and each of the components of
and each of the components of 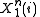 are independent. Thus, simplifying the above equation yields
are independent. Thus, simplifying the above equation yields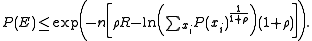
The term in the exponent should be maximized over
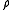 in order to achieve the tightest upper bound on the probability of error.
in order to achieve the tightest upper bound on the probability of error.Letting
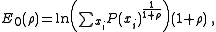 see that the error exponent for the source coding case is:
see that the error exponent for the source coding case is: