Channel capacity
Encyclopedia
In electrical engineering
, computer science
and information theory
, channel capacity is the tightest upper bound on the amount of information
that can be reliably transmitted over a communications channel
. By the noisy-channel coding theorem, the channel capacity of a given channel
is the limiting information rate (in units of information
per unit time) that can be achieved with arbitrarily small error probability.
Information theory
, developed by Claude E. Shannon during World War II
, defines the notion of channel capacity and provides a mathematical model by which one can compute it. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information
between the input and output of the channel, where the maximization is with respect to the input distribution.
Let X represent the space of signals that can be transmitted, and Y the space of signals received, during a block of time over the channel. Let
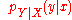
be the conditional distribution
function of Y given X. Treating the channel as a known statistic system,
is an inherent fixed property of the communications channel (representing the nature of the noise in it). Then the joint distribution
of X and Y is completely determined by the channel and by the choice of
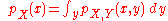
the marginal distribution
of signals we choose to send over the channel. The joint distribution can be recovered by using the identity
Under these constraints, next maximize the amount of information, or the message, that one can communicate over the channel. The appropriate measure for this is the mutual information
, and this maximum mutual information is called the channel capacity and is given by
(AWGN) channel with B Hz bandwidth and signal-to-noise ratio
S/N is the Shannon–Hartley theorem
:
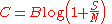
C is measured in bits per second if the logarithm
is taken in base 2, or nats per second
if the natural logarithm
is used, assuming B is in hertz
; the signal and noise powers S and N are measured in watts or volts2, so the signal-to-noise ratio here is expressed as a power ratio, not in decibel
s (dB); since figures are often cited in dB, a conversion may be needed. For example, 30 dB is a power ratio of
.
.
[W] and the noise power spectral density is 
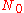[W/Hz], the AWGN channel capacity is
[bits/Hz],
where
is the received signal-to-noise ratio (SNR).
When the SNR is large (SNR >> 0 dB), the capacity
is logarithmic in power and approximately linear in bandwidth. This is called the bandwidth-limited regime.
When the SNR is small (SNR << 0 dB), the capacity
is linear in power but insensitive to bandwidth. This is called the power-limited regime.
The bandwidth-limited regime and power-limited regime are illustrated in the figure.
channel is given by so-called waterfilling power allocation,
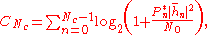
where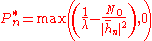
and 
is the gain of subchannel 
, with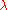 
chosen to meet the power constraint.
, where the coherence time is greater than the latency requirement, there is no definite capacity as the maximum rate of reliable communications supported by the channel,
, depends on the random channel gain 
. If the transmitter encodes data at rate 
[bits/s/Hz], there is a certain probability that the decoding error probability cannot be made arbitrarily small,
,
in which case the system is said to be in outage. With a non-zero probability that the channel is in deep fade, the capacity of the slow-fading channel in strict sense is zero. However, it is possible to determine the largest value of
such that the outage probability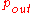 
is less than 
. This value is known as the 
-outage capacity.
, where the latency requirement is greater than the coherence time and the codeword length spans many coherence periods, one can average over many independent channel fades by coding over a large number of coherence time intervals. Thus, it is possible to achieve a reliable rate of communication of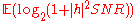
[bits/s/Hz] and it is meaningful to speak of this value as the capacity of the fast-fading channel.
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, channel capacity is the tightest upper bound on the amount of information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
that can be reliably transmitted over a communications channel
Channel (communications)
In telecommunications and computer networking, a communication channel, or channel, refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel...
. By the noisy-channel coding theorem, the channel capacity of a given channel
Channel (communications)
In telecommunications and computer networking, a communication channel, or channel, refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel...
is the limiting information rate (in units of information
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
per unit time) that can be achieved with arbitrarily small error probability.
Information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, developed by Claude E. Shannon during World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
, defines the notion of channel capacity and provides a mathematical model by which one can compute it. The key result states that the capacity of the channel, as defined above, is given by the maximum of the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between the input and output of the channel, where the maximization is with respect to the input distribution.
Formal definition
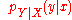
be the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
function of Y given X. Treating the channel as a known statistic system,
is an inherent fixed property of the communications channel (representing the nature of the noise in it). Then the joint distributionof X and Y is completely determined by the channel and by the choice of
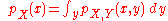
the marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
of signals we choose to send over the channel. The joint distribution can be recovered by using the identity
Under these constraints, next maximize the amount of information, or the message, that one can communicate over the channel. The appropriate measure for this is the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, and this maximum mutual information is called the channel capacity and is given byNoisy-channel coding theorem
The noisy-channel coding theorem states that for any ε > 0 and for any rate R less than the channel capacity C, there is an encoding and decoding scheme that can be used to ensure that the probability of block error is less than ε for a sufficiently long code. Also, for any rate greater than the channel capacity, the probability of block error at the receiver goes to one as the block length goes to infinity.Example application
An application of the channel capacity concept to an additive white Gaussian noiseAdditive white Gaussian noise
Additive white Gaussian noise is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference,...
(AWGN) channel with B Hz bandwidth and signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
S/N is the Shannon–Hartley theorem
Shannon–Hartley theorem
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy channel coding theorem to the archetypal case of a continuous-time...
:
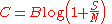
C is measured in bits per second if the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is taken in base 2, or nats per second
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
if the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
is used, assuming B is in hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
; the signal and noise powers S and N are measured in watts or volts2, so the signal-to-noise ratio here is expressed as a power ratio, not in decibel
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
s (dB); since figures are often cited in dB, a conversion may be needed. For example, 30 dB is a power ratio of
.Channel capacity in wireless communications
This section focuses on the single-antenna, point-to-point scenario. For channel capacity in systems with multiple antennas, see the article on MIMOMIMO
In radio, multiple-input and multiple-output, or MIMO , is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology...
.
AWGN channel
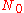If the average received power is [W] and the noise power spectral density is [W/Hz], the AWGN channel capacity is [bits/Hz],where
is the received signal-to-noise ratio (SNR).When the SNR is large (SNR >> 0 dB), the capacity
is logarithmic in power and approximately linear in bandwidth. This is called the bandwidth-limited regime.When the SNR is small (SNR << 0 dB), the capacity
is linear in power but insensitive to bandwidth. This is called the power-limited regime.The bandwidth-limited regime and power-limited regime are illustrated in the figure.
Frequency-selective channel
The capacity of the frequency-selectiveFading
In wireless communications, fading is deviation of the attenuation that a carrier-modulated telecommunication signal experiences over certain propagation media. The fading may vary with time, geographical position and/or radio frequency, and is often modelled as a random process. A fading channel...
channel is given by so-called waterfilling power allocation,
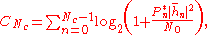
where
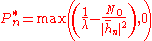and is the gain of subchannel , with 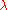chosen to meet the power constraint.Slow-fading channel
In a slow-fading channelFading
In wireless communications, fading is deviation of the attenuation that a carrier-modulated telecommunication signal experiences over certain propagation media. The fading may vary with time, geographical position and/or radio frequency, and is often modelled as a random process. A fading channel...
, where the coherence time is greater than the latency requirement, there is no definite capacity as the maximum rate of reliable communications supported by the channel,
, depends on the random channel gain . If the transmitter encodes data at rate [bits/s/Hz], there is a certain probability that the decoding error probability cannot be made arbitrarily small,,in which case the system is said to be in outage. With a non-zero probability that the channel is in deep fade, the capacity of the slow-fading channel in strict sense is zero. However, it is possible to determine the largest value of
such that the outage probability 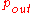is less than . This value is known as the -outage capacity.Fast-fading channel
In a fast-fading channelFading
In wireless communications, fading is deviation of the attenuation that a carrier-modulated telecommunication signal experiences over certain propagation media. The fading may vary with time, geographical position and/or radio frequency, and is often modelled as a random process. A fading channel...
, where the latency requirement is greater than the coherence time and the codeword length spans many coherence periods, one can average over many independent channel fades by coding over a large number of coherence time intervals. Thus, it is possible to achieve a reliable rate of communication of
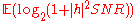[bits/s/Hz] and it is meaningful to speak of this value as the capacity of the fast-fading channel.See also
- Bandwidth (computing)Bandwidth (computing)In computer networking and computer science, bandwidth, network bandwidth, data bandwidth, or digital bandwidth is a measure of available or consumed data communication resources expressed in bits/second or multiples of it .Note that in textbooks on wireless communications, modem data transmission,...
- Bandwidth (signal processing)
- Bit rateBit rateIn telecommunications and computing, bit rate is the number of bits that are conveyed or processed per unit of time....
- Code rateCode rateIn telecommunication and information theory, the code rate of a forward error correction code is the proportion of the data-stream that is useful...
- Error exponentError exponentIn information theory, the error exponent of a channel code or source code over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder drops as e–nα, where n is the block length, the error exponent is α...
- Nyquist rateNyquist rateIn signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel...
- NegentropyNegentropyThe negentropy, also negative entropy or syntropy, of a living system is the entropy that it exports to keep its own entropy low; it lies at the intersection of entropy and life...
- RedundancyRedundancy (information theory)Redundancy in information theory is the number of bits used to transmit a message minus the number of bits of actual information in the message. Informally, it is the amount of wasted "space" used to transmit certain data...
- SenderSenderA sender was a circuit in a 20th century electromechanical telephone exchange which sent telephone numbers and other information to another exchange. In some American exchange designs, for example 1XB switch the same term was also used to refer to the circuit that received this information...
, EncoderEncoderAn encoder is a device, circuit, transducer, software program, algorithm or person that converts information from one format or code to another, for the purposes of standardization, speed, secrecy, security, or saving space by shrinking size.-Media:...
, DecoderDecoderA decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
, ReceiverReceiver (Information Theory)The receiver in information theory is the receiving end of a communication channel. It receives decoded messages/information from the sender, who first encoded them. Sometimes the receiver is modeled so as to include the decoder. Real-world receivers like radio receivers or telephones can not be... - Shannon–Hartley theoremShannon–Hartley theoremIn information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy channel coding theorem to the archetypal case of a continuous-time...
- Spectral efficiencySpectral efficiencySpectral efficiency, spectrum efficiency or bandwidth efficiency refers to the information rate that can be transmitted over a given bandwidth in a specific communication system...
- ThroughputThroughputIn communication networks, such as Ethernet or packet radio, throughput or network throughput is the average rate of successful message delivery over a communication channel. This data may be delivered over a physical or logical link, or pass through a certain network node...