
Eilenberg–Mazur swindle
Encyclopedia
In mathematics
, the Eilenberg–Mazur swindle, named after Samuel Eilenberg
and Barry Mazur
, is a method of proof that involves paradoxical properties of infinite sums. In geometric topology
it was introduced by and is often called the Mazur swindle. In algebra it was introduced by Samuel Eilenberg and is known as the Eilenberg swindle or Eilenberg telescope (see telescoping sum).
The Eilenberg–Mazur swindle is similar to the following well known joke "proof" that 1 = 0:
This "proof" is not valid as a claim about real numbers because Grandi's series 1 − 1 + 1 − 1 + ... does not converge, but the analogous argument can be used in some contexts where there is some sort of "addition" defined on some objects for which infinite sums do make sense,
to show that if A + B = 0 then A = B = 0.
of knots or manifolds.
Example : A typical application of the Mazur swindle in geometric topology is the proof that the sum of two non-trivial knot
s A and B is non-trivial. For knots it is possible to take infinite sums by making the knots smaller and smaller, so if A + B is trivial then
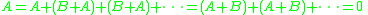
so A is trivial (and B by a similar argument). The infinite sum of knots is usually a wild knot
, not a tame knot.
See for more geometric examples.
Example: The oriented n-manifolds have an addition operation given by connected sum, with 0 the n-sphere. If A + B is the n-sphere, then A + B + A + B + ... is Euclidean space so the Mazur swindle shows that the connected sum of A and Euclidean space is Euclidean space, which shows that A is the 1-point compactification of Euclidean space and therefore A is homeomorphic to the n-sphere. (This does not show in the case of smooth manifolds that A is diffeomorphic to the n-sphere, and in most dimensions at least 7 there are examples of exotic sphere
s A with inverses that are not diffeomorphic to the standard n-sphere.)
over a ring
.
Example: A typical application of the Eilenberg swindle in algebra is the proof that if A is a projective module
over a ring R then there is a free module
with A + F = F. To see this, choose a module B such that A + B is free, which can be done as A is projective, and put
so that
Example: Finitely generated free modules over commutative rings R have a well-defined natural number as their dimension which is additive under direct sums, and are isomorphic if and only if they have the same dimension.
This is false for some noncommutative rings, and a counterexample can be constructed using the Eilenberg swindle as follows. Let X be an abelian group such that X = X + X (for example the direct sum of an infinite number of copies of an abelian group), and let R be the ring of endomorphisms of X. Then the left R-module R is isomorphic to the left R-module R + R.
Example: If A and B are any groups then the Eilenberg swindle can be used to construct a ring R such that the group rings R[A] and R[B] are isomorphic rings: take R to be the group ring of A + B + A + B + ...
uses a similar idea. If there are injections of sets from X to Y and from Y to X, this means that formally we have X=Y+A and Y=X+B for some sets A and B, where + means disjoint union and = means there is a bijection between two sets. Then
and
for some set Z, which shows that X=Y.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Eilenberg–Mazur swindle, named after Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
, is a method of proof that involves paradoxical properties of infinite sums. In geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
it was introduced by and is often called the Mazur swindle. In algebra it was introduced by Samuel Eilenberg and is known as the Eilenberg swindle or Eilenberg telescope (see telescoping sum).
The Eilenberg–Mazur swindle is similar to the following well known joke "proof" that 1 = 0:
- 1 = 1 + (−1 + 1) + (−1 + 1) + ... = 1 − 1 + 1 − 1 + ... = (1 − 1) + (1 − 1) + ... = 0
This "proof" is not valid as a claim about real numbers because Grandi's series 1 − 1 + 1 − 1 + ... does not converge, but the analogous argument can be used in some contexts where there is some sort of "addition" defined on some objects for which infinite sums do make sense,
to show that if A + B = 0 then A = B = 0.
Mazur swindle
In geometric topology the addition used in the swindle is usually the connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of knots or manifolds.
Example : A typical application of the Mazur swindle in geometric topology is the proof that the sum of two non-trivial knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
s A and B is non-trivial. For knots it is possible to take infinite sums by making the knots smaller and smaller, so if A + B is trivial then
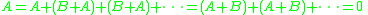
so A is trivial (and B by a similar argument). The infinite sum of knots is usually a wild knot
Wild knot
In the mathematical theory of knots, a knot is tame if it can be "thickened up", that is, if there exists an extension to an embedding of the solid torus S 1 × D 2 into the 3-sphere. A knot is tame if and only if it can be represented as a finite closed polygonal chain...
, not a tame knot.
See for more geometric examples.
Example: The oriented n-manifolds have an addition operation given by connected sum, with 0 the n-sphere. If A + B is the n-sphere, then A + B + A + B + ... is Euclidean space so the Mazur swindle shows that the connected sum of A and Euclidean space is Euclidean space, which shows that A is the 1-point compactification of Euclidean space and therefore A is homeomorphic to the n-sphere. (This does not show in the case of smooth manifolds that A is diffeomorphic to the n-sphere, and in most dimensions at least 7 there are examples of exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s A with inverses that are not diffeomorphic to the standard n-sphere.)
Eilenberg swindle
In algebra the addition used in the swindle is usually the direct sum of modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
Example: A typical application of the Eilenberg swindle in algebra is the proof that if A is a projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
over a ring R then there is a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
with A + F = F. To see this, choose a module B such that A + B is free, which can be done as A is projective, and put
- F = B + A + B + A + B + ....
so that
- A + F = A + (B + A) + (B + A) + ... = (A + B) + (A + B) + ... = F.
Example: Finitely generated free modules over commutative rings R have a well-defined natural number as their dimension which is additive under direct sums, and are isomorphic if and only if they have the same dimension.
This is false for some noncommutative rings, and a counterexample can be constructed using the Eilenberg swindle as follows. Let X be an abelian group such that X = X + X (for example the direct sum of an infinite number of copies of an abelian group), and let R be the ring of endomorphisms of X. Then the left R-module R is isomorphic to the left R-module R + R.
Example: If A and B are any groups then the Eilenberg swindle can be used to construct a ring R such that the group rings R[A] and R[B] are isomorphic rings: take R to be the group ring of A + B + A + B + ...
Other examples
The proof of the Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theorem
In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
uses a similar idea. If there are injections of sets from X to Y and from Y to X, this means that formally we have X=Y+A and Y=X+B for some sets A and B, where + means disjoint union and = means there is a bijection between two sets. Then
- X=A+B+A+B+...+Z
and
- Y=B+A+B+A+...+Z
for some set Z, which shows that X=Y.
External links
- Talk by John Stallings on Mazur's swindle in topology
- Exposition by Terence Tao on Mazur's swindle in topology

