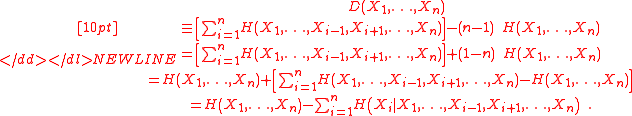Dual total correlation
Encyclopedia
In information theory
, dual total correlation (Han 1978) or excess entropy (Olbrich 2008) is one of the two known non-negative generalizations of mutual information
. While total correlation
is bounded by the sum entropies of the n elements, the dual total correlation is bounded by the joint-entropy of the n elements. Although well behaved, dual total correlation has received much less attention than the total correlation. A measure known as "TSE-complexity" defines a continuum between the total correlation and dual total correlation (Ay 2001).
s , the dual total correlation
, the dual total correlation  is given by
is given by

where is the joint entropy of the variable set
is the joint entropy of the variable set  and
and 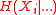 is the conditional entropy
is the conditional entropy
of variable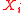 , given the rest.
, given the rest.
 ,
,
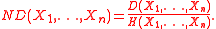
 .
.
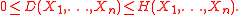
Secondly, Dual total correlation has a close relationship with total correlation, . In particular,
. In particular,
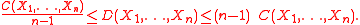
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, dual total correlation (Han 1978) or excess entropy (Olbrich 2008) is one of the two known non-negative generalizations of mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
. While total correlation
Total correlation
In probability theory and in particular in information theory, total correlation is one of several generalizations of the mutual information. It is also known as the multivariate constraint or multiinformation...
is bounded by the sum entropies of the n elements, the dual total correlation is bounded by the joint-entropy of the n elements. Although well behaved, dual total correlation has received much less attention than the total correlation. A measure known as "TSE-complexity" defines a continuum between the total correlation and dual total correlation (Ay 2001).
Definition
For a set of n random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s
 , the dual total correlation
, the dual total correlation  is given by
is given by
where
 is the joint entropy of the variable set
is the joint entropy of the variable set  and
and 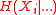 is the conditional entropy
is the conditional entropyConditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
of variable
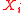 , given the rest.
, given the rest.Normalized
The dual total correlation normalized between [0,1] is simply the dual total correlation divided by its maximum value ,
,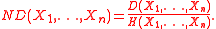
Bounds
Dual total correlation is non-negative and bounded above by the joint entropy .
.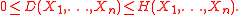
Secondly, Dual total correlation has a close relationship with total correlation,
 . In particular,
. In particular,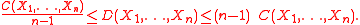
History
Han (1978) originally defined the dual total correlation as,-
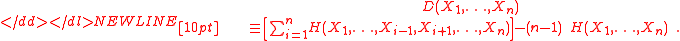
However Abdallah and Plumbley (2010) showed its equivalence to the easier-to-understand form of the joint entropy minus the sum of conditional entropies via the following:
-