Discrete Poisson equation
Encyclopedia
In mathematics
, the discrete Poisson equation is the finite difference
analog of the Poisson equation. In it, the discrete Laplace operator
takes the place of the Laplace operator
. The discrete Poisson equation is frequently used in numerical analysis
as a stand-in for the continuous Poisson equation, although it is also studied in its own right as a topic in discrete mathematics
.
numerical method to discretize
the 2 dimensional Poisson equation (assuming a uniform spatial discretization,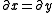
) on an m × n grid gives the following formula:
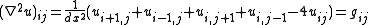
where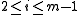
and 
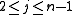. The preferred arrangement of the solution vector is to use natural ordering which, prior to removing boundary elements, would look like:
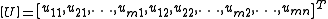
This will result in an mn × mn linear system:
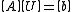
where
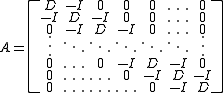
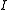is the m × m identity matrix
, and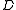
, also m × m, is given by:
For each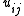
equation, the columns of 
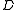correspond to the 
components:
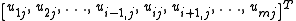
while the columns of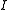
to the left and right of 
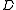correspond to the 
components:
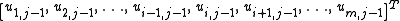
and
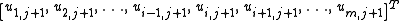
respectively.
From the above, it can be inferred that there are
block columns of 
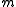in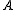 
. It is important to note that prescribed values of 
(usually lying on the boundary) would have their corresponding elements removed from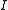 
and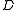 
. For the common case that all the nodes on the boundary are set, we have 
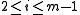and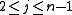 
, and the system would have the dimensions (m − 2)(n − 2) × (m − 2)(n − 2), where 
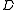and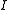 
would have dimensions (m − 2) × (m − 2).
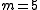and 
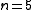) grid with all the boundary nodes prescribed,
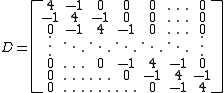
the system would look like:
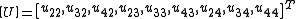
with
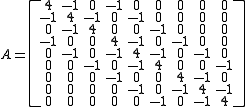
and
As can be seen, the boundary
's are brought to the right-hand-side
of the equation. The entire system is 9 × 9 while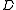
and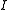 
are 3 × 3 and given by:
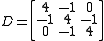
and
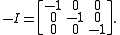
is block tridiagonal and sparse, many methods of solution
have been developed to optimally solve this linear system for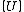
.
Among the methods are a generalized Thomas algorithm,
cyclic reduction, successive overrelaxation, and Fourier transform
s. A theoretically optimal
solution can be computed using multigrid methods.
, for the solution of an incompressible flow problem, the incompressibility condition acts as a constraint for the pressure. There is no explicit form available for pressure in this case due to a strong coupling of the velocity and pressure fields. In this condition, by taking the divergence of all terms in the momentum equation, one obtains the pressure poisson equation. For an incompressible flow this constraint is given by: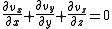
where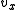
is the velocity in the 
direction, 
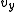is
velocity in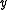
and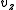 
is the velocity in the 
direction. Taking divergence of the momentum equation and using the incompressibility constraint, the pressure poisson equation is formed given by: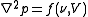
where
is the kinematic viscosity of the fluid and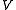 
is the velocity vector.
The discrete Poisson's equation arises in the theory of
Markov chain
s. It appears as the relative value function for the dynamic programming equation in a Markov decision process
, and as the control variate
for application in simulation variance reduction.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the discrete Poisson equation is the finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
analog of the Poisson equation. In it, the discrete Laplace operator
Discrete Laplace operator
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
takes the place of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. The discrete Poisson equation is frequently used in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
as a stand-in for the continuous Poisson equation, although it is also studied in its own right as a topic in discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
.
On a two-dimensional rectangular grid
Using the finite differenceFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
numerical method to discretize
the 2 dimensional Poisson equation (assuming a uniform spatial discretization,
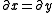) on an m × n grid gives the following formula: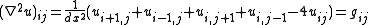where
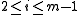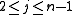and . The preferred arrangement of the solution vector is to use natural ordering which, prior to removing boundary elements, would look like: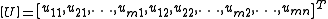This will result in an mn × mn linear system:
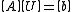
where
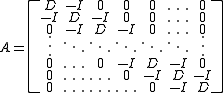
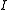is the m × m identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and
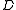, also m × m, is given by:For each
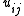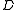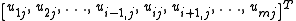
equation, the columns of correspond to the components:while the columns of
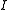to the left and right of 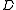correspond to the components: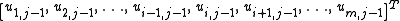and
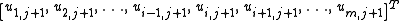
respectively.
From the above, it can be inferred that there are
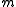block columns of in 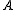. It is important to note that prescribed values of (usually lying on the boundary) would have their corresponding elements removed from 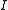and 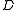. For the common case that all the nodes on the boundary are set, we have 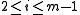and 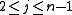, and the system would have the dimensions (m − 2)(n − 2) × (m − 2)(n − 2), where 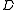and 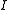would have dimensions (m − 2) × (m − 2).Example
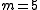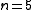For a 5×5 ( and ) grid with all the boundary nodes prescribed,the system would look like:
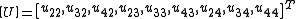
with
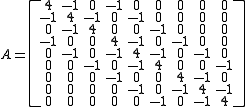
and
As can be seen, the boundary
's are brought to the right-hand-sideof the equation. The entire system is 9 × 9 while
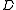and 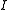are 3 × 3 and given by: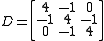and
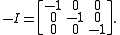
Methods of solution
Because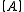 is block tridiagonal and sparse, many methods of solutionhave been developed to optimally solve this linear system for
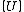.Among the methods are a generalized Thomas algorithm,
cyclic reduction, successive overrelaxation, and Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s. A theoretically optimal
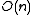solution can be computed using multigrid methods.Applications
In computational fluid dynamicsComputational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, for the solution of an incompressible flow problem, the incompressibility condition acts as a constraint for the pressure. There is no explicit form available for pressure in this case due to a strong coupling of the velocity and pressure fields. In this condition, by taking the divergence of all terms in the momentum equation, one obtains the pressure poisson equation. For an incompressible flow this constraint is given by:
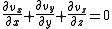
where
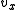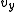is the velocity in the direction, isvelocity in
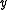and 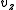is the velocity in the direction. Taking divergence of the momentum equation and using the incompressibility constraint, the pressure poisson equation is formed given by: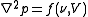where
is the kinematic viscosity of the fluid and 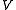is the velocity vector.The discrete Poisson's equation arises in the theory of
Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s. It appears as the relative value function for the dynamic programming equation in a Markov decision process
Markov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
, and as the control variate
Control variate
The control variates method is a variance reduction technique used in Monte Carlo methods. It exploits information about the errors in estimates of known quantities to reduce the error of an estimate of an unknown quantity.-Underlying principle:...
for application in simulation variance reduction.