
Discrete mathematics
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
structures
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
that are fundamentally discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
rather than continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. In contrast to real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, and statements in logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
– do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics therefore excludes topics in "continuous mathematics" such as calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. Discrete objects can often be enumerated
Enumeration
In mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...
by integers. More formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
s (sets that have the same cardinality as subsets of the natural numbers, including rational numbers but not real numbers). However, there is no exact, universally agreed, definition of the term "discrete mathematics." Indeed, discrete mathematics is described less by what is included than by what is excluded: continuously varying quantities and related notions.
The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometimes applied to parts of the field of discrete mathematics that deals with finite sets, particularly those areas relevant to business.
Research in discrete mathematics increased in the latter half of the twentieth century partly due to the development of digital computers which operate in discrete steps and store data in discrete bits. Concepts and notations from discrete mathematics are useful in studying and describing objects and problems in branches of computer science, such as computer algorithms, programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s, cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
, and software development
Software development
Software development is the development of a software product...
. Conversely, computer implementations are significant in applying ideas from discrete mathematics to real-world problems, such as in operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
.
Although the main objects of study in discrete mathematics are discrete objects, analytic methods from continuous mathematics are often employed as well.
Grand challenges, past and present

Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
, first stated in 1852, but not proved until 1976 (by Kenneth Appel and Wolfgang Haken, using substantial computer assistance).
In logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the second problem
Hilbert's second problem
In mathematics, Hilbert's second problem was posed by David Hilbert in 1900 as one of his 23 problems. It asks for a proof that arithmetic is consistent – free of any internal contradictions....
on David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's list of open problems
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
presented in 1900 was to prove that the axioms of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
are consistent. Gödel's second incompleteness theorem, proved in 1931, showed that this was not possible – at least not within arithmetic itself. Hilbert's tenth problem
Hilbert's tenth problem
Hilbert's tenth problem is the tenth on the list of Hilbert's problems of 1900. Its statement is as follows:Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite...
was to determine whether a given polynomial Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
with integer coefficients has an integer solution. In 1970, Yuri Matiyasevich
Yuri Matiyasevich
Yuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
proved that this could not be done.
The need to break
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
German codes in World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
led to advances in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, with the first programmable digital electronic computer
Colossus computer
Not to be confused with the fictional computer of the same name in the movie Colossus: The Forbin Project.Colossus was the world's first electronic, digital, programmable computer. Colossus and its successors were used by British codebreakers to help read encrypted German messages during World War II...
being developed at England's Bletchley Park
Bletchley Park
Bletchley Park is an estate located in the town of Bletchley, in Buckinghamshire, England, which currently houses the National Museum of Computing...
. At the same time, military requirements motivated advances in operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
. The Cold War
Cold War
The Cold War was the continuing state from roughly 1946 to 1991 of political conflict, military tension, proxy wars, and economic competition between the Communist World—primarily the Soviet Union and its satellite states and allies—and the powers of the Western world, primarily the United States...
meant that cryptography remained important, with fundamental advances such as public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
being developed in the following decades. Operations research remained important as a tool in business and project management, with the critical path method
Critical path method
The critical path method is an algorithm for scheduling a set of project activities. It is an important tool for effective project management.-History:...
being developed in the 1950s. The telecommunication
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
industry has also motivated advances in discrete mathematics, particularly in graph theory and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. Formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of statements in logic has been necessary for software development
Software development
Software development is the development of a software product...
of safety-critical systems, and advances in automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
have been driven by this need.
Computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
has been an important part of the computer graphics
Computer graphics (computer science)
Computer graphics is a sub-field of computer science which studies methods for digitally synthesizing and manipulating visual content. Although the term often refers to the study of three-dimensional computer graphics, it also encompasses two-dimensional graphics and image processing.- Overview...
incorporated into modern video games and computer-aided design
Computer-aided design
Computer-aided design , also known as computer-aided design and drafting , is the use of computer technology for the process of design and design-documentation. Computer Aided Drafting describes the process of drafting with a computer...
tools.
Several fields of discrete mathematics, particularly theoretical computer science, graph theory, and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, are important in addressing the challenging bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
problems associated with understanding the tree of life
Phylogenetic tree
A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the inferred evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical and/or genetic characteristics...
.
Currently, one of the most famous open problems in theoretical computer science is the P = NP problem, which involves the relationship between the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
and NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
. The Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
has offered a $1 million US prize for the first correct proof, along with prizes for six other mathematical problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
.
Theoretical computer science

Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
and logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
. Included within theoretical computer science is the study of algorithms for computing mathematical results. Computability studies what can be computed in principle, and has close ties to logic, while complexity studies the time taken by computations. Automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
and formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory are closely related to computability. Petri net
Petri net
A Petri net is one of several mathematical modeling languages for the description of distributed systems. A Petri net is a directed bipartite graph, in which the nodes represent transitions and places...
s and process algebras are used to model computer systems, and methods from discrete mathematics are used in analyzing VLSI electronic circuits. Computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
applies algorithms to geometrical problems, while computer image analysis applies them to representations of images. Theoretical computer science also includes the study of various continuous computational topics.
Information theory

Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
. Closely related is coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
which is used to design efficient and reliable data transmission and storage methods. Information theory also includes continuous topics such as: analog signal
Analog signal
An analog or analogue signal is any continuous signal for which the time varying feature of the signal is a representation of some other time varying quantity, i.e., analogous to another time varying signal. It differs from a digital signal in terms of small fluctuations in the signal which are...
s, analog coding, analog encryption.
Logic
Logic is the study of the principles of valid reasoning and inferenceInference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
, as well as of consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
, soundness
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
, and completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
. For example, in most systems of logic (but not in intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
) Peirce's law
Peirce's law
In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
(((P→Q)→P)→P) is a theorem. For classical logic, it can be easily verified with a truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
. The study of mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
is particularly important in logic, and has applications to automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
and formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of software.
Logical formulas
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
are discrete structures, as are proofs
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, which form finite trees
Tree structure
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
or, more generally, directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
structures (with each inference step
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
combining one or more premise
Premise
Premise can refer to:* Premise, a claim that is a reason for, or an objection against, some other claim as part of an argument...
branches to give a single conclusion). The truth values of logical formulas usually form a finite set, generally restricted to two values: true and false, but logic can also be continuous-valued, e.g., fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
. Concepts such as infinite proof trees or infinite derivation trees have also been studied, e.g. infinitary logic
Infinitary logic
An infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects, such as {blue, white, red} or the (infinite) set of all prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. Partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s and sets with other relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
have applications in several areas.
In discrete mathematics, countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
s (including finite sets) are the main focus. The beginning of set theory as a branch of mathematics is usually marked by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's work distinguishing between different kinds of infinite set, motivated by the study of trigonometric series, and further development of the theory of infinite sets is outside the scope of discrete mathematics. Indeed, contemporary work in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
makes extensive use of traditional continuous mathematics.
Combinatorics
Combinatorics studies the way in which discrete structures can be combined or arranged.Enumerative combinatorics
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
concentrates on counting the number of certain combinatorial objects - e.g. the twelvefold way
Twelvefold way
In combinatorics, the twelvefold way is a name given to a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number...
provides a unified framework for counting permutations, combinations and partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
.
Analytic combinatorics
Analytic combinatorics
Analytic combinatorics is a branch of combinatorics that describes combinatorial classes using generating functions, with formal power series that often correspond to analytic functions....
concerns the enumeration (i.e., determining the number) of combinatorial structures using tools from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. In contrast with enumerative combinatorics which uses explicit combinatorial formulae and generating functions to describe the results, analytic combinatorics aims at obtaining asymptotic formulae
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
.
Design theory is a study of combinatorial design
Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
s, which are collections of subsets with certain intersection properties.
Partition theory studies various enumeration and asymptotic problems related to integer partitions, and is closely related to q-series, special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
and orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
. Originally a part of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, partition theory is now considered a part of combinatorics or an independent field.
Order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
is the study of partially ordered sets, both finite and infinite.
Graph theory
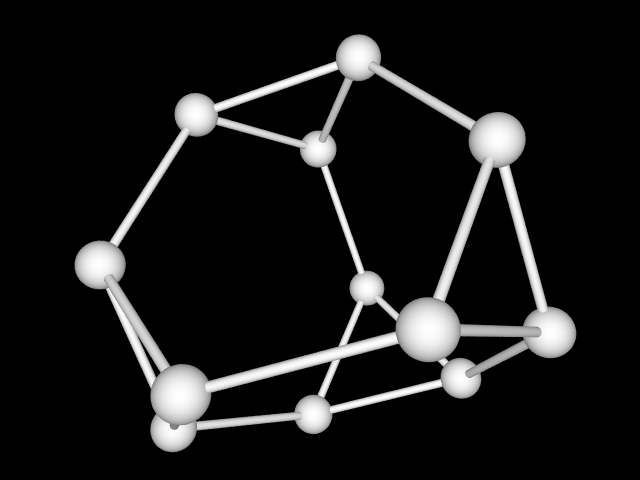
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
and network
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
s, is often considered part of combinatorics, but has grown large enough and distinct enough, with its own kind of problems, to be regarded as a subject in its own right. Graphs are one of the prime objects of study in Discrete Mathematics. They are among the most ubiquitous models of both natural and human-made
structures. They can model many types of relations and process dynamics in physical, biological and social systems. In computer science, they represent networks of communication, data organization, computational devices, the flow of computation, etc. In Mathematics, they are useful in Geometry and certain parts of Topology, e.g. Knot Theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. Algebraic graph theory
Algebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
has close links with group theory. There are also continuous graphs, however for the most part research in graph theory falls within the domain of discrete mathematics.
Probability
Discrete probability theory deals with events that occur in countable sample spaces. For example, count observations such as the numbers of birds in flocks comprise only natural number values {0, 1, 2, ...}. On the other hand, continuous observations such as the weights of birds comprise real number values and would typically be modeled by a continuous probability distribution such as the normal. Discrete probability distributions can be used to approximate continuous ones and vice versa. For highly constrained situations such as throwing diceDice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
or experiments with decks of cards, calculating the probability of events is basically enumerative combinatorics
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
.
Number theory

Number theory is concerned with the properties of numbers in general, particularly integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. It has applications to cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, cryptanalysis
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
, and cryptology, particularly with regard to modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, diophantine equations, linear and quadratic congruences, prime numbers and primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
ing. Other discrete aspects of number theory include geometry of numbers
Geometry of numbers
In number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
. In analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, techniques from continuous mathematics are also used. Topics that go beyond discrete objects include transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s, diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
and function fields
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
.
Algebra
Algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s occur as both discrete examples and continuous examples. Discrete algebras include: boolean algebra used in logic gate
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
s and programming; relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
used in databases; discrete and finite versions of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s are important in algebraic coding theory; discrete semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s and monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s appear in the theory of formal languages.
Calculus of finite differences, discrete calculus or discrete analysis
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on an interval of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is usually called a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. A sequence could be a finite sequence from some data source or an infinite sequence from a discrete dynamical system. Such a discrete function could be defined explicitly by a list (if its domain is finite), or by a formula for its general term, or it could be given implicitly by a recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
or difference equation. Difference equations are similar to a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, but replace differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
by taking the difference between adjacent terms; they can be used to approximate differential equations or (more often) studied in their own right. Many questions and methods concerning differential equations have counterparts for difference equations. For instance where there are integral transforms in harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
for studying continuous functions or analog signals, there are discrete transform
Discrete transform
In signal processing, discrete transforms are mathematical transforms, often linear transforms, of signals between discrete domains, such as between discrete time and discrete frequency....
s for discrete functions or digital signals. As well as the discrete metric there are more general discrete or finite metric spaces and finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
s.
Geometry

Discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
and combinatorial geometry are about combinatorial properties of discrete collections of geometrical objects. A long-standing topic in discrete geometry is tiling of the plane. Computational geometry applies algorithms to geometrical problems.
Topology
Although topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
is the field of mathematics that formalizes and generalizes the intuitive notion of "continuous deformation" of objects, it gives rise to many discrete topics; this can be attributed in part to the focus on topological invariants, which themselves usually take discrete values.
See combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
, topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
, topological combinatorics
Topological combinatorics
The discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....
, computational topology, discrete topological space, finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
, topology (chemistry)
Topology (chemistry)
In chemistry, topology provides a convenient way of describing and predicting the molecular structure within the constraints of three-dimensional space. Given the determinants of chemical bonding and the chemical properties of the atoms, topology provides a model for explaining how the atoms...
.
Operations research

Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
and other areas of optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, queuing theory, scheduling theory, network theory
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
. Operations research also includes continuous topics such as continuous-time Markov process, continuous-time martingales
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
, process optimization
Process optimization
Process optimization is the discipline of adjusting a process so as to optimize some specified set of parameters without violating some constraint. The most common goals are minimizing cost, maximizing throughput, and/or efficiency...
, and continuous and hybrid control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
.
Game theory, decision theory, utility theory, social choice theory
Decision theoryDecision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision.
Utility theory is about measures of the relative economic satisfaction from, or desirability of, consumption of various goods and services.
Social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
is about voting
Voting
Voting is a method for a group such as a meeting or an electorate to make a decision or express an opinion—often following discussions, debates, or election campaigns. It is often found in democracies and republics.- Reasons for voting :...
. A more puzzle-based approach to voting is ballot theory.
Game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
deals with situations where success depends on the choices of others, which makes choosing the best course of action more complex. There are even continuous games, see differential game
Differential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
. Topics include auction theory
Auction theory
Auction theory is an applied branch of economics which deals with how people act in auction markets and researches the properties of auction markets. There are many possible designs for an auction and typical issues studied by auction theorists include the efficiency of a given auction design,...
and fair division
Fair division
Fair division, also known as the cake-cutting problem, is the problem of dividing a resource in such a way that all recipients believe that they have received a fair amount...
.
Discretization
Discretization concerns the process of transferring continuous models and equations into discrete counterparts, often for the purposes of making calculations easier by using approximations. Numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
provides an important example.
Discrete analogues of continuous mathematics
There are many concepts in continuous mathematics which have discrete versions, such as discrete calculus, discrete probability distributions, discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
s, discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s, discrete differential geometry
Discrete differential geometry
Discrete differential geometry is the study of discrete counterparts of notions in differential geometry. Instead of smooth curves and surfaces, there are polygons, meshes, and simplicial complexes...
, discrete exterior calculus
Discrete exterior calculus
In mathematics, the discrete exterior calculus is the extension of the exterior calculus to discrete spaces including graphs and finite element meshes. DEC methods have proved to be very powerful in improving and analyzing finite element methods: for instance, DEC-based methods allow the use of...
, discrete Morse theory, difference equations, discrete dynamical systems, and discrete vector measures.
In applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, discrete modelling
Discrete modelling
Discrete modelling is the discrete analogue of continuous modelling. In discrete modelling, discrete formulae are fit to data. A common method in this form of modelling is to use recurrence relations....
is the discrete analogue of continuous modelling
Continuous modelling
Continuous modelling is the mathematical practice of applying a model to continuous data...
. In discrete modelling, discrete formulae are fit to data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. A common method in this form of modelling is to use recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s.
Hybrid discrete and continuous mathematics
The time scale calculusTime scale calculus
In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
is a unification of the theory of difference equations with that of differential equations, which has applications to fields requiring simultaneous modelling of discrete and continuous
See also
- Outline of discrete mathematics
- CyberChaseCyberchaseCyberchase is an American educational television series for children age 6-12, that teaches children discrete mathematics. The show airs on Public Broadcasting Service and PBS Kids GO! in the United States. Seasons one through five were produced by Thirteen/WNET New York and Nelvana...
, a show that teaches Discrete Mathematics to children
Further reading
- Norman L. BiggsNorman L. BiggsNorman Linstead Biggs is a mathematician focusing on discrete mathematics and in particular algebraic combinatorics, and his interests include computational learning theory, history of mathematics and historical metrology. As of 2006 he is Emeritus Professor at The London School of...
, Discrete Mathematics 2nd ed. Oxford University Press. ISBN 0-19-850717-8, and companion web site including questions together with solutions. - Ronald GrahamRonald GrahamRonald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
, Donald E. KnuthDonald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
, Oren PatashnikOren PatashnikOren Patashnik is a computer scientist. He is notable for co-creating BibTeX, and co-writing Concrete Mathematics: A Foundation for Computer Science...
, Concrete MathematicsConcrete MathematicsConcrete Mathematics: A Foundation for Computer Science, by Ronald Graham, Donald Knuth, and Oren Patashnik, is a mathematical textbook that is widely used in computer-science departments. It provides mathematical knowledge and skills for computer science, especially for the analysis of algorithms... - Donald E. Knuth, The Art of Computer ProgrammingThe Art of Computer ProgrammingThe Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
ISBN 978-0321751041. - Kenneth H. RosenKenneth H. RosenKenneth H. Rosen is a notable author and mathematician. His interests include discrete mathematics and number theory. He is the successful author of several books including Discrete Mathematics and Its Applications, McGraw-Hill. He holds degrees in mathematics from the University of Michigan Ann...
, Handbook of Discrete and Combinatorial Mathematics CRC Press. ISBN 0-8493-0149-1. - Richard JohnsonbaughRichard JohnsonbaughRichard Johnsonbaugh is a notable author and mathematician. His interests include discrete mathematics and the history of mathematics. He is the successful author of several books including Discrete Mathematics, 7th ed, Macmillan. He holds degrees in computer science and mathematics from the...
, Discrete Mathematics 6th ed. Macmillan. ISBN 0-13-045803-1, and companion web site. - John DwyerJohn DwyerJohn Dwyer may refer to:*John Dwyer *John Dwyer , 19th-century baseball player*John Dwyer , American*John Dwyer , Australian*John M. Dwyer, set decorator*John Dwyer...
& Suzy Jagger, Discrete Mathematics for Business & Computing, 1st ed. 2010 ISBN 978-1907934001. - Kenneth H. RosenKenneth H. RosenKenneth H. Rosen is a notable author and mathematician. His interests include discrete mathematics and number theory. He is the successful author of several books including Discrete Mathematics and Its Applications, McGraw-Hill. He holds degrees in mathematics from the University of Michigan Ann...
, Discrete Mathematics and Its Applications 6th ed. McGraw Hill. ISBN 0-07-288008-2, and companion web site. - Ralph P. GrimaldiRalph GrimaldiRalph Peter Grimaldi is an American mathematician specializing in discrete mathematics who is a full professor at Rose-Hulman Institute of Technology...
, Discrete and Combinatorial Mathematics: An Applied Introduction 5th ed. Addison Wesley. ISBN 0-20-172634-3 - Susanna S. EppSusanna S. EppSusanna S. Epp is a notable author and mathematician. Her interests include discrete mathematics and mathematical logic. She is the successful author of several books including Discrete Mathematics with Applications, Thomson Brooks/Cole. She holds degrees in mathematics from the University of...
, Discrete Mathematics with Applications Brooks Cole. ISBN 978-0495391326 - Jiří MatoušekJirí Matoušek (mathematician)Jiří Matoušek is a Czech mathematician working in computational geometry. He is a professor at Charles University in Prague and is the author of several textbooks and research monographs....
& Jaroslav NešetřilJaroslav NešetrilJaroslav Nešetřil is a Czech mathematician, working at Charles University in Prague. His research areas include combinatorics , graph theory , algebra , posets , computer science .Nešetřil...
, Invitation to Discrete Mathematics, OUP, ISBN 978-0198502081. - Mathematics Archives, Discrete Mathematics links to syllabi, tutorials, programs, etc.
- Andrew SimpsonAndrew Clive SimpsonDr Andrew Clive Simpson is a British Computer Scientist. He is Director of Studies, Software Engineering Programme at University of Oxford. He is Governing Body Fellow of Kellogg College.-Biography:...
, Discrete Mathematics by Example McGraw Hill. ISBN 0-07-709840-4

