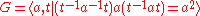Dehn function
Encyclopedia
In the mathematical subject of geometric group theory
, a Dehn function, named after Max Dehn
, is an optimal function associated to a finite group presentation which bounds the area of a relation in that group (that is a freely reduced word in the generators representing the identity element
of the group) in terms of the length of that relation (see pp. 79–80 in ). The growth type of the Dehn function is a quasi-isometry invariant
of a finitely presented group. The Dehn function of a finitely presented group is also closely connected with non-deterministic algorithmic complexity of the word problem
in groups. In particular, a finitely presented group has solvable word problem
if and only if the Dehn function for a finite presentation of this group is recursive
(see Theorem 2.1 in ). The notion of a Dehn function is motivated by isoperimetric problems in geometry, such as the classic isoperimetric inequality for the Euclidean plane and, more generally, the notion of a filling area function that estimates the area of a minimal surface
in a Riemannian manifold
in terms of the length of the boundary curve of that surface.
in 1910s. Dehn proved that the word problem
for the standard presentation of the fundamental group
of a closed oriented surface of genus at least two is solvable by what is now called Dehn's algorithm
. A direct consequence of this fact is that for this presentation the Dehn function satisfies Dehn(n) ≤ n. This result was extended in 1960s by Martin Greendlinger to finitely presented groups satisfying the C'(1/6) small cancellation condition
. The formal notion of an isoperimetric function and a Dehn function as it is used today appeared in late 1980s – early 1990s together with the introduction and development of the theory of word-hyperbolic groups. In his 1987 monograph "Hyperbolic groups" Gromov proved that a finitely presented group is word-hyperbolic if and only if it satisfies a linear isoperimetric inequality, that is, if and only if the Dehn function of this group is equivalent to the function f(n) = n. Gromov's proof was in large part informed by analogy with filling area functions for compact Riemannian manifold
s where the area of a minimal surface
bounding a null-homotopic closed curve is bounded in terms of the length of that curve.
The study of isoperimetric and Dehn functions quickly developed into a separate major theme in geometric group theory
, especially since the growth types of these functions are natural quasi-isometry
invariants of finitely presented groups. One of the major results in the subject was obtained by Sapir, Birget and Rips
who showed that most "reasonable" time complexity functions of Turing machine
s can be realized, up to natural equivalence, as Dehn functions of finitely presented groups.
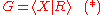
be a finite group presentation where the X is a finite alphabet and where R ⊆ F(X) is a finite set of cyclically reduced words.
of R in F(X), that is, there exists a representation of w as
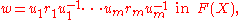 (♠)
(♠)
where m ≥ 0 and where ri ∈ R± 1 for i = 1, ..., m.
For w ∈ F(X) satisfying w = 1 in G, the area of w with respect to (∗), denoted Area(w), is the smallest m ≥ 0 such that there exists a representation (♠) for w as the product in F(X) of m conjugates of elements of R± 1.
A freely reduced word w ∈ F(X) satisfies w = 1 in G if and only if the loop labeled by w in the presentation complex
for G corresponding to (∗) is null-homotopic. This fact can be used to show that Area(w) is the smallest number of 2-cells in a van Kampen diagram
over (∗) with boundary cycle labelled by w.

such that whenever w ∈ F(X) is a freely reduced word satisfying w = 1 in G, then
where |w| is the length of the word w.

Equivalently, Dehn(n) is the smallest isoperimetric function for (∗), that is, Dehn(n) is an isoperimetric function for (∗) and for any other isoperimetric function f(n) we have
for every n ≥ 0.
For two monotone-nondecreasing functions
one says that f is dominated by g if there exists C ≥1 such that
for every integer n ≥ 0. Say that f ≈ g if f is dominated by g and g is dominated by f. Then ≈ is an equivalence relation
and Dehn functions and isoperimetric functions are usually studied up to this equivalence relation.
Thus for any a,b > 1 we have an ≈ bn. Similarly, if f(n) is a polynomial of degree d (where d ≥ 1 is a real number) with non-negative coefficients, then f(n) ≈ nd. Also, 1 ≈ n.
If a finite group presentation admits an isopeprimetric function f(n) that is equivalent to a linear (respectively, quadratic, cubic, polynomial, exponential, etc.) function in n, the presentation is said to satisfy a linear (respectively, quadratic, cubic, polynomial, exponential, etc.) isoperimetric inequality.
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, a Dehn function, named after Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
, is an optimal function associated to a finite group presentation which bounds the area of a relation in that group (that is a freely reduced word in the generators representing the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of the group) in terms of the length of that relation (see pp. 79–80 in ). The growth type of the Dehn function is a quasi-isometry invariant
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
of a finitely presented group. The Dehn function of a finitely presented group is also closely connected with non-deterministic algorithmic complexity of the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
in groups. In particular, a finitely presented group has solvable word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
if and only if the Dehn function for a finite presentation of this group is recursive
Recursive function
Recursive function may refer to:*Recursion , a procedure or subroutine, implemented in a programming language, whose implementation references itself*A total computable function, a function which is defined for all possible inputs...
(see Theorem 2.1 in ). The notion of a Dehn function is motivated by isoperimetric problems in geometry, such as the classic isoperimetric inequality for the Euclidean plane and, more generally, the notion of a filling area function that estimates the area of a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
in a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in terms of the length of the boundary curve of that surface.
History
The idea of an isoperimetric function for a finitely presented group goes back to the work of Max DehnMax Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
in 1910s. Dehn proved that the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
for the standard presentation of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a closed oriented surface of genus at least two is solvable by what is now called Dehn's algorithm
Small cancellation theory
In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial...
. A direct consequence of this fact is that for this presentation the Dehn function satisfies Dehn(n) ≤ n. This result was extended in 1960s by Martin Greendlinger to finitely presented groups satisfying the C'(1/6) small cancellation condition
Small cancellation theory
In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial...
. The formal notion of an isoperimetric function and a Dehn function as it is used today appeared in late 1980s – early 1990s together with the introduction and development of the theory of word-hyperbolic groups. In his 1987 monograph "Hyperbolic groups" Gromov proved that a finitely presented group is word-hyperbolic if and only if it satisfies a linear isoperimetric inequality, that is, if and only if the Dehn function of this group is equivalent to the function f(n) = n. Gromov's proof was in large part informed by analogy with filling area functions for compact Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s where the area of a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
bounding a null-homotopic closed curve is bounded in terms of the length of that curve.
The study of isoperimetric and Dehn functions quickly developed into a separate major theme in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, especially since the growth types of these functions are natural quasi-isometry
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
invariants of finitely presented groups. One of the major results in the subject was obtained by Sapir, Birget and Rips
Eliyahu Rips
Eliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
who showed that most "reasonable" time complexity functions of Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s can be realized, up to natural equivalence, as Dehn functions of finitely presented groups.
Formal definition
Let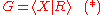
be a finite group presentation where the X is a finite alphabet and where R ⊆ F(X) is a finite set of cyclically reduced words.
Area of a relation
Let w ∈ F(X) be a relation in G, that is, a freely reduced word such that w = 1 in G. Note that this is equivalent to saying that is, w belongs to the normal closureNormal closure
The term normal closure is used in two senses in mathematics:* In group theory, the normal closure of a subset of a group is the smallest normal subgroup that contains the subset; see conjugate closure....
of R in F(X), that is, there exists a representation of w as
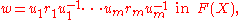 (♠)
(♠)where m ≥ 0 and where ri ∈ R± 1 for i = 1, ..., m.
For w ∈ F(X) satisfying w = 1 in G, the area of w with respect to (∗), denoted Area(w), is the smallest m ≥ 0 such that there exists a representation (♠) for w as the product in F(X) of m conjugates of elements of R± 1.
A freely reduced word w ∈ F(X) satisfies w = 1 in G if and only if the loop labeled by w in the presentation complex
Presentation complex
In geometric group theory, a presentation complex is a 2-dimensional cell complex associated to any presentation of a group G. The complex has a single vertex, and one loop at the vertex for each generator of G...
for G corresponding to (∗) is null-homotopic. This fact can be used to show that Area(w) is the smallest number of 2-cells in a van Kampen diagram
Van Kampen diagram
In the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
over (∗) with boundary cycle labelled by w.
Isoperimetric function
An isoperimetric function for a finite presentation (∗) is a monotone non-decreasing function
such that whenever w ∈ F(X) is a freely reduced word satisfying w = 1 in G, then
- Area(w) ≤ f(|w|),
where |w| is the length of the word w.
Dehn function
Then the Dehn function of a finite presentation (∗) is defined as
Equivalently, Dehn(n) is the smallest isoperimetric function for (∗), that is, Dehn(n) is an isoperimetric function for (∗) and for any other isoperimetric function f(n) we have
- Dehn(n) ≤ f(n)
for every n ≥ 0.
Growth types of functions
Because Dehn functions are usually difficult to compute precisely, one usually studies their asymptotic growth types as n tends to infinity.For two monotone-nondecreasing functions

one says that f is dominated by g if there exists C ≥1 such that

for every integer n ≥ 0. Say that f ≈ g if f is dominated by g and g is dominated by f. Then ≈ is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and Dehn functions and isoperimetric functions are usually studied up to this equivalence relation.
Thus for any a,b > 1 we have an ≈ bn. Similarly, if f(n) is a polynomial of degree d (where d ≥ 1 is a real number) with non-negative coefficients, then f(n) ≈ nd. Also, 1 ≈ n.
If a finite group presentation admits an isopeprimetric function f(n) that is equivalent to a linear (respectively, quadratic, cubic, polynomial, exponential, etc.) function in n, the presentation is said to satisfy a linear (respectively, quadratic, cubic, polynomial, exponential, etc.) isoperimetric inequality.
Basic properties
- If G and H are quasi-isometricQuasi-isometryIn mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
finitely presented groups and some finite presentation of G has an isoperimetric function f(n) then for any finite presentation of H there is an isoperimentric function equivalent to f(n). In particular, this fact holds for G = H, where the same group is given by two different finite presentations. - Consequently, for a finitely presented group the growth type of its Dehn function, in the sense of the above definition, does not depend on the choice of a finite presentation for that group. More generally, if two finitely presented groups are quasi-isometricQuasi-isometryIn mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
then their Dehn functions are equivalent. - For a finitely presented group G given by a finite presentation (∗) the following conditions are equivalent:
- G has a recursiveRecursive functionRecursive function may refer to:*Recursion , a procedure or subroutine, implemented in a programming language, whose implementation references itself*A total computable function, a function which is defined for all possible inputs...
Dehn function with respect to (∗) - There exists a recursive isoperimetric function f(n) for (∗).
- The group G has solvable word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
.
- G has a recursive
-
- In particular, this implies that solvability of the word problem is a quasi-isometry invariant for finitely presented groups.
- Knowing the area Area(w) of a relation w allows to bound, in terms of |w|, not only the number of conjugates of the defining relations in (♠) but the lengths of the conjugating elements ui as well. As a consequence, it is known that if a finitely presented group G given by a finite presentation (∗) has computable Dehn function Dehn(n), then the word problem for G is solvable with non-deterministic time complexity Dehn(n) and deterministic time complexityDeterministic algorithmIn computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
Exp(Dehn(n)). However, in general there is no reasonable bound on the Dehn function of a finitely presented group in terms of the deterministic time complexity of the word problem and the gap between the two functions can be quite large.
- Knowing the area Area(w) of a relation w allows to bound, in terms of |w|, not only the number of conjugates of the defining relations in (♠) but the lengths of the conjugating elements ui as well. As a consequence, it is known that if a finitely presented group G given by a finite presentation (∗) has computable Dehn function Dehn(n), then the word problem for G is solvable with non-deterministic time complexity Dehn(n) and deterministic time complexity
- In particular, this implies that solvability of the word problem is a quasi-isometry invariant for finitely presented groups.
Examples
- For any finite presentation of a finite group G we have Dehn(n) ≈ n.
- For the closed oriented surface of genus 2, the standard presentation of its fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
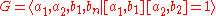
- satisfies Dehn(n) ≤ n and Dehn(n) ≈ n.
- For every integer k ≥ 2 the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
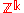 has Dehn(n) ≈ n2.
has Dehn(n) ≈ n2. - The Baumslag-Solitar group
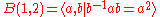
- For every integer k ≥ 2 the free abelian group
- has Dehn(n) ≈ 2n (see ).
- The 3-dimensional discrete Heisenberg group
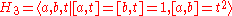
- The 3-dimensional discrete Heisenberg group
- satisfies a cubic but no quadratic isoperimetric inequality.
- Higher-dimensional Heisenberg groups
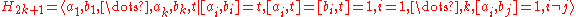 ,
,
- Higher-dimensional Heisenberg groups
- where k ≥ 2, satisfy quadratic isoperimetric inequalities.
- If G is a "Novikov-Boone group", that is, a finitely presented group with unsolvable word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
, then the Dehn function of G growths faster than any recursive functionRecursive functionRecursive function may refer to:*Recursion , a procedure or subroutine, implemented in a programming language, whose implementation references itself*A total computable function, a function which is defined for all possible inputs...
. - For the Thompson groupThompson groupsIn mathematics, the Thompson groups are three groups, commonly denoted F, T and V, which were first studied by the logician Richard Thompson in 1965...
F the Dehn function is quadratic, that is, equivalent to n2 (see ). - The so-called Baumslag-Gersten group
- If G is a "Novikov-Boone group", that is, a finitely presented group with unsolvable word problem
- has a Dehn function growing faster than any fixed iterated tower of exponentials. Specifically, for this group
- Dehn(n) ≈ exp(exp(exp(...(exp(1))...)))
- where the number of exponentials is equal to the integral part of log2(n) (see ).
Known results
- A finitely presented group is word-hyperbolic group if and only if its Dehn function is equivalent to n, that is, if and only if every finite presentation of this group satisfies a linear isoperimetric inequality.
- Isoperimetric gap: If a finitely presented group satisfies a subquadratic isoperimetric inequality then it is word-hyperbolic. Thus there are no finitely presented groups with Dehn functions equivalent to nd with d ∈ (1,2).
- Automatic groupAutomatic groupIn mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
s and, more generally, combable groups satisfy quadratic isoperimetric inequalities. - A finitely generated nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
has a Dehn function equivalent to nd where d ≥ 1 and all positive integers d are realized in this way. Moreover, every finitely generated nilpotent group G admits a polynomial isoperimetric inequality of degree c + 1, where c is the nilpotency class of G. - The set of real numbers d ≥ 1, such that there exists a finitely presented group with Dehn function equivalent to nd, is dense in the interval
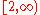 .
. - If all asymptotic conesUltralimitIn mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter to avoid the process of repeatedly passing...
of a finitely presented group are simply connectedSimply connected spaceIn topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
, then the group satisfies a polynomial isoperimetric inequality. - If a finitely presented group satisfies a quadratic isoperimetric inequality, then all asymptotic cones of this group are simply connected.
- If (M,g) is a closed Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and G = π1(M) then the Dehn function of G is equivalent to the filling area function of the manifold. - If G is a group acting properly discontinuously and cocompactly by isometries on a CAT(0) space, then G satisfies a quadratic isoperimetric inequality. In particular, this applies to the case where G is the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a closed Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of non-positive sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
(not necessarily constant). - The Dehn function of SL(m, Z) is at most exponential for any m ≥ 3. For SL(3,Z) this bound is sharp and it is known in that case that the Dehn function does not admit a subexponential upper bound. The Dehn functions for SL(m,Z), where m > 4 are quadratic. The Dehn function of SL(4,Z), has been conjectured to be quadratic, by Thurston.
- Mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
s of surfaces of finite type are automaticAutomatic groupIn mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
and satisfy quadratic isoperimetric inequalities. - Hatcher and Vogtmann proved that the groups Aut(Fk) and Out(Fk) satisfy exponential isoperimetric inequalities for every k ≥ 3. For k = 3 these bounds are known to be sharp by a result of Bridson and Vogtamann who proved that Aut(F3) and Out(F3) do not satisfy subexponential isoperimetric inequalities.
- For every automorphism φ of a finitely generated free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
Fk the mapping torus group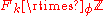 of φ satisfies a quadratic isoperimetric inequality.
of φ satisfies a quadratic isoperimetric inequality. - Most "reasonable" computable functions that are ≥n4, can be realized, up to equivalence, as Dehn functions of finitely presented groups. In particular, if f(n) ≥ n4 is a superadditive function whose binary representation is computable in time
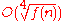 by a Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
by a Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
then f(n) is equivalent to the Dehn function of a finitely presented group. - Although one cannot reasonably bound the Dehn function of a group in terms of the complexity of its word problem, Birget, Olʹshanskii, RipsEliyahu RipsEliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
and Sapir obtained the following result, providing a far-reaching generalization of Higman's embedding theoremHigman's embedding theoremIn group theory, Higman's embedding theorem states that every finitely generated recursively presented group R can be embedded as a subgroup of some finitely presented group G...
: The word problem of a finitely generated group is decidable in nondeterministic polynomial time if and only if this group can be embedded into a finitely presented group with a polynomial isoperimetric function. Moreover, every group with the word problem solvable in time T(n) can be embedded into a group with isoperimetric function equivalent to n2T(n2)4.
Generalizations
- There are several companion notions closely related to the notion of an isoperimetric function. Thus an isodiametric function bounds the smallest diameter (with respect to the simplicial metric where every edge has length one) of a van Kampen diagramVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
for a particular relation w in terms of the length of w. A filling length function the smallest filling length of a van Kampen diagramVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
for a particular relation w in terms of the length of w. Here the filling length of a diagram is the mimimum, over all combinatorial null-homotopies of the diagram, of the maximal length of intermediate loops bounding intermediate diagrams along such null-homotopies. The filling length function is closely related to the non-deterministic space complexity of the word problem for finitely presented groups. There are several general inequalities connecting the Dehn function, the optimal isodiametric function and the optimal filling length function, but the precise relationship between them is not yet understood.
- There are also higher-dimensional generalizations of isoperimetric and Dehn functions. For k ≥ 1 the k-dimensional isoperimetric function of a group bounds the minimal combinatorial volume of (k + 1)-dimensional ball-fillings of k-spheres mapped into a k-connected space on which the group acts properly and cocompactly; the bound is given as a function of the combinatorial volume of the k-sphere. The standard notion of an isoperimetric function corresponds to the case k = 1. Unlike the case of standard Dehn functions, little is known about possible growth types of k-dimensional isoperimetric functions of finitely presented groups for k ≥ 2.
- In his monograph Asymptotic invariants of infinite groups Gromov proposed a probabilistic or averaged version of Dehn function and suggested that for many groups averaged Dehn functions should have strictly slower asymptotics than the standard Dehn functions. More precise treatments of the notion of an averaged Dehn function or mean Dehn function were given later by other researchers who also proved that indeed averaged Dehn functions are subasymptotic to standard Dehn functions in a number of cases (such as nilpotent and abelian groups).
- A relative version of the notion of an isoperimetric function plays a central role in Osin' approach to relatively hyperbolic groupRelatively hyperbolic groupIn mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
s.
- GrigorchukRostislav GrigorchukRostislav Ivanovich Grigorchuk is a Soviet and Ukrainian mathematician working in the area of group theory. He holds the rank of Distinguished Professor in the Mathematics Department of Texas A&M University...
and Ivanov explored several natural generalizations of Dehn function for group presentations on finitely many generators but with infinitely many defining relations.
See also
- van Kampen diagramVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
- Word-hyperbolic group
- Automatic groupAutomatic groupIn mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
- Small cancellation theorySmall cancellation theoryIn the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial...
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
Further reading
- Noel Brady, Tim Riley and Hamish Short. The Geometry of the Word Problem for Finitely Generated Groups. Advanced Courses in Mathematics CRM Barcelona, Birkhäuser, Basel, 2007. ISBN 3764379499.
- Martin R. Bridson. The geometry of the word problem. Invitations to geometry and topology, pp. 29–91, Oxford Graduate Texts in Mathematics, 7, Oxford University PressOxford University PressOxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
, Oxford, 2002. ISBN 0-19-850772-0.
External links
- The Isoperimetric Inequality for SL(n,Z). A September 2008 Workshop at the American Institute of MathematicsAmerican Institute of MathematicsThe American Institute of Mathematics was founded in 1994 by John Fry and is located in Palo Alto, California. Privately funded by Fry at inception, in 2002, AIM became one of eight NSF-funded mathematical institutes....
. - A collection of diagrams by Tim Riley