
Convex conjugate
Encyclopedia
In mathematics
, convex conjugation is a generalization of the Legendre transformation
. It is also known as Legendre–Fenchel transformation or Fenchel transformation (after Adrien-Marie Legendre
and Werner Fenchel
).
 be a real
be a real
normed vector space
, and let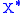 be the dual space
be the dual space
to . Denote the dual pair
. Denote the dual pair
ing by

For a functional
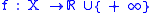
taking values on the extended real number line
the convex conjugate

is defined in terms of the supremum
by
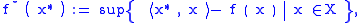
or, equivalently, in terms of the infimum
by
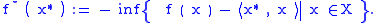
This definition can be interpreted as an encoding of the convex hull
of the function's epigraph
in terms of its supporting hyperplane
s. http://maze5.net/?page_id=733
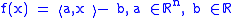
is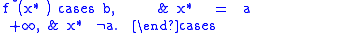
The convex conjugate of a power function
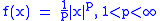
is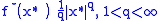
where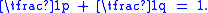
The convex conjugate of the absolute value
function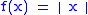
is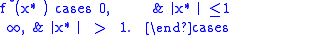
The convex conjugate of the exponential function
 is
is
Convex conjugate and Legendre transform of the exponential function agree except that the domain
of the convex conjugate is strictly larger as the Legendre transform is only defined for positive real numbers.
of a random variable
X. Then
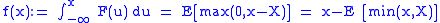
has the convex conjugate
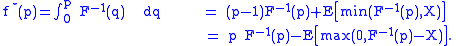
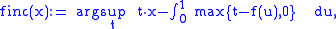
as this is a nondecreasing rearrangement of the initial function f; in particular,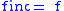 for ƒ nondecreasing.
for ƒ nondecreasing.
is again a closed convex function. The convex conjugate of a polyhedral convex function (a convex function with polyhedral
epigraph
) is again a polyhedral convex function.
Convex-conjugation is order-reversing
: if then
then 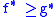 . Here
. Here
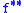 (the convex conjugate of the convex conjugate) is also the closed convex hull, i.e. the largest lower semi-continuous convex function with
(the convex conjugate of the convex conjugate) is also the closed convex hull, i.e. the largest lower semi-continuous convex function with 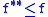 . For proper functions
. For proper functions
f, f = f** if and only if
f is convex and lower semi-continuous.
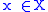 and
and 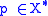 :
:
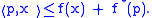
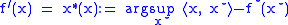 and
and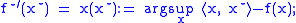
whence
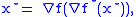
and moreover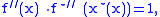
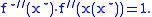
 ,
, 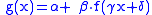 , then
, then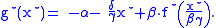
In case of an additional parameter (α, say) moreover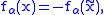
where is chosen to be the maximizing argument.
is chosen to be the maximizing argument.
from Rn to Rm. For any convex function f on Rn, one has
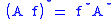
where A* is the adjoint operator of A defined by
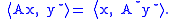
A closed convex function f is symmetric with respect to a given set G of orthogonal linear transformation
s,

if and only if its convex conjugate f* is symmetric with respect to G.
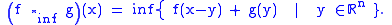
Let f1, …, fm be proper convex functions on Rn. Then
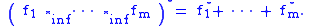
The infimal convolution of two functions has a geometric interpretation: The (strict) epigraph
of the infimal convolution of two functions is the Minkowski sum of the (strict) epigraphs of those functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, convex conjugation is a generalization of the Legendre transformation
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
. It is also known as Legendre–Fenchel transformation or Fenchel transformation (after Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
and Werner Fenchel
Werner Fenchel
Moritz Werner Fenchel was a mathematician known for his contributions to geometry and to optimization theory. Fenchel established the basic results of convex analysis and nonlinear optimization theory. Fenchel's monographs and lecture-notes were very influential also...
).
Definition
Let be a real
be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, and let
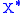 be the dual space
be the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
to
 . Denote the dual pair
. Denote the dual pairDual pair
In functional analysis and related areas of mathematics a dual pair or dual system is a pair of vector spaces with an associated bilinear form....
ing by

For a functional
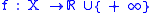
taking values on the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
the convex conjugate

is defined in terms of the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
by
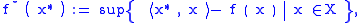
or, equivalently, in terms of the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
by
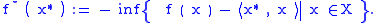
This definition can be interpreted as an encoding of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the function's epigraph
Epigraph (mathematics)
In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
in terms of its supporting hyperplane
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
s. http://maze5.net/?page_id=733
Examples
The convex conjugate of an affine function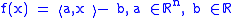
is
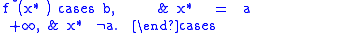
The convex conjugate of a power function
Power function
In mathematics, a power function is a function of the form , where c and a are constant real numbers and x is a variable.Power functions are a special case of power law relationships, which appear throughout mathematics and statistics....
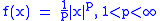
is
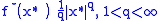
where
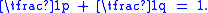
The convex conjugate of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function
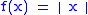
is
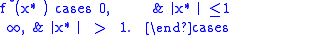
The convex conjugate of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
 is
is
Convex conjugate and Legendre transform of the exponential function agree except that the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the convex conjugate is strictly larger as the Legendre transform is only defined for positive real numbers.
Connection with average value at risk
Let F denote a cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X. Then
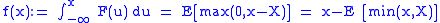
has the convex conjugate
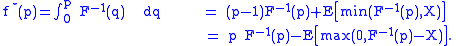
Ordering
A particular interpretation has the transform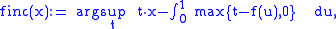
as this is a nondecreasing rearrangement of the initial function f; in particular,
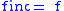 for ƒ nondecreasing.
for ƒ nondecreasing.Properties
The convex conjugate of a closed convex functionClosed convex function
In mathematics, a convex function is called closed if its epigraph is a closed set.- Properties :A closed convex function f is the pointwise supremum of the collection of all affine functions h such that h≤f.- References :...
is again a closed convex function. The convex conjugate of a polyhedral convex function (a convex function with polyhedral
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
epigraph
Epigraph (mathematics)
In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
) is again a polyhedral convex function.
Convex-conjugation is order-reversing
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
: if
 then
then 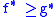 . Here
. HereBiconjugate
The convex conjugate of a function is always lower semi-continuous. The biconjugate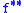 (the convex conjugate of the convex conjugate) is also the closed convex hull, i.e. the largest lower semi-continuous convex function with
(the convex conjugate of the convex conjugate) is also the closed convex hull, i.e. the largest lower semi-continuous convex function with 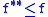 . For proper functions
. For proper functionsProper convex function
In mathematical analysis and optimization, a proper convex function is a convex function f taking values in the extended real number line such thatf -\infty...
f, f = f** if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
f is convex and lower semi-continuous.
Fenchel's inequality
For any function f and its convex conjugate f* Fenchel's inequality (also known as the Fenchel-Young inequality) holds for every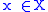 and
and 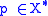 :
: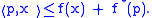
Maximizing argument
It is interesting to observe that the derivative of the function is the maximizing argument to compute the convex conjugate: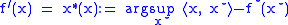 and
and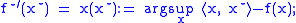
whence

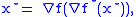
and moreover
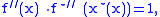
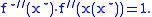
Scaling properties
If, for some ,
, 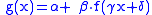 , then
, then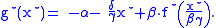
In case of an additional parameter (α, say) moreover
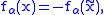
where
 is chosen to be the maximizing argument.
is chosen to be the maximizing argument.Behavior under linear transformations
Let A be a linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
from Rn to Rm. For any convex function f on Rn, one has
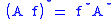
where A* is the adjoint operator of A defined by
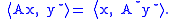
A closed convex function f is symmetric with respect to a given set G of orthogonal linear transformation
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
s,

if and only if its convex conjugate f* is symmetric with respect to G.
Infimal convolution
The infimal convolution of two functions f and g is defined as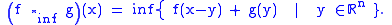
Let f1, …, fm be proper convex functions on Rn. Then
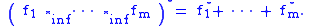
The infimal convolution of two functions has a geometric interpretation: The (strict) epigraph
Epigraph (mathematics)
In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
of the infimal convolution of two functions is the Minkowski sum of the (strict) epigraphs of those functions.
See also
- Dual problemDual problemIn constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
- Fenchel's duality theoremFenchel's duality theoremIn mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel.Let ƒ be a proper convex function on Rn and let g be a proper concave function on Rn...
- Legendre transformationLegendre transformationIn mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
- Young's inequalityYoung's inequalityIn mathematics, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution of two functions. They are named for William Henry Young....


