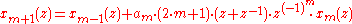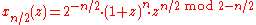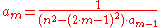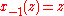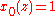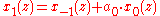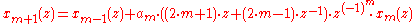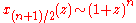Cohen-Daubechies-Feauveau wavelet
Encyclopedia
Biorthogonal wavelet
A biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets...
s, which was made popular by Ingrid Daubechies
Ingrid Daubechies
Ingrid Daubechies is a Belgian physicist and mathematician. She was between 2004 and 2011 the William R. Kenan Jr. Professor in the mathematics and applied mathematics departments at Princeton University. In January 2011 she moved to Duke University as a Professor in mathematics. She is the first...
. These are not the same as the orthogonal Daubechies wavelet
Daubechies wavelet
Named after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
s, and also not very similar in shape and properties. However their construction idea is the same.
The JPEG 2000
JPEG 2000
JPEG 2000 is an image compression standard and coding system. It was created by the Joint Photographic Experts Group committee in 2000 with the intention of superseding their original discrete cosine transform-based JPEG standard with a newly designed, wavelet-based method...
compression
Image compression
The objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
standard uses the biorthogonal CDF 5/3 wavelet (also called the LeGall 5/3 wavelet) for lossless compression and a CDF 9/7 wavelet for lossy compression.
Properties
- The primal generator is a B-splineB-splineIn the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
if the simple factorization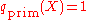
(see below) is chosen - The dual generator has the maximum number of smoothness factors which is possible for its length.
- All generators and wavelets in this family are symmetric.
Construction
For every positive integer A there exists a unique polynomial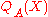
of degree A-1 satisfying the identity
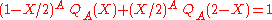.This is the same polynomial as used in the construction of the
Daubechies wavelet
Daubechies wavelet
Named after Ingrid Daubechies, the Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support...
s. But, instead of a spectral factorization,
here we try to factor
,where the factors are polynomials with real coefficients and
constant coefficient 1. Then,
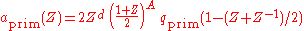
and
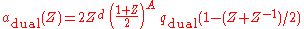
form a biorthogonal pair of scaling sequences. d is some integer used to
center the symmetric sequences at zero or to make the corresponding discrete filters
causal.
Depending on the roots of
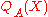, there may be up to
different factorizations. A simple factorization is
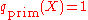and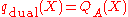 
, thenthe
scaling function is the B-splineB-spline
In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
of order
A-1. For A=1 one obtains the orthogonal Haar wavelet
Haar wavelet
In mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
.
Tables of coefficients
For A=2 one obtains in this way the LeGall 5/3-wavelet:| A | QA(X) | qprim(X) | qdual(X) | aprim(Z) | adual(Z) |
|---|---|---|---|---|---|
| 2 |  |
1 |  |
 |
 |
----
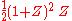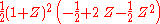For A=4 one obtains the 9/7-CDF-wavelet. One gets
, this polynomial has exactly one real root, thus it is the product of a linear factor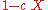 
and a quadratic factor. The coefficient c, which is the inverse of the root, has an approximate value of -1.4603482098.| A | QA(X) | qprim(X) | qdual(X) |
|---|---|---|---|
| 4 |  |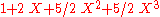
 |
 |
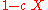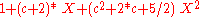For the coefficients of the centered scaling and wavelet sequences one gets numerical values in an implementation–friendly form
| k | Analysis lowpass filter (1/2 adual) |
Analysis highpass filter (bdual) |
Synthesis lowpass filter (aprim) |
Synthesis highpass filter (1/2 bprim) |
|---|---|---|---|---|
| -4 | 0.026748757411 | 0 | 0 | 0.026748757411 |
| -3 | -0.016864118443 | 0.091271763114 | -0.091271763114 | 0.016864118443 |
| -2 | -0.078223266529 | -0.057543526229 | -0.057543526229 | -0.078223266529 |
| -1 | 0.266864118443 | -0.591271763114 | 0.591271763114 | -0.266864118443 |
| 0 | 0.602949018236 | 1.11508705 | 1.11508705 | 0.602949018236 |
| 1 | 0.266864118443 | -0.591271763114 | 0.591271763114 | -0.266864118443 |
| 2 | -0.078223266529 | -0.057543526229 | -0.057543526229 | -0.078223266529 |
| 3 | -0.016864118443 | 0.091271763114 | -0.091271763114 | 0.016864118443 |
| 4 | 0.026748757411 | 0 | 0 | 0.026748757411 |
Numbering
There are two concurring numbering schemes for wavelets of the CDF family.- the number of smoothness factors of the lowpass filters, or equivalently the number of vanishing momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the highpass filters, e.g. 2,2 - the sizes of the lowpass filters, or equivalently the sizes of the highpass filters, e.g. 5,3
The first numbering was used in Daubechies' book Ten lectures on wavelets.
Neither of this numbering is unique. The number of vanishing moments does not tell about the chosen factorization. A filterbank with filter sizes 7 and 9 can have 6 and 2 vanishing moments when using the trivial factorization, or 4 and 4 vanishing moments as it is the case for the JPEG 2000 wavelet. The same wavelet may therefore be referred to as "CDF 9/7" (based on the filter sizes) or "biorthogonal 4.4" (based on the vanishing moments).
Lifting decomposition
For the trivially factorized filterbanks a lifting decompositionLifting scheme
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform.Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform....
can be explicitly given.
Even number of smoothness factors
Let
be the number of smoothness factors in the B-spline lowpass filter,which shall be even.
Then define recursively
The lifting filters are
Conclusively the interim results of the lifting are
which leads to
The filters
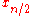and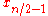 
constitute the CDF-n,0 filterbank.Odd number of smoothness factors
Now, let
be odd.Then define recursively
The lifting filters are
Conclusively the interim results of the lifting are
which leads to
where we neglect the translation and the constant factor.
The filters
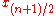and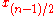 
constitute the CDF-n,1 filterbank.