Chaotic mixing
Encyclopedia
In chaos theory
and fluid dynamics
, chaotic mixing is a process
by which flow tracer
s develop into complex fractals under the action
of a time-varying fluid
flow.
The flow is characterized by an exponential growth of fluid filaments.
Even very simple flows, such as the blinking vortex,
or finitely resolved wind fields can generate exceptionally complex
patterns from initially simple tracer fields.
The phenomenon is still not well understood and is the subject
of much current research.
in the fluid is determined by the
following system of ordinary differential equation
s:
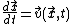
where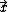
is the physical position, t is time, and
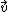is the fluid velocity as a function of
both position and time. If the flow is chaotic, then small initial errors in a
trajectory will diverge exponentially.
We are interested in calculating the stability—i.e., how fast do nearby
trajectories diverge? Suppose we make a small perturbation,
, then using a Taylor expansion, we get:
The Jacobi matrix of the velocity field,
,
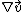provides information about the local rate of divergence of
nearby trajectories or the local rate of stretching of
Lagrangian space.
The rate of change of the error vectors is given approximately as:
We define the matrix H such that:
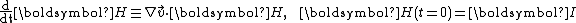
where I is the identity matrix. It follows that:
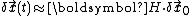
The Lyapunov exponents are defined as the time average of the logarithms
of the lengths of the principal components of the vector H
in the limit as t approaches infinity:
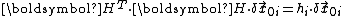
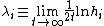
where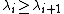
is the ith Lyapunov exponent
of the system, while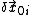
is the ith principal component
of the matrix H.
If we start with a set of orthonormal initial error vectors,
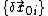then the matrix H will map them to a set
of final orthogonal error vectors of length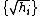
.
The action of the system maps an infinitesimal sphere of
inititial points to an ellipsoid whose major axis is given by the
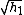while the minor axis is given by 
,
where N is the number of dimensions.
This definition of Lyapunov exponent
s is both more elegant and more appropriate
to real-world, continuous-time dynamical systems than the more usual definition based
on discrete function maps.
Chaos
is defined as at least one positive Lyapunov exponent.
If there is any significant difference between the Lyapunov exponents then as an error vector evolves forward in time, any displacement in the direction of largest growth will tend to be magnified. Thus:
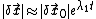
where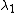
is the largest Lyapunov exponent. In fact, the Lyapunov exponent is often somewhat incorrectly defined in this way.
is another useful method for characterizing chaotic mixing.
In chaotic flows, advected contours will grow exponentially over time.
The figure above shows the frame-by-frame evolution of a contour advected over
several days. The figure to the right shows the length of this contour
as a function of time.
The link between exponential contour growth and positive Lyapunov exponents is
easy to see. The rate of contour growth is given as:
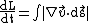
where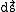
is the path
and the integral is performed over the length of the contour.
Contour growth rates will approximate the average of the large Lyapunov exponents:
,"
tracers advected in chaotic flows will develop into complex fractals.
The fractal dimension
of a single contour will be between 1 and 2.
Exponential growth ensures that the contour, in the limit of very
long time integration, becomes fractal.
Fractals composed of a single curve are infinitely long and when
formed iteratively, have an exponential growth rate, just like an
advected contour.
The Koch Snowflake
, for instance, grows at a rate of 4/3 per iteration.
The figure below shows the fractal dimension
of an advected contour as a function
of time, measured in four different ways. A good method of measuring the
fractal dimension of an advected contour is the uncertainty exponent
.
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, chaotic mixing is a process
by which flow tracer
Flow tracer
thumb|right|300px|On May 2, [[2001]], the Moderate-resolution Imaging Spectroradiometer obtained this spectacular image of the [[Atlantic Ocean]]'s [[Gulf Stream]]. The [[false color]]s in the image represent "[[brightness temperature]]" observed at the top of the [[atmosphere]]...
s develop into complex fractals under the action
of a time-varying fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
flow.
The flow is characterized by an exponential growth of fluid filaments.
Even very simple flows, such as the blinking vortex,
or finitely resolved wind fields can generate exceptionally complex
patterns from initially simple tracer fields.
The phenomenon is still not well understood and is the subject
of much current research.
Lyapunov exponents
A trajectoryTrajectory (fluid mechanics)
In fluid mechanics, meteorology and oceanography, a trajectory traces the motion of a single point, often called a parcel, in the flow.Trajectories are useful for tracking atmospheric contaminants, such as smoke plumes,...
in the fluid is determined by the
following system of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s:
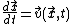
where
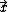is the physical position, t is time, and 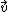is the fluid velocity as a function ofboth position and time. If the flow is chaotic, then small initial errors in a
trajectory will diverge exponentially.
We are interested in calculating the stability—i.e., how fast do nearby
trajectories diverge? Suppose we make a small perturbation,
, then using a Taylor expansion, we get:The Jacobi matrix of the velocity field,
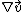,provides information about the local rate of divergence of
nearby trajectories or the local rate of stretching of
Lagrangian space.
The rate of change of the error vectors is given approximately as:
We define the matrix H such that:
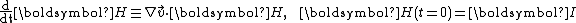
where I is the identity matrix. It follows that:
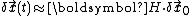
The Lyapunov exponents are defined as the time average of the logarithms
of the lengths of the principal components of the vector H
in the limit as t approaches infinity:
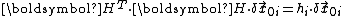
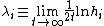
where
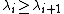is the ith Lyapunov exponentLyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
of the system, while
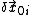is the ith principal componentof the matrix H.
If we start with a set of orthonormal initial error vectors,
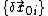then the matrix H will map them to a setof final orthogonal error vectors of length
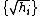.The action of the system maps an infinitesimal sphere of
inititial points to an ellipsoid whose major axis is given by the
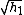while the minor axis is given by ,where N is the number of dimensions.
This definition of Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
s is both more elegant and more appropriate
to real-world, continuous-time dynamical systems than the more usual definition based
on discrete function maps.
Chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
is defined as at least one positive Lyapunov exponent.
If there is any significant difference between the Lyapunov exponents then as an error vector evolves forward in time, any displacement in the direction of largest growth will tend to be magnified. Thus:
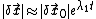
where
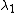is the largest Lyapunov exponent. In fact, the Lyapunov exponent is often somewhat incorrectly defined in this way.Contour advection
Contour advectionContour advection
Contour advection is a Lagrangian methodof simulating the evolution of one or more contours or isolines ofa tracer as it is stirred by a moving fluid....
is another useful method for characterizing chaotic mixing.
In chaotic flows, advected contours will grow exponentially over time.
The figure above shows the frame-by-frame evolution of a contour advected over
several days. The figure to the right shows the length of this contour
as a function of time.
The link between exponential contour growth and positive Lyapunov exponents is
easy to see. The rate of contour growth is given as:
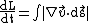
where
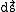is the pathand the integral is performed over the length of the contour.
Contour growth rates will approximate the average of the large Lyapunov exponents:
Fractal dimension
Through a continual process of stretching and folding, much like in a "baker's mapBaker's map
In dynamical systems theory, the baker's map is a chaotic map from the unit square into itself. It is named after a kneading operation that bakers apply to dough: the dough is cut in half, and the two halves are stacked on one-another, and compressed...
,"
tracers advected in chaotic flows will develop into complex fractals.
The fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
of a single contour will be between 1 and 2.
Exponential growth ensures that the contour, in the limit of very
long time integration, becomes fractal.
Fractals composed of a single curve are infinitely long and when
formed iteratively, have an exponential growth rate, just like an
advected contour.
The Koch Snowflake
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
, for instance, grows at a rate of 4/3 per iteration.
The figure below shows the fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
of an advected contour as a function
of time, measured in four different ways. A good method of measuring the
fractal dimension of an advected contour is the uncertainty exponent
Uncertainty exponent
In mathematics, the uncertainty exponent is a method of measuring the fractal dimension of a basin boundary. In a chaotic scattering system, the...
.