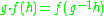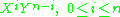Borel–Weil theorem
Encyclopedia
In mathematics
, in the field of representation theory
, the Borel–Weil theorem, named after Armand Borel
and André Weil
, provides a concrete model for irreducible representations of compact Lie groups and complex semisimple Lie groups. These representations are realized in the spaces of global sections of holomorphic line bundles on the flag manifold
of the group. Its generalization to higher cohomology spaces is called the Borel–Weil–Bott theorem.
complex semisimple Lie group, B its Borel subgroup
, and X=G/B the flag variety. In this picture, X is a complex manifold and a nonsingular algebraic G-variety. The flag variety can also be described as a compact homogeneous space
K/T, where T=K∩B is a (compact) Cartan subgroup
of K. An integral weight λ
determines a G-equivariant holomorphic line bundle Lλ on X and the group G acts on its space of global sections,
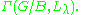
The Borel–Weil theorem states that if λ is a dominant integral weight then this representation is an irreducible highest weight representation of G with highest weight λ. Its restriction to K is an irreducible unitary representation of K with highest weight λ, and each irreducible unitary representations of K is obtained in this way for a unique value of λ.

for all g∈G and b∈B.
The action of G on these sections is given by
for g,h∈G.
SL(2,C), with a Borel subgroup consisting of upper triangular matrices with determinant one. Integral weights for G may be identified with integer
s, with dominant weights corresponding to nonnegative integers, and the corresponding characters χn of B have the form
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, the Borel–Weil theorem, named after Armand Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
and André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, provides a concrete model for irreducible representations of compact Lie groups and complex semisimple Lie groups. These representations are realized in the spaces of global sections of holomorphic line bundles on the flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
of the group. Its generalization to higher cohomology spaces is called the Borel–Weil–Bott theorem.
Statement of the theorem
The theorem can be stated either for a complex semisimple Lie group G or for its compact form K. Let G be a connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
complex semisimple Lie group, B its Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
, and X=G/B the flag variety. In this picture, X is a complex manifold and a nonsingular algebraic G-variety. The flag variety can also be described as a compact homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
K/T, where T=K∩B is a (compact) Cartan subgroup
Cartan subgroup
In mathematics, a Cartan subgroup of a Lie group or algebraic group G is one of the subgroups whose Lie algebrais a Cartan subalgebra. The dimension of a Cartan subgroup, and therefore of a Cartan subalgebra, is the rank of G.-Conventions:...
of K. An integral weight λ
determines a G-equivariant holomorphic line bundle Lλ on X and the group G acts on its space of global sections,
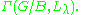
The Borel–Weil theorem states that if λ is a dominant integral weight then this representation is an irreducible highest weight representation of G with highest weight λ. Its restriction to K is an irreducible unitary representation of K with highest weight λ, and each irreducible unitary representations of K is obtained in this way for a unique value of λ.
Concrete description
The weight λ gives rise to a character (one-dimensional representation) of the Borel subgroup B, which is denoted χλ. Holomorphic sections of the holomorphic line bundle Lλ over G/B may be described more concretely as holomorphic maps
for all g∈G and b∈B.
The action of G on these sections is given by
for g,h∈G.
Example
Let G be the complex special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,C), with a Borel subgroup consisting of upper triangular matrices with determinant one. Integral weights for G may be identified with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, with dominant weights corresponding to nonnegative integers, and the corresponding characters χn of B have the form
-
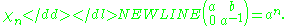
The flag variety G/B may be identified with the complex projective line P1 with homogeneous coordinates X, Y and the space of the global sections of the line bundle Ln is identified with the space of homogeneous polynomials of degree n on C2. For n≥0, this space has dimension n+1 and forms an irreducible representation under the standard action of G on the polynomial algebra C[X,Y]. Weight vectors are given by monomials
of weights 2i−n, and the highest weight vector Xn has weight n.
History
The theorem dates back to the early 1950s and can be found in and . -