
Borel determinacy theorem
Encyclopedia
In descriptive set theory
, the Borel determinacy theorem states that any Gale-Stewart game whose winning set is a Borel set
is determined
, meaning that one of the two players will have a winning strategy for the game. It was proved by Donald A. Martin
in 1975. The theorem is applied in descriptive set theory to show that Borel sets in Polish spaces have regularity properties such as the perfect set property
and the property of Baire.
The theorem is also known for its metamathematical
properties. In 1971, before the theorem was proved, Harvey Friedman
showed that any proof of the theorem in Zermelo-Fraenkel set theory must make repeated use of the axiom of replacement. Later results showed that stronger determinacy theorems cannot be proven in Zermelo-Fraenkel set theory, although they are relatively consistent with it.
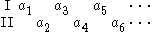
The play continues without end, so that a single play of the game determines an infinite sequence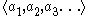 of elements of A. The set of all such sequences is denoted Aω. The players are aware, from the beginning of the game, of a fixed payoff set that will determine who wins. The payoff set is a subset
of elements of A. The set of all such sequences is denoted Aω. The players are aware, from the beginning of the game, of a fixed payoff set that will determine who wins. The payoff set is a subset
of Aω. If the infinite sequence created by a play of the game is in the payoff set, then player I wins. Otherwise, player II wins; there are no ties.
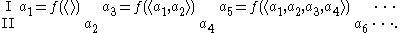
A winning strategy for player II is a function g that takes odd-length sequences of elements of A and returns elements of A, such that player II will win every play of the form
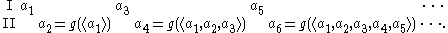
At most one player can have a winning strategy; if both players had winning strategies, and played the strategies against each other, only one of the two strategies could win that play of the game. If one of the players has a winning strategy for a particular payoff set, that payoff set is said to be determined.
, and Aω endowed with the resulting product topology
, where Aω is viewed as a countably infinite topological product of A with itself. In particular, when A is the set {0,1}, the topology defined on Aω is exactly the ordinary topology on Cantor space
, and when A is the set of natural numbers, it is the ordinary topology on Baire space
.
The set Aω can be viewed as the set of paths through a certain tree, which leads to a second characterization of its topology. The tree consists of all finite sequences of elements of A, and the children of a particular node σ of the tree are exactly the sequences that extend σ by one element. Thus if A = { 0, 1 }, the first level of the tree consists of the sequences ⟨ 0 ⟩ and ⟨ 1 ⟩; the second level consists of the four sequences ⟨ 0, 0 ⟩, ⟨ 0, 1 ⟩, ⟨ 1, 0 ⟩, ⟨ 1, 1 ⟩; and so on. For each of the finite sequences σ in the tree, the set of all elements of Aω that begin with σ is a basic open set in the topology on A. The open set
s of Aω are precisely the sets expressible as unions of these basic open sets. The closed set
s, as usual, are those whose complement is open.
The Borel set
s of Aω are the smallest class of subsets of Aω that includes the open sets and is closed under complement and countable union. That is, the Borel sets are the smallest σ-algebra
of subsets of Aω containing all the open sets. The Borel sets are classified in the Borel hierarchy
based on how many times the operations of complement and countable union are required to produce them from open sets.
or closed
subset of Aω then the Gale–Stewart game with that payoff set is always determined. Over the next twenty years, this was extended to slightly higher levels of the Borel hierarchy
through ever more complicated proofs. This led to the question of whether the game must be determined whenever the payoff set is a Borel subset
of Aω. It was known that, using the axiom of choice, it is possible to construct a subset of {0,1}ω that is not determined (Kechris 1995, p. 139).
Harvey Friedman
(1971) proved that that any proof that all Borel subsets of Cantor space ({0,1}ω ) were determined would require repeated use of the axiom of replacement, an axiom not typically required to prove theorems about "small" objects such as Cantor space.
(1975) proved that for any set A, all Borel subsets of Aω are determined. Because the original proof was quite complicated, Martin published a shorter proof in 1982 that did not require as much technical machinery. In his review of Martin's paper, Drake describes the second proof as "surprisingly straightforward."
The field of descriptive set theory
studies properties of Polish space
s (essentially, complete separable metric spaces). The Borel determinacy theorem has been used to establish many properties of Borel subsets of these spaces. For example, all Borel subsets of Polish spaces have the perfect set property
and the property of Baire.
properties as well as its consequences in descriptive set theory.
Determinacy of closed sets of Aω for arbitrary A is equivalent to the axiom of choice over ZF (Kechris 1995, p. 139). When working in set-theoretical systems where the axiom of choice is not assumed, this can be circumvented by considering generalized strategies known as quasistrategies (Kechris 1995, p. 139) or by only considering games where A is the set of natural numbers, as in the axiom of determinacy
.
Zermelo set theory (Z) is Zermelo-Fraenkel set theory without the axiom of replacement. It differs from ZF in that Z does not prove that the powerset operation can be iterated uncountably many times beginning with an arbitrary set. In particular, Vω + ω, a particular countable level of the cumulative hierarchy, is a model of Zermelo set theory. The axiom of replacement, on the other hand, is only satisfied by Vκ for significantly larger values of κ, such as when κ is a strongly inaccessible cardinal. Friedman's theorem of 1971 showed that there is a model of Zermelo set theory (with the axiom of choice) in which Borel determinacy fails, and thus Zermelo set theory cannot prove the Borel determinacy theorem.
The axiom of projective determinacy
states that all projective subsets of a Polish space are determined. It is known to be unprovable in ZFC but relatively consistent with it and implied by certain large cardinal axioms. The existence of a measurable cardinal
is enough to imply over ZFC that all analytic subsets
of Polish spaces are determined.
The axiom of determinacy
states that all subsets of all Polish spaces are determined. It is inconsistent with ZFC but equiconsistent with certain large cardinal axioms.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, the Borel determinacy theorem states that any Gale-Stewart game whose winning set is a Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
is determined
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
, meaning that one of the two players will have a winning strategy for the game. It was proved by Donald A. Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
in 1975. The theorem is applied in descriptive set theory to show that Borel sets in Polish spaces have regularity properties such as the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
and the property of Baire.
The theorem is also known for its metamathematical
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
properties. In 1971, before the theorem was proved, Harvey Friedman
Harvey Friedman
Harvey Friedman is a mathematical logician at Ohio State University in Columbus, Ohio. He is noted especially for his work on reverse mathematics, a project intended to derive the axioms of mathematics from the theorems considered to be necessary...
showed that any proof of the theorem in Zermelo-Fraenkel set theory must make repeated use of the axiom of replacement. Later results showed that stronger determinacy theorems cannot be proven in Zermelo-Fraenkel set theory, although they are relatively consistent with it.
Gale–Stewart games
A Gale–Stewart game is a two-player game of perfect information. The game is defined using a set A, and is denoted GA. The two players alternate turns, and each player is aware of all moves before making the next one. On each turn, each player chooses a single element of A to play. The same element may be chosen more than once without restriction. The game can be visualized through the following diagram, in which the moves are made from left to right, with the moves of player I above and the moves of player II below.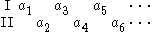
The play continues without end, so that a single play of the game determines an infinite sequence
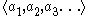 of elements of A. The set of all such sequences is denoted Aω. The players are aware, from the beginning of the game, of a fixed payoff set that will determine who wins. The payoff set is a subset
of elements of A. The set of all such sequences is denoted Aω. The players are aware, from the beginning of the game, of a fixed payoff set that will determine who wins. The payoff set is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Aω. If the infinite sequence created by a play of the game is in the payoff set, then player I wins. Otherwise, player II wins; there are no ties.
Winning strategies
A winning strategy for a player is a function that tells the player what move to make from any position in the game, such that if the player follows the function he or she will surely win. More specifically, a winning strategy for player I is a function f that takes as input sequences of elements of A of even length and returns an element of A, such that player I will win every play of the form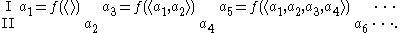
A winning strategy for player II is a function g that takes odd-length sequences of elements of A and returns elements of A, such that player II will win every play of the form
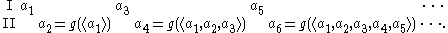
At most one player can have a winning strategy; if both players had winning strategies, and played the strategies against each other, only one of the two strategies could win that play of the game. If one of the players has a winning strategy for a particular payoff set, that payoff set is said to be determined.
Topology
For a given set A, whether a subset of Aω will be determined depends to some extent on its topological structure. For the purposes of Gale–Stewart games, the set A is endowed with the discrete topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and Aω endowed with the resulting product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, where Aω is viewed as a countably infinite topological product of A with itself. In particular, when A is the set {0,1}, the topology defined on Aω is exactly the ordinary topology on Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
, and when A is the set of natural numbers, it is the ordinary topology on Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
.
The set Aω can be viewed as the set of paths through a certain tree, which leads to a second characterization of its topology. The tree consists of all finite sequences of elements of A, and the children of a particular node σ of the tree are exactly the sequences that extend σ by one element. Thus if A = { 0, 1 }, the first level of the tree consists of the sequences ⟨ 0 ⟩ and ⟨ 1 ⟩; the second level consists of the four sequences ⟨ 0, 0 ⟩, ⟨ 0, 1 ⟩, ⟨ 1, 0 ⟩, ⟨ 1, 1 ⟩; and so on. For each of the finite sequences σ in the tree, the set of all elements of Aω that begin with σ is a basic open set in the topology on A. The open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of Aω are precisely the sets expressible as unions of these basic open sets. The closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s, as usual, are those whose complement is open.
The Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of Aω are the smallest class of subsets of Aω that includes the open sets and is closed under complement and countable union. That is, the Borel sets are the smallest σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
of subsets of Aω containing all the open sets. The Borel sets are classified in the Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
based on how many times the operations of complement and countable union are required to produce them from open sets.
Previous results
Gale and Stewart (1953) proved that if the payoff set is an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
or closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subset of Aω then the Gale–Stewart game with that payoff set is always determined. Over the next twenty years, this was extended to slightly higher levels of the Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
through ever more complicated proofs. This led to the question of whether the game must be determined whenever the payoff set is a Borel subset
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of Aω. It was known that, using the axiom of choice, it is possible to construct a subset of {0,1}ω that is not determined (Kechris 1995, p. 139).
Harvey Friedman
Harvey Friedman
Harvey Friedman is a mathematical logician at Ohio State University in Columbus, Ohio. He is noted especially for his work on reverse mathematics, a project intended to derive the axioms of mathematics from the theorems considered to be necessary...
(1971) proved that that any proof that all Borel subsets of Cantor space ({0,1}ω ) were determined would require repeated use of the axiom of replacement, an axiom not typically required to prove theorems about "small" objects such as Cantor space.
Borel determinacy
Donald A. MartinDonald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
(1975) proved that for any set A, all Borel subsets of Aω are determined. Because the original proof was quite complicated, Martin published a shorter proof in 1982 that did not require as much technical machinery. In his review of Martin's paper, Drake describes the second proof as "surprisingly straightforward."
The field of descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
studies properties of Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
s (essentially, complete separable metric spaces). The Borel determinacy theorem has been used to establish many properties of Borel subsets of these spaces. For example, all Borel subsets of Polish spaces have the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
and the property of Baire.
Set-theoretic aspects
The Borel determinacy theorem is of interest for its metamethematicalMetamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
properties as well as its consequences in descriptive set theory.
Determinacy of closed sets of Aω for arbitrary A is equivalent to the axiom of choice over ZF (Kechris 1995, p. 139). When working in set-theoretical systems where the axiom of choice is not assumed, this can be circumvented by considering generalized strategies known as quasistrategies (Kechris 1995, p. 139) or by only considering games where A is the set of natural numbers, as in the axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
.
Zermelo set theory (Z) is Zermelo-Fraenkel set theory without the axiom of replacement. It differs from ZF in that Z does not prove that the powerset operation can be iterated uncountably many times beginning with an arbitrary set. In particular, Vω + ω, a particular countable level of the cumulative hierarchy, is a model of Zermelo set theory. The axiom of replacement, on the other hand, is only satisfied by Vκ for significantly larger values of κ, such as when κ is a strongly inaccessible cardinal. Friedman's theorem of 1971 showed that there is a model of Zermelo set theory (with the axiom of choice) in which Borel determinacy fails, and thus Zermelo set theory cannot prove the Borel determinacy theorem.
Stronger forms of determinacy
Several set-theoretic principles about determinacy stronger than Borel determinacy are studied in descriptive set theory. They are closely related to large cardinal axioms.The axiom of projective determinacy
Axiom of projective determinacy
In mathematical logic, projective determinacy is the special case of the axiom of determinacy applying only to projective sets.The axiom of projective determinacy, abbreviated PD, states that for any two-player game of perfect information of length ω in which the players play natural numbers, if...
states that all projective subsets of a Polish space are determined. It is known to be unprovable in ZFC but relatively consistent with it and implied by certain large cardinal axioms. The existence of a measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
is enough to imply over ZFC that all analytic subsets
Analytic set
In descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
of Polish spaces are determined.
The axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
states that all subsets of all Polish spaces are determined. It is inconsistent with ZFC but equiconsistent with certain large cardinal axioms.
External links
- Borel determinacy and metamathematics. Ross Bryant. Master's thesis, University of North Texas, 2001.

