
Bloch equations
Encyclopedia
In physics and chemistry, specifically in NMR
(nuclear magnetic resonance) or MRI (magnetic resonance imaging), or ESR (electron spin resonance) the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = (Mx, My, Mz) as a function of time when relaxation times
T1 and T2 are present. These are phenomenological
equations that were introduced by Felix Bloch
in 1946.
Sometimes they are called the equations of motion of nuclear magnetization.



where γ is the gyromagnetic ratio and B(t) = (Bx(t), By(t), B0 + ΔBz(t)) is the magnetic field
experienced by the nuclei.
The z component of the magnetic field B is sometimes composed of two terms:
M(t) × B(t) is the cross product
of these two vectors.
M0 is the steady state nuclear magnetization (that is, for example, when t → ∞); it is in the z direction.
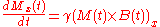

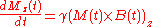
or, in vector notation:
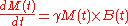
This is the equation for Larmor precession
of the nuclear magnetization M in an external magnetic field B.
The relaxation terms,
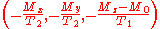
represent an established physical process of transverse and longitudinal relaxation of nuclear magnetization M.
.
Bloch equations are macroscopic: they describe the equations of motion of macroscopic nuclear magnetization that can be obtained by summing up all nuclear magnetic moment in the sample.
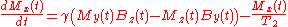

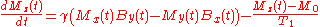
The above form is further simplified assuming

where i = √(-1). After some algebra one obtains:
 .
.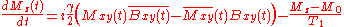
where
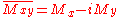 .
.
The real and imaginary parts of Mxy correspond to Mx and My respectively.
Mxy is sometimes called transverse nuclear magnetization.
Then the Bloch equations are simplified to:
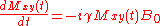 ,
,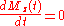 .
.
These are two (not coupled) linear differential equations. Their solution is:
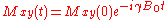 ,
,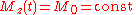 .
.
Thus the transverse magnetization, Mxy, rotates around the z axis with angular frequency
ω0 = γB0 in clockwise direction (this is due to the negative sign in the exponent).
The longitudinal magnetization, Mz remains constant in time. This is also how the transverse magnetization appears to an observer in the laboratory frame of reference (that is to a stationary observer).
Mxy(t) is translated in the following way into observable quantities of Mx(t) and My(t): Since

then
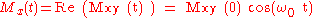 ,
,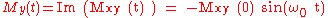 ,
,
where Re(z) and Im(z) are functions that return the real and imaginary part of complex number z. In this calculation it was assumed that Mxy(0) is a real number.
clockwise direction with angular frequency ω0 , the transverse magnetization Mxy would appear to him stationary.
This can be expressed mathematically in the following way:
Obviously:
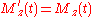 .
.
What is Mxy′(t)? Expressing the argument at the beginning of this section in a mathematical way:
 .
.
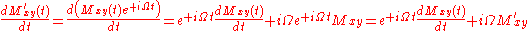
Substitute from the Bloch equation in laboratory frame of reference:

But by assumption in the previous section: Bz′(t) = Bz(t) = B0 + ΔBz(t). Substituting into the equation above:
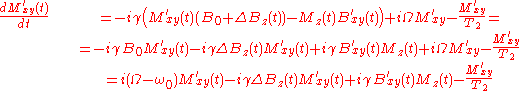
This is the meaning of terms on the right hand side of this equation:
Then in the rotating frame of reference, the equation of motion for the transverse nuclear magnetization, Mxy'(t) simplifies to:

This is a linear ordinary differential equation and its solution is
 .
.
where Mxy'(0) is the transverse nuclear magnetization in the rotating frame at time t = 0. This is the initial condition for the differential equation.
Note that when the rotating frame of reference rotates exactly at the Larmor frequency (this is the physical meaning of the above assumption Ω = ω0), the vector of transverse nuclear magnetization, Mxy(t) appears to be stationary.
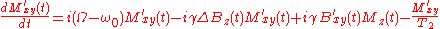
NMR
NMR may refer to:Applications of Nuclear Magnetic Resonance:* Nuclear magnetic resonance* NMR spectroscopy* Solid-state nuclear magnetic resonance* Protein nuclear magnetic resonance spectroscopy* Proton NMR* Carbon-13 NMR...
(nuclear magnetic resonance) or MRI (magnetic resonance imaging), or ESR (electron spin resonance) the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = (Mx, My, Mz) as a function of time when relaxation times
Relaxation (NMR)
In nuclear magnetic resonance spectroscopy and magnetic resonance imaging the term relaxation describes several processes by which nuclear magnetization prepared in a non-equilibrium state return to the equilibrium distribution. In other words, relaxation describes how fast spins "forget" the...
T1 and T2 are present. These are phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
equations that were introduced by Felix Bloch
Felix Bloch
Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...
in 1946.
Sometimes they are called the equations of motion of nuclear magnetization.
Bloch equations in laboratory (stationary) frame of reference
Let M(t) = (Mx(t), My(t), Mz(t)) be the nuclear magnetization. Then the Bloch equations read:


where γ is the gyromagnetic ratio and B(t) = (Bx(t), By(t), B0 + ΔBz(t)) is the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
experienced by the nuclei.
The z component of the magnetic field B is sometimes composed of two terms:
- one, B0, is constant in time,
- the other one, ΔBz(t), may be time dependent. It is present in magnetic resonance imaging and helps with the spatial decoding of the NMR signal.
M(t) × B(t) is the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of these two vectors.
M0 is the steady state nuclear magnetization (that is, for example, when t → ∞); it is in the z direction.
Physical background
With no relaxation (that is both T1 and T2 → ∞) the above equations simplify to: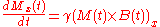

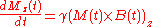
or, in vector notation:
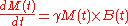
This is the equation for Larmor precession
Larmor precession
In physics, Larmor precession is the precession of the magnetic moments of electrons, atomic nuclei, and atoms about an external magnetic field...
of the nuclear magnetization M in an external magnetic field B.
The relaxation terms,
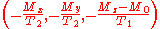
represent an established physical process of transverse and longitudinal relaxation of nuclear magnetization M.
Bloch equations are macroscopic equations
These equations are not microscopic: they do not describe the equation of motion of individual nuclear magnetic moments. These are governed and described by laws of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Bloch equations are macroscopic: they describe the equations of motion of macroscopic nuclear magnetization that can be obtained by summing up all nuclear magnetic moment in the sample.
Alternative forms of Bloch equations
Opening the vector product brackets in the Bloch equations leads to: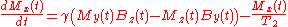

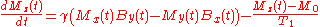
The above form is further simplified assuming

where i = √(-1). After some algebra one obtains:
 .
.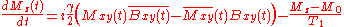
where
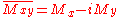 .
.The real and imaginary parts of Mxy correspond to Mx and My respectively.
Mxy is sometimes called transverse nuclear magnetization.
Bloch equations in rotating frame of reference
In a rotating frame of reference, it is easier to understand the behaviour of the nuclear magnetization M. This is the motivation:Solution of Bloch equations with T1, T2 → ∞
Assume that:- at t = 0 the transverse nuclear magnetization Mxy(0) experiences a constant magnetic field B(t) = (0, 0, B0);
- B0 is positive;
- there are no longitudinal and transverse relaxations (that is T1 and T2 → ∞).
Then the Bloch equations are simplified to:
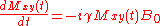 ,
,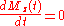 .
.These are two (not coupled) linear differential equations. Their solution is:
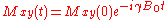 ,
,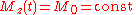 .
. Thus the transverse magnetization, Mxy, rotates around the z axis with angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω0 = γB0 in clockwise direction (this is due to the negative sign in the exponent).
The longitudinal magnetization, Mz remains constant in time. This is also how the transverse magnetization appears to an observer in the laboratory frame of reference (that is to a stationary observer).
Mxy(t) is translated in the following way into observable quantities of Mx(t) and My(t): Since

then
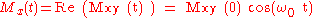 ,
,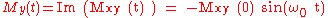 ,
,where Re(z) and Im(z) are functions that return the real and imaginary part of complex number z. In this calculation it was assumed that Mxy(0) is a real number.
Transformation to rotating frame of reference
This is the conclusion of the previous section: in a constant magnetic field B0 along z axis the transverse magnetization Mxy rotates around this axis in clockwise direction with angular frequency ω0. If the observer were rotating around the same axis in clockwise direction with angular frequency Ω, Mxy it would appear to him rotating with angular frequency ω0 - Ω. Specifically, if the observer were rotating around the same axis inclockwise direction with angular frequency ω0 , the transverse magnetization Mxy would appear to him stationary.
This can be expressed mathematically in the following way:
- Let (x, y, z) the Cartesian coordinate system of the laboratory (or stationary) frame of reference, and
- (x′, y′, z′) be a Cartesian coordinate system that is rotating around the z axis of the laboratory frame of reference with angular frequency Ω. This is called the rotating frame of reference. Physical variables in this frame of reference will be denoted by a prime.
Obviously:
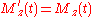 .
.What is Mxy′(t)? Expressing the argument at the beginning of this section in a mathematical way:
 .
.Equation of motion of transverse magnetization in rotating frame of reference (outline)
What is the equations of motion of Mxy′(t)?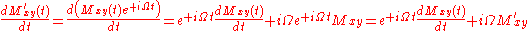
Substitute from the Bloch equation in laboratory frame of reference:

But by assumption in the previous section: Bz′(t) = Bz(t) = B0 + ΔBz(t). Substituting into the equation above:
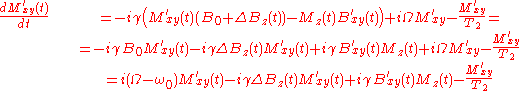
This is the meaning of terms on the right hand side of this equation:
- i (Ω - ω) Mxy′(t) is the Larmor term in the frame of reference rotating with angular frequency Ω. Note that it becomes zero when Ω = ω0.
- The -i γ ΔBz(t) Mxy′(t) term describes the effect of magnetic field inhomogeneity (as expressed by ΔBz(t)) on the transverse nuclear magnetization; it is used to explain T2*. It is also the term that is behind MRI: it is generated by the gradient coil system.
- The i γ ΔBxy′(t) Mz(t) describes the effect of RF field (the ΔBxy′(t) factor) on nuclear magnetization. For an example see below.
- - Mxy′(t) / T2 describes the loss of coherency of transverse magnetization.
Relaxation of transverse nuclear magnetization Mxy
Assume that:- The nuclear magnetization is exposed to constant external magnetic field in the z direction Bz′(t) = Bz(t) = B0. Thus ω0 = γB0 and ΔBz(t) = 0.
- There is no RF, that is Bxy' = 0.
- The rotating frame of reference rotates with an angular frequency Ω = ω0.
Then in the rotating frame of reference, the equation of motion for the transverse nuclear magnetization, Mxy'(t) simplifies to:

This is a linear ordinary differential equation and its solution is
 .
.where Mxy'(0) is the transverse nuclear magnetization in the rotating frame at time t = 0. This is the initial condition for the differential equation.
Note that when the rotating frame of reference rotates exactly at the Larmor frequency (this is the physical meaning of the above assumption Ω = ω0), the vector of transverse nuclear magnetization, Mxy(t) appears to be stationary.
90 and 180° RF pulses
Assume that:- Nuclear magnetization is exposed to constant external magnetic field in z direction Bz′(t) = Bz(t) = B0. Thus ω0 = γB0 and ΔBz(t) = 0.
- At t = 0 an RF pulse of constant amplitude and frequency ω0 is applied.
- The rotating frame of reference rotates with an angular frequency Ω = ω0.
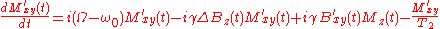
Relaxation of longitudinal nuclear magnetization Mz
See also
- The Bloch–Torrey equation is a generalization of the Bloch equations, which includes added terms due to the transfer of magnetization by diffusion.
Further reading
- Charles KittelCharles KittelCharles Kittel is an American physicist. He was a Professor at University of California, Berkeley from 1951 and has been Professor Emeritus since 1978.- Life and work :...
, Introduction to Solid State Physics, John Wiley & Sons, 8th edition (2004), ISBN 978-0471415268. Chapter 13 is on Magnetic Resonance.

