
Birnbaum–Orlicz space
Encyclopedia
In the mathematical analysis
, and especially in real
and harmonic analysis
, a Birnbaum–Orlicz space is a type of function space which generalizes the Lp spaces
. Like the Lp spaces, they are Banach space
s. The spaces are named for Władysław Orlicz and Zygmunt William Birnbaum, who first defined them in 1931.
Besides the Lp spaces, a variety of function spaces arising naturally in analysis are Birnbaum–Orlicz spaces. One such space L log+ L, which arises in the study of Hardy–Littlewood maximal functions, consists of measurable functions f such that the integral
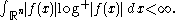
Here log+ is the positive part of the logarithm. Also included in the class of Birnbaum–Orlicz spaces are many of the most important Sobolev space
s.
such that

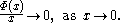
Let be the space of measurable functions f : X → R such that the integral
be the space of measurable functions f : X → R such that the integral
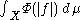
is finite, where as usual functions that agree almost everywhere
are identified.
This may not be a vector space (it may fail to be closed under scalar multiplication). The vector space of functions spanned by is the Birnbaum–Orlicz space, denoted
is the Birnbaum–Orlicz space, denoted 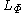 .
.
To define a norm on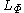 , let Ψ be the Young complement of Φ; that is,
, let Ψ be the Young complement of Φ; that is,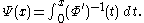
Note that Young's inequality
holds: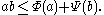
The norm is then given by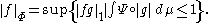
Furthermore, the space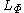 is precisely the space of measurable functions for which this norm is finite.
is precisely the space of measurable functions for which this norm is finite.
An equivalent norm is defined on LΦ by
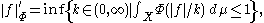
and likewise LΦ(μ) is the space of all measurable functions for which this norm is finite.
s are embedded in Orlicz spaces: for open
open
and bounded
with Lipschitz boundary
 ,
,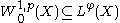
for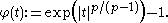
This is the analytical content of the Trudinger inequality: For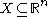 open and bounded with Lipschitz boundary
open and bounded with Lipschitz boundary 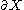 , consider the space
, consider the space 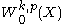 ,
, 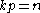 . There exist constants
. There exist constants 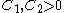 such that
such that
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, and especially in real
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, a Birnbaum–Orlicz space is a type of function space which generalizes the Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Like the Lp spaces, they are Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. The spaces are named for Władysław Orlicz and Zygmunt William Birnbaum, who first defined them in 1931.
Besides the Lp spaces, a variety of function spaces arising naturally in analysis are Birnbaum–Orlicz spaces. One such space L log+ L, which arises in the study of Hardy–Littlewood maximal functions, consists of measurable functions f such that the integral
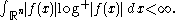
Here log+ is the positive part of the logarithm. Also included in the class of Birnbaum–Orlicz spaces are many of the most important Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s.
Formal definition
Suppose that μ is a σ-finite measure on a set X, and Φ : [0, ∞) → [0, ∞) is a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
such that

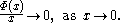
Let
 be the space of measurable functions f : X → R such that the integral
be the space of measurable functions f : X → R such that the integral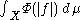
is finite, where as usual functions that agree almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
are identified.
This may not be a vector space (it may fail to be closed under scalar multiplication). The vector space of functions spanned by
 is the Birnbaum–Orlicz space, denoted
is the Birnbaum–Orlicz space, denoted 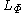 .
.To define a norm on
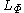 , let Ψ be the Young complement of Φ; that is,
, let Ψ be the Young complement of Φ; that is,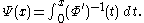
Note that Young's inequality
Young's inequality
In mathematics, the term Young's inequality is used for two inequalities: one about the product of two numbers, and one about the convolution of two functions. They are named for William Henry Young....
holds:
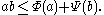
The norm is then given by
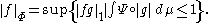
Furthermore, the space
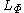 is precisely the space of measurable functions for which this norm is finite.
is precisely the space of measurable functions for which this norm is finite.An equivalent norm is defined on LΦ by
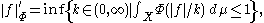
and likewise LΦ(μ) is the space of all measurable functions for which this norm is finite.
Properties
- Orlicz spaces generalize Lp spaces in the sense that if
 , then
, then 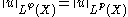 , so
, so 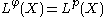 .
. - The Orlicz space
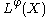 is a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
— a completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
normed vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
Relations to Sobolev spaces
Certain Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s are embedded in Orlicz spaces: for
 open
openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
with Lipschitz boundary
Lipschitz domain
In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
 ,
,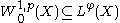
for
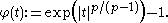
This is the analytical content of the Trudinger inequality: For
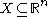 open and bounded with Lipschitz boundary
open and bounded with Lipschitz boundary 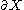 , consider the space
, consider the space 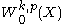 ,
, 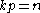 . There exist constants
. There exist constants 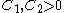 such that
such that

